Points of Concurrency in Triangles

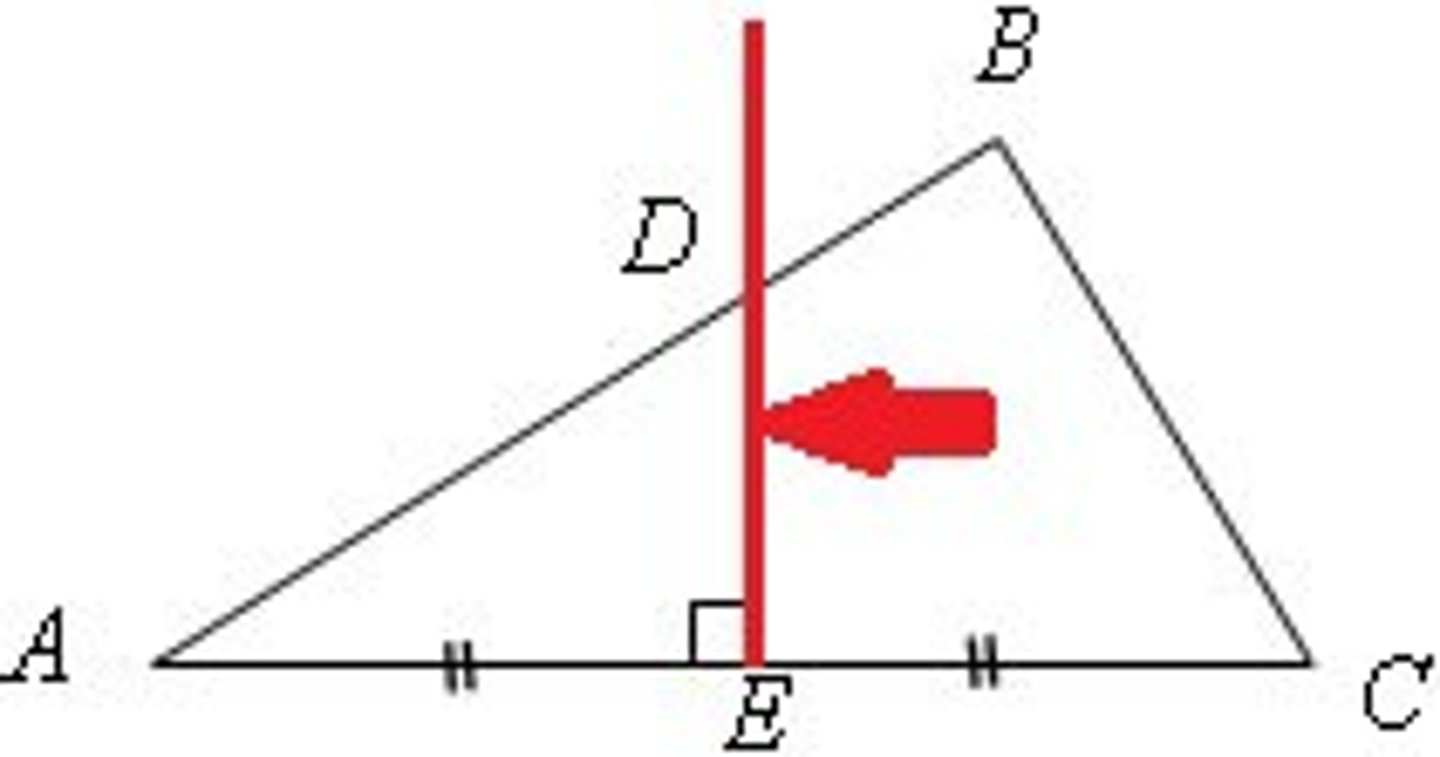
Perpendicular Bisector

A line segment that is perpendicular to a side of a triangle at its midpoint.

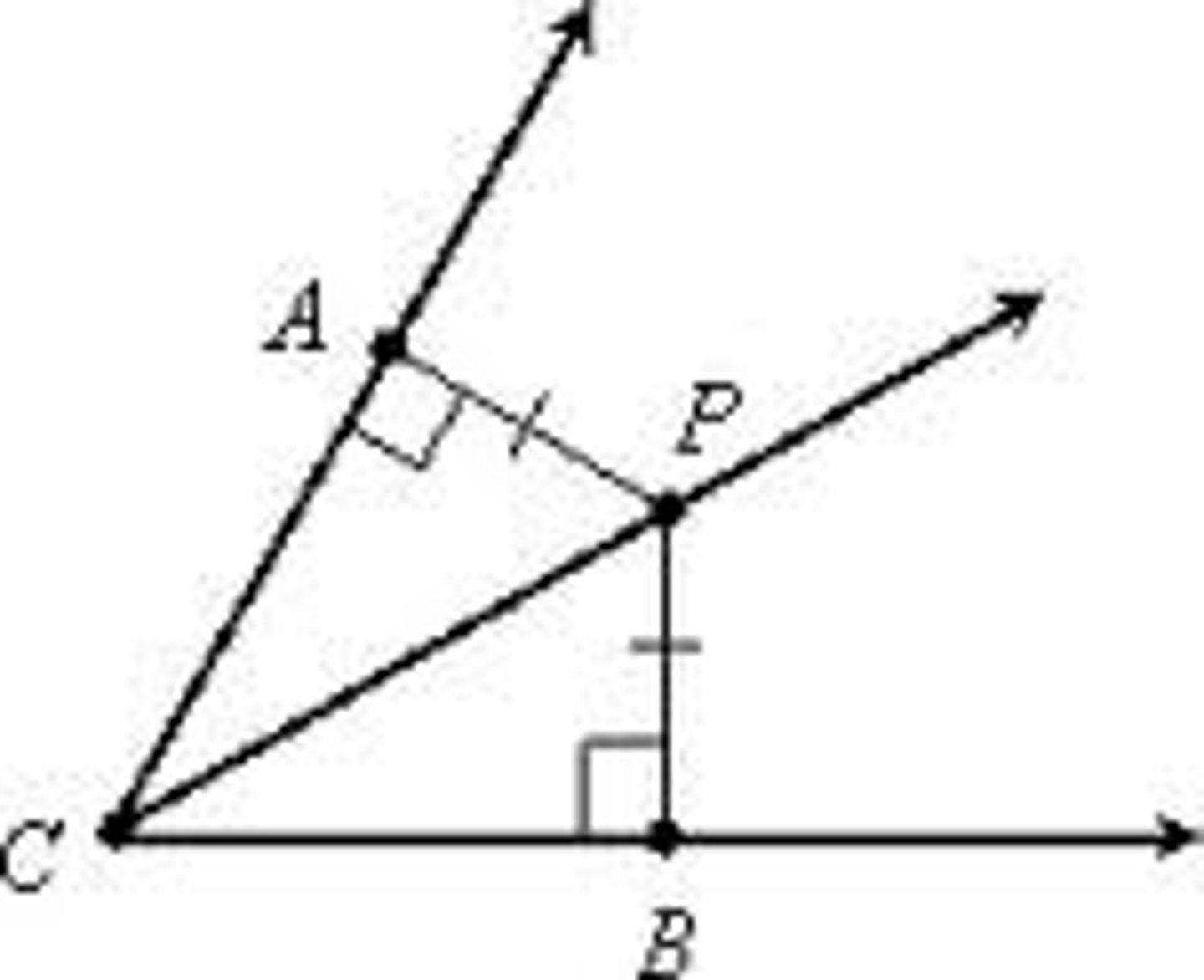
Angle Bisector

A line segment/ray that splits an angle into two congruent angles

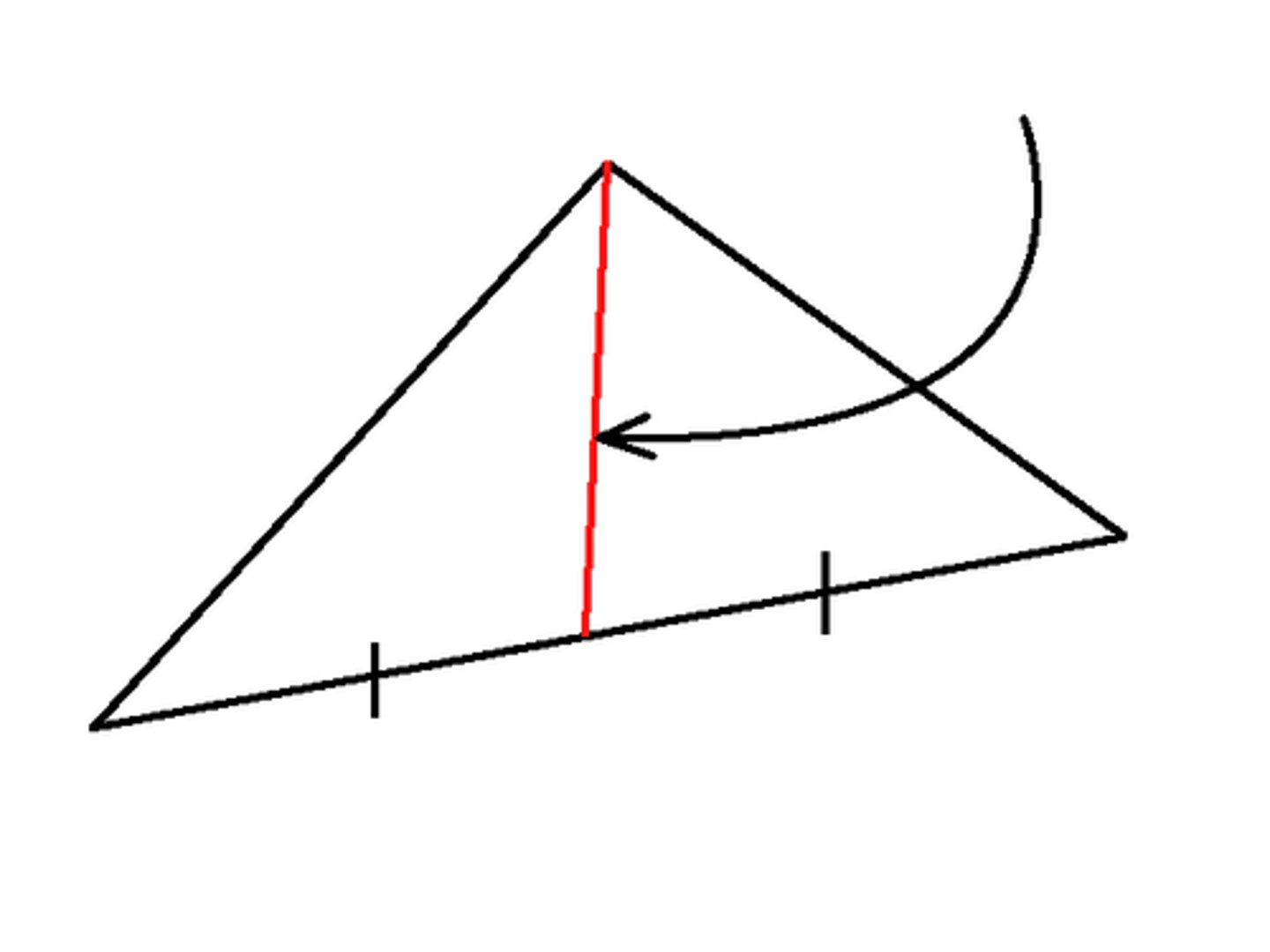
Median

A segment drawn from a vertex to the midpoint of the opposite side of a triangle

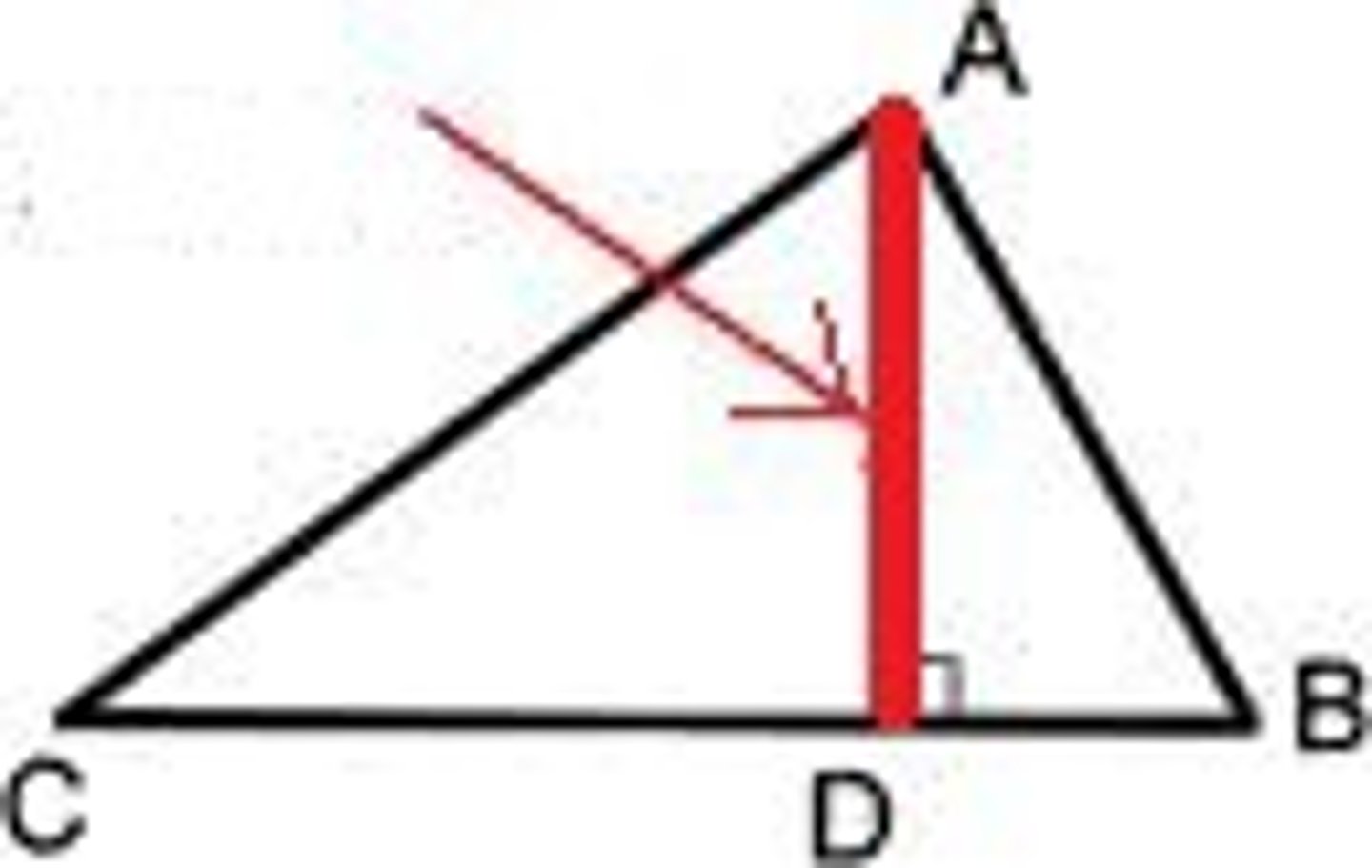
Altitude

A perpendicular segment drawn from a vertex to the opposite side of a triangle

What are the points of concurrency in triangles?

Circumcenter, Incenter, Centroid, Orthocenter

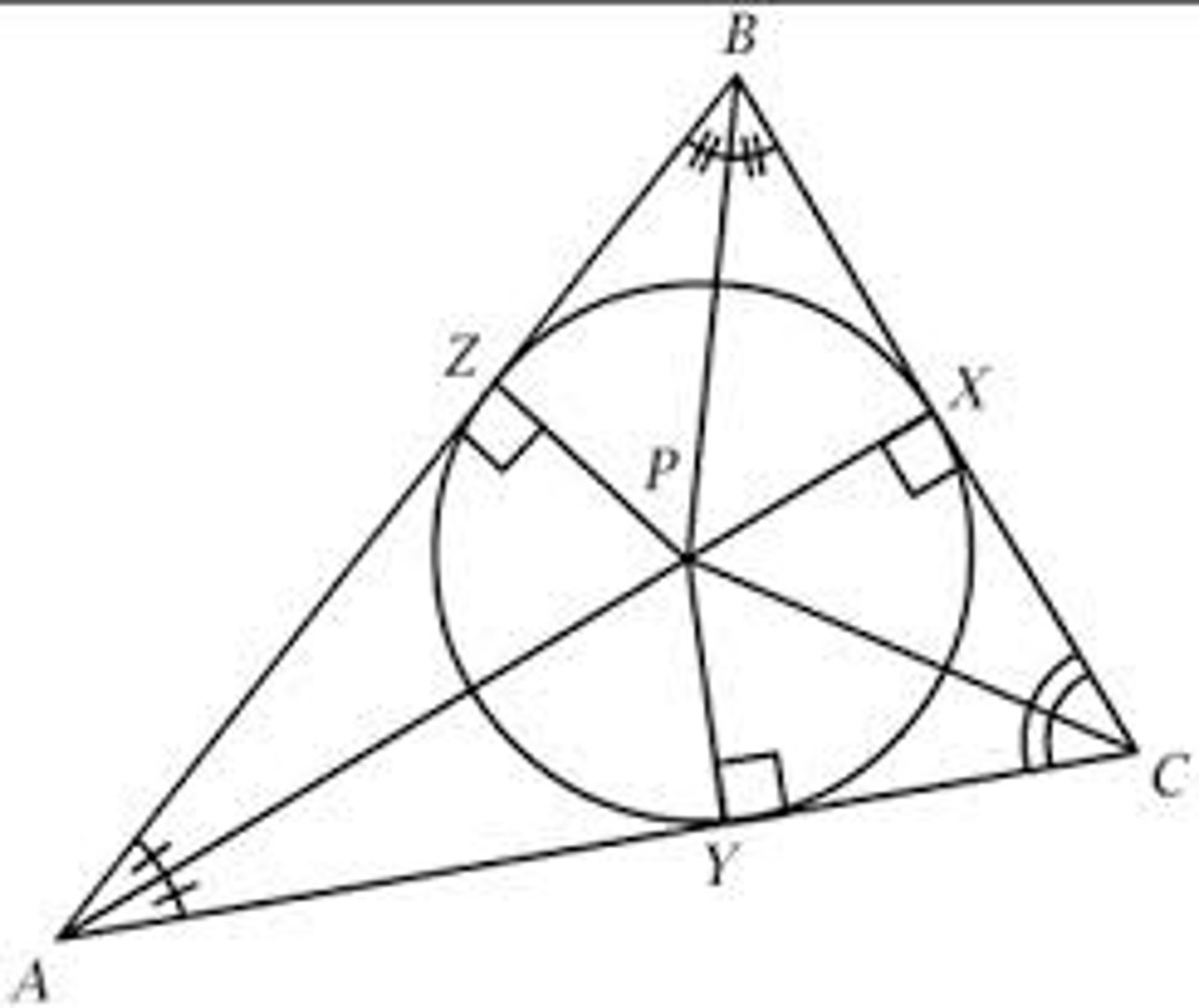
Circumcenter

Point where all 3 perpendicular bisectors intersect

Where can this be found: can be found on the inside, outside, and on the triangle

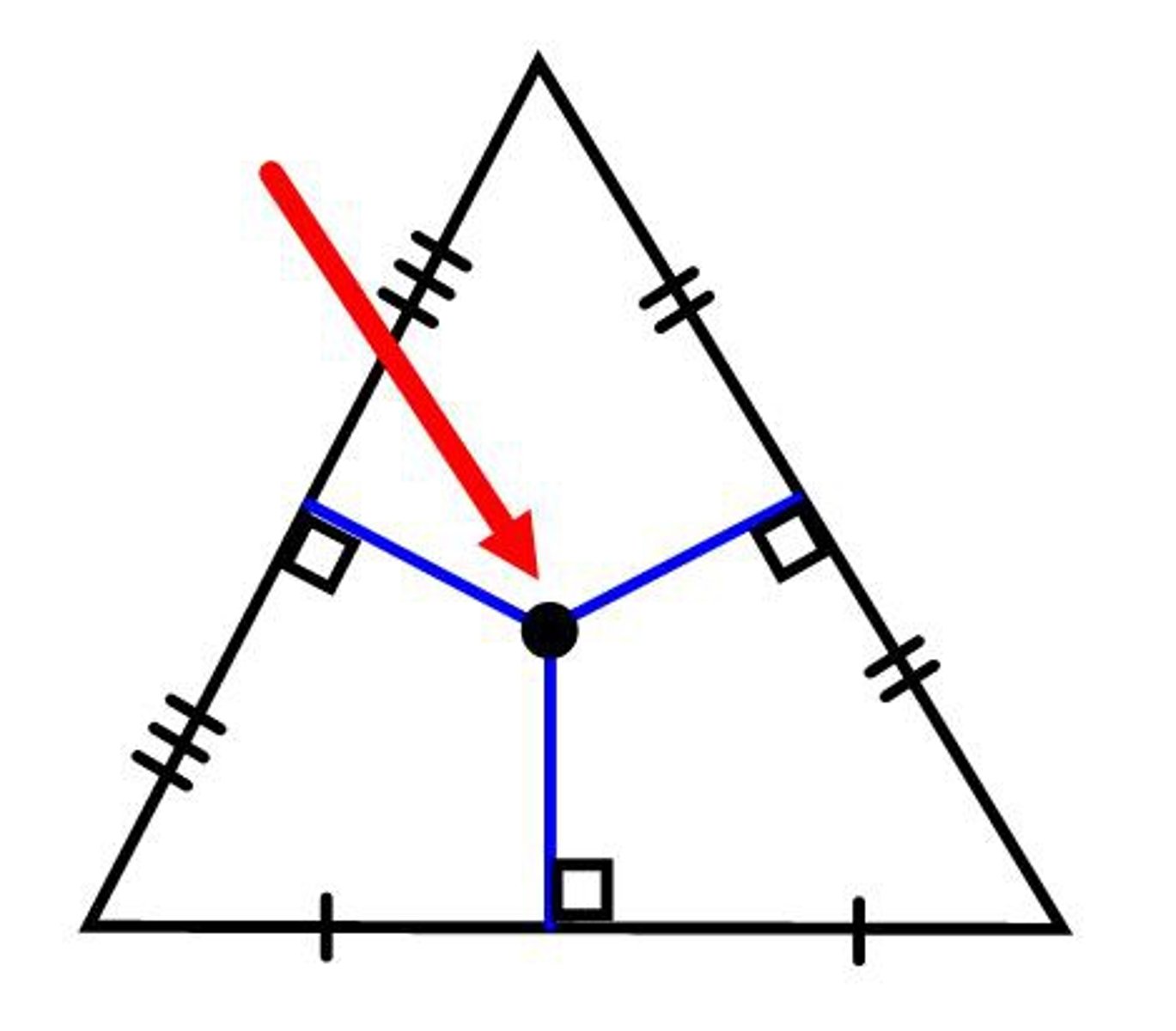
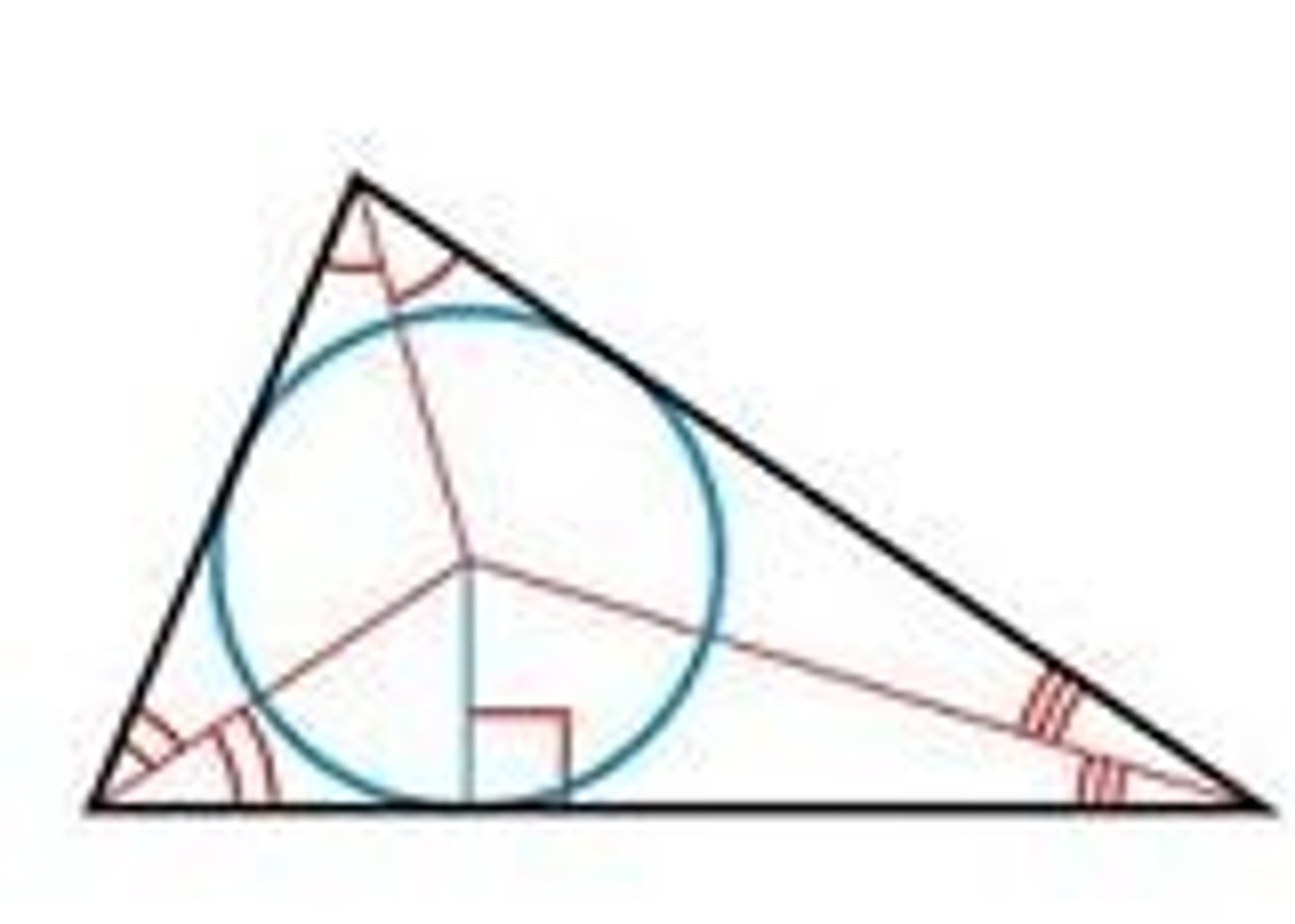
Incenter

Point where all 3 angles bisectors intersect

Where can this be found: can only be on the inside of the triangle

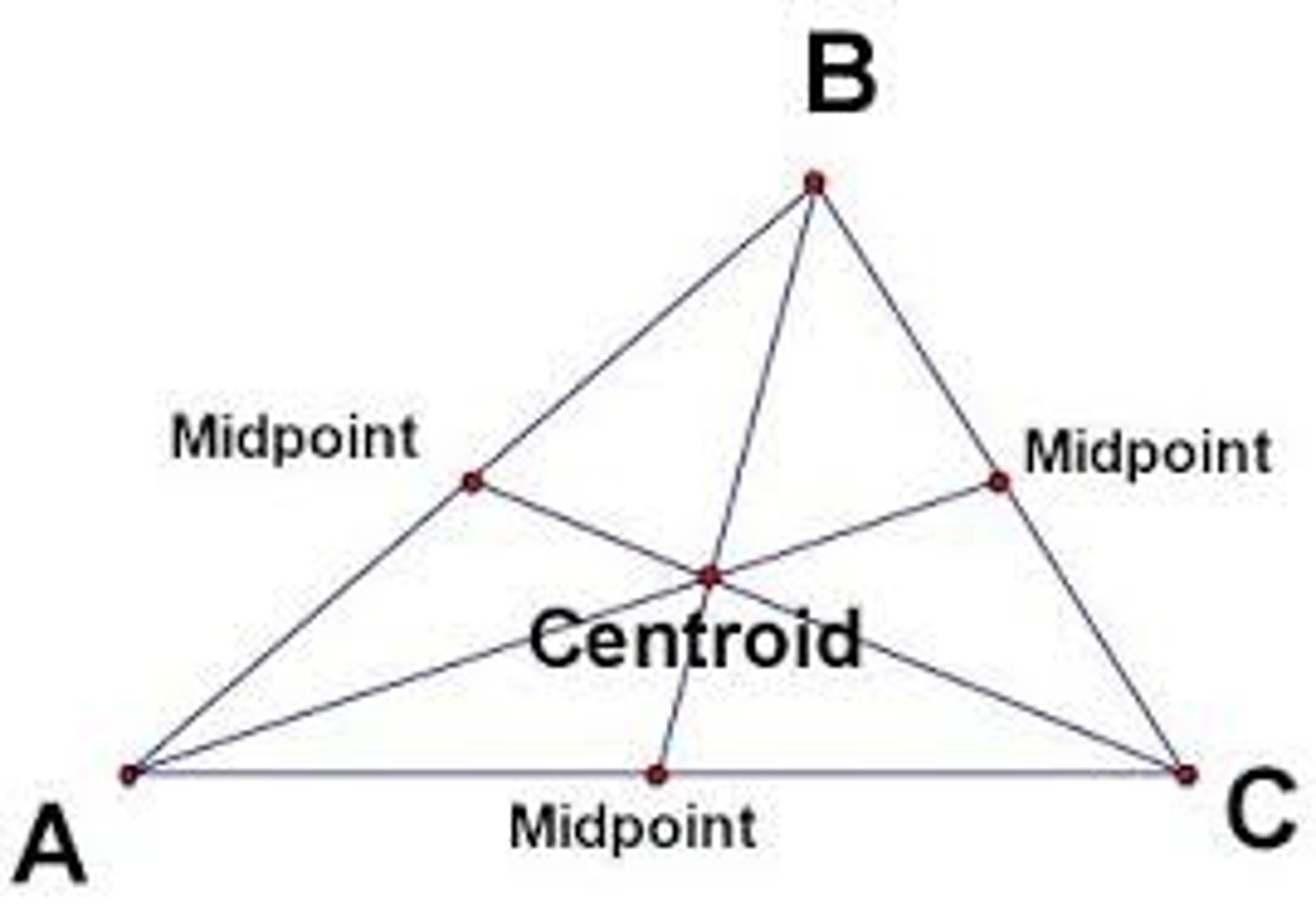
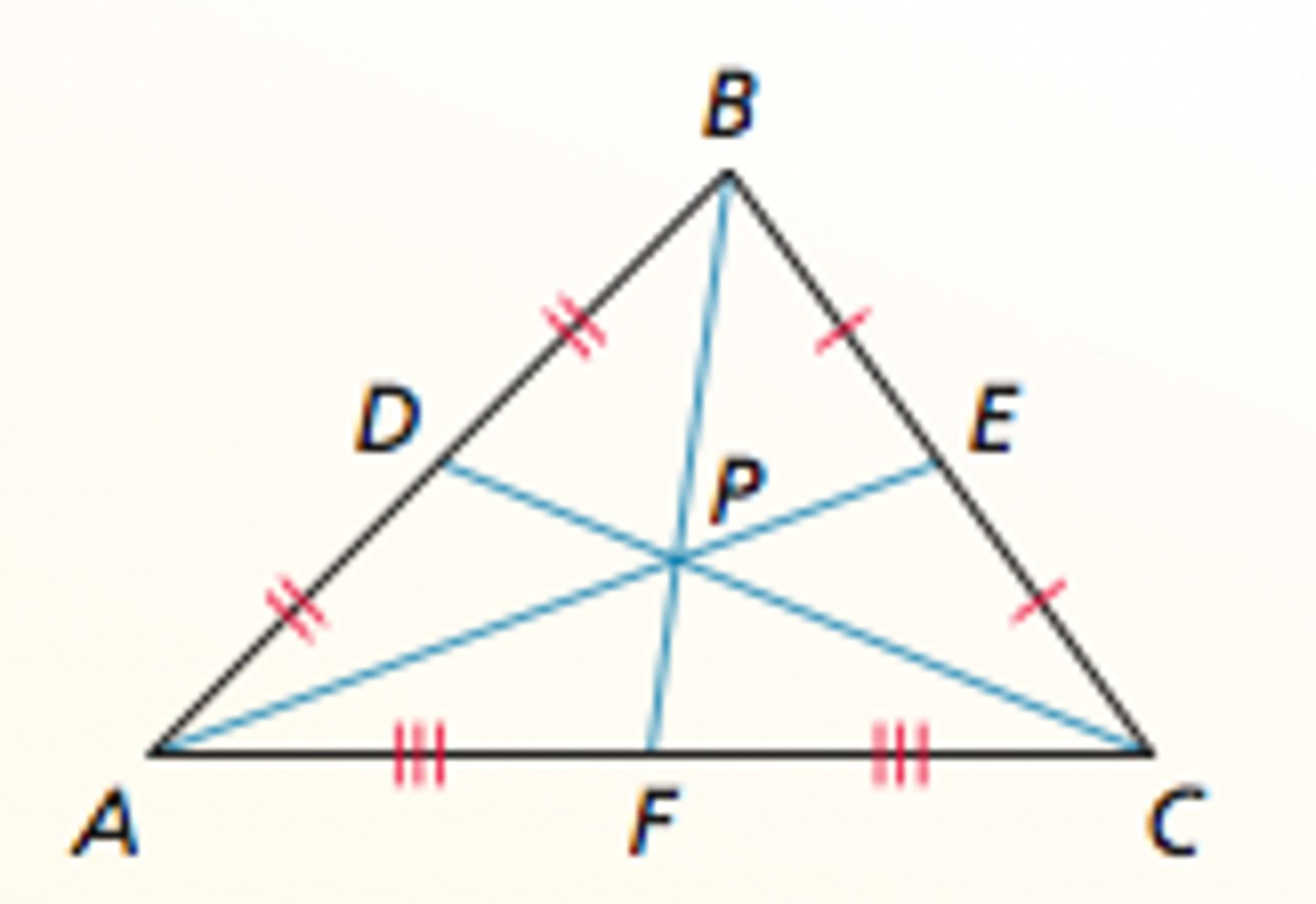
Centroid

Point where all 3 medians intersect

Where can this be found: can only be on the inside of the circle

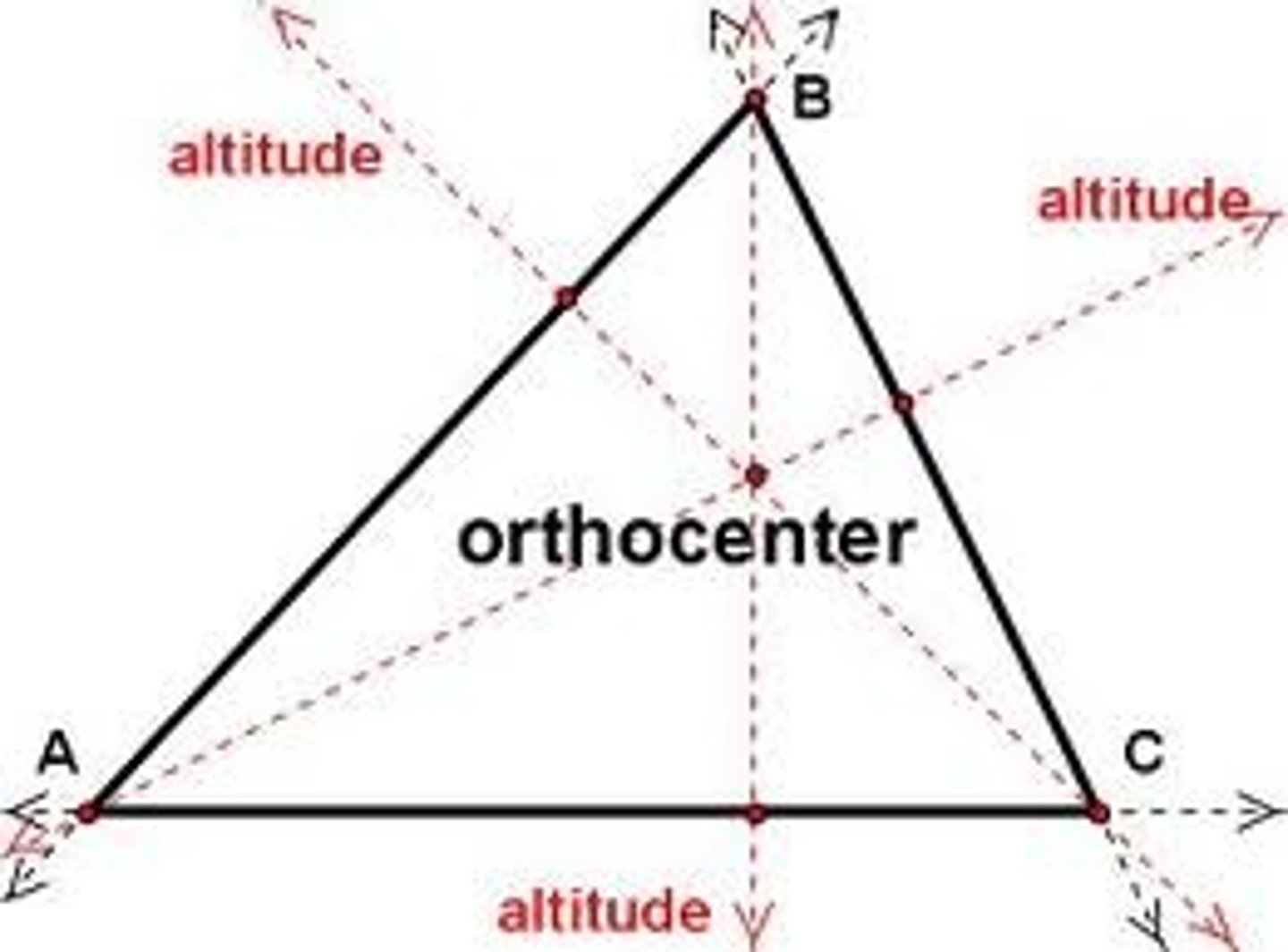
Orthocenter

Point where all 3 altitudes intersect

Where can this be found: can be in the circle, on the circle, or on the outside of the circle

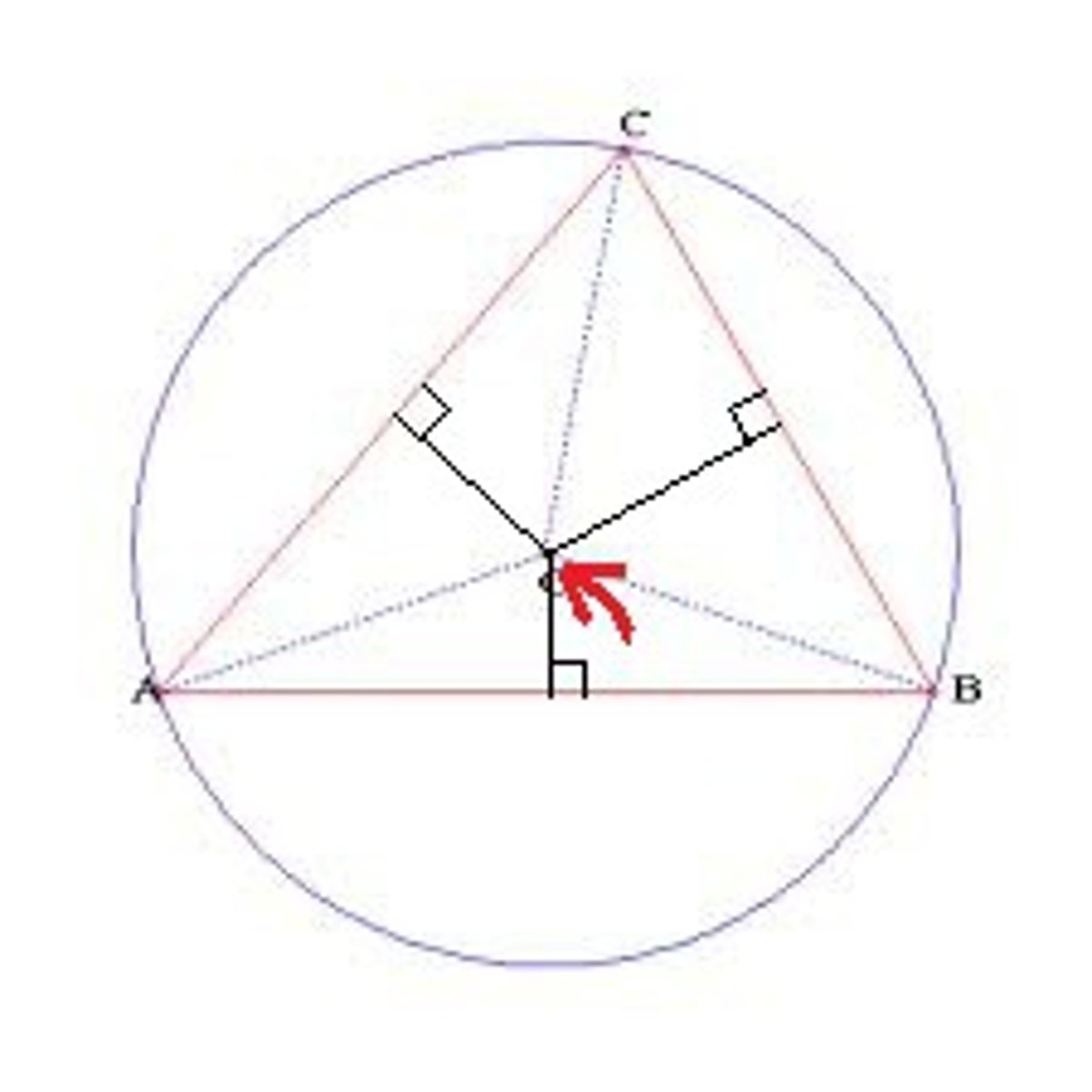
Special Properties of Circumcenter

Circumcenter is equidistant to all of the vertices

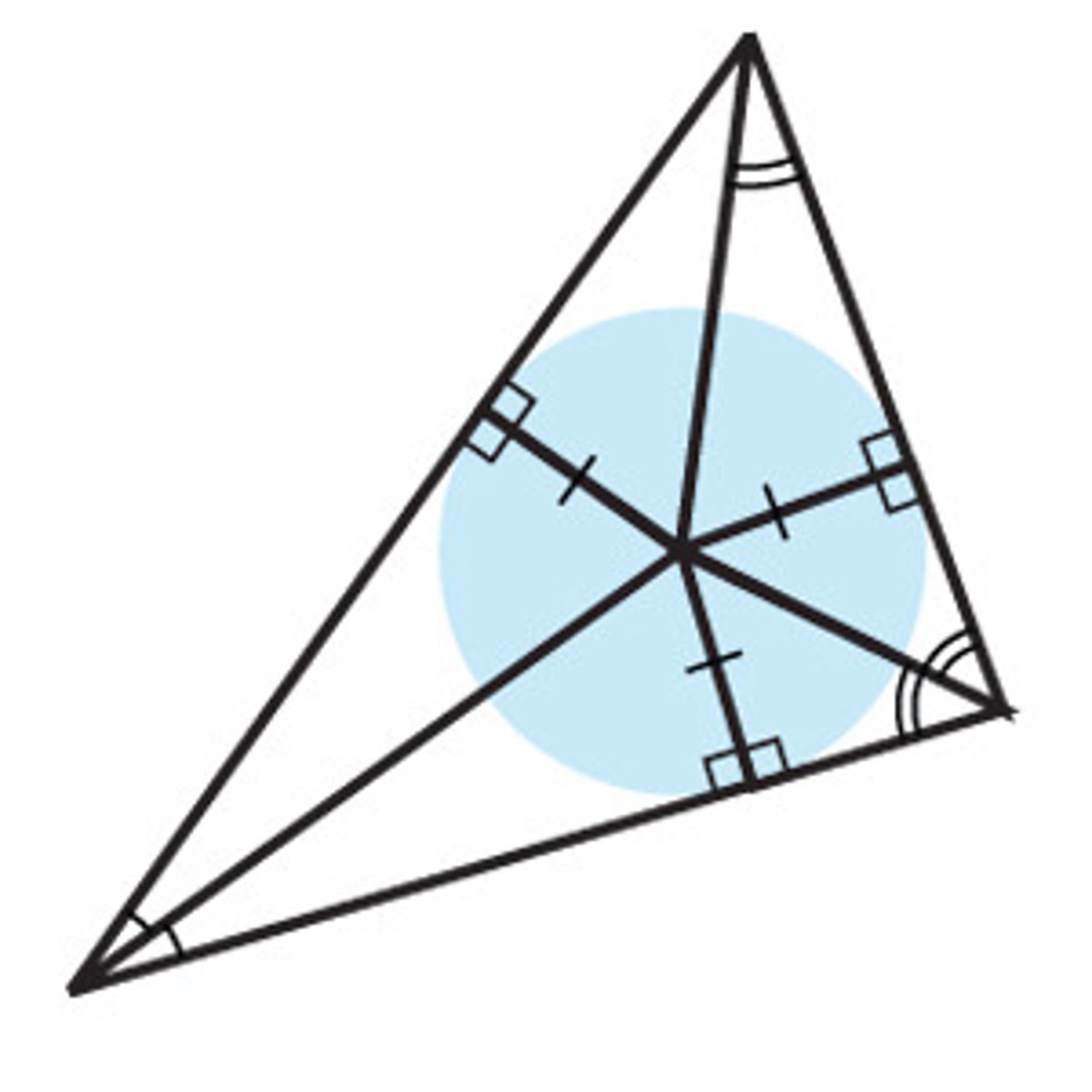
Special Properties of Incenter

Incenter is equidistant to all of the sides

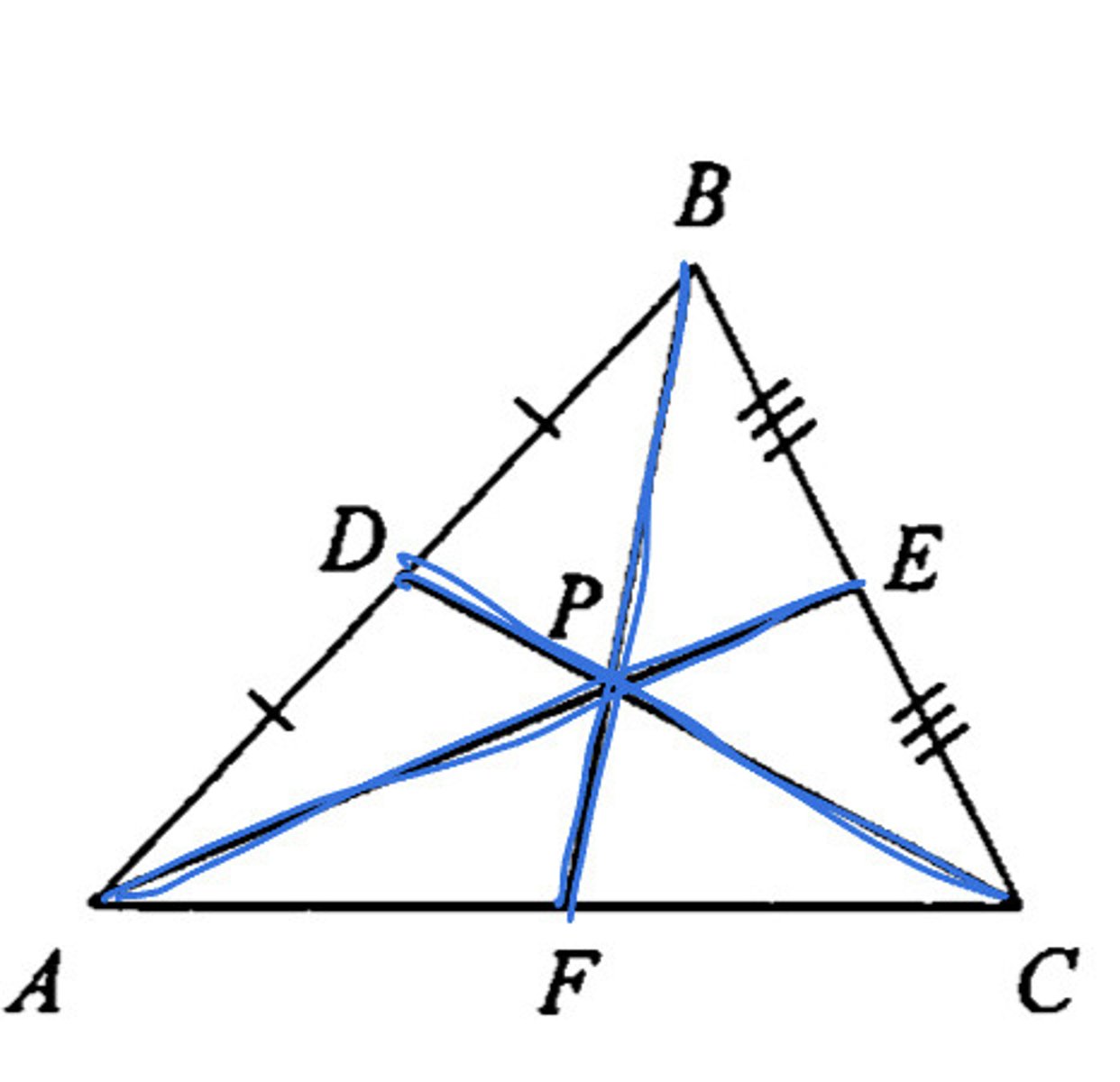
Special Properties of Centroid

1. Centroid-> vertex: 2/3(total) (long segment)

2. Centroid-> side: 1/3(total) (short segment)

3. Long short ratio

4. 2:1 ratio

Special Properties of Orthocenter

NO REALATIONSHIP

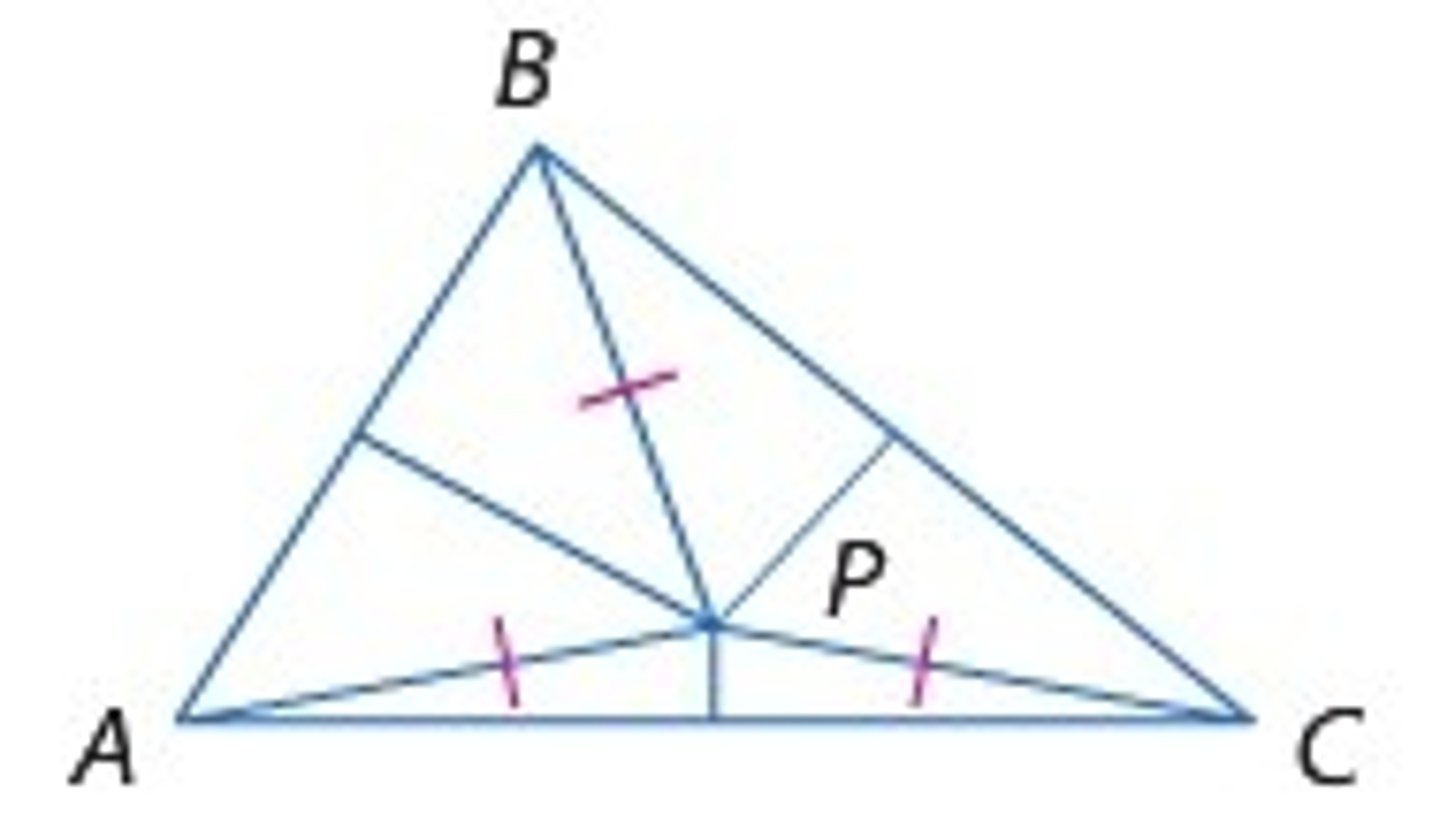
Examples of Circumcenter

Equidistant to all the vertices

Examples of Incenter

Equidistant to all the sides

Examples of Centroid

1. 2:1 ratio

2. Long segment: 2/3(total)

3. Short segment: 1/3(total)

Examples of Orthocenter

No relationship to show example problems