Linear Algebra Final: Terms and Practice

Vector

a matrix of size 1 x n or m x 1

s:= (s₁,…, s_n) (row vector)

or

x:=(x₁,…,x_m)^T (column vector)

Matrix

an m x n matrix is an array of numbers:

A:=

(a₁₁ a₁₂ … a_1n,

a₂₁ a₂₂ … a_2n

.

.

.

a_m1 a_m2 …a_mn)

What can solution sets contain?

they can be empty, 0, 1 thing, or infinitely many things

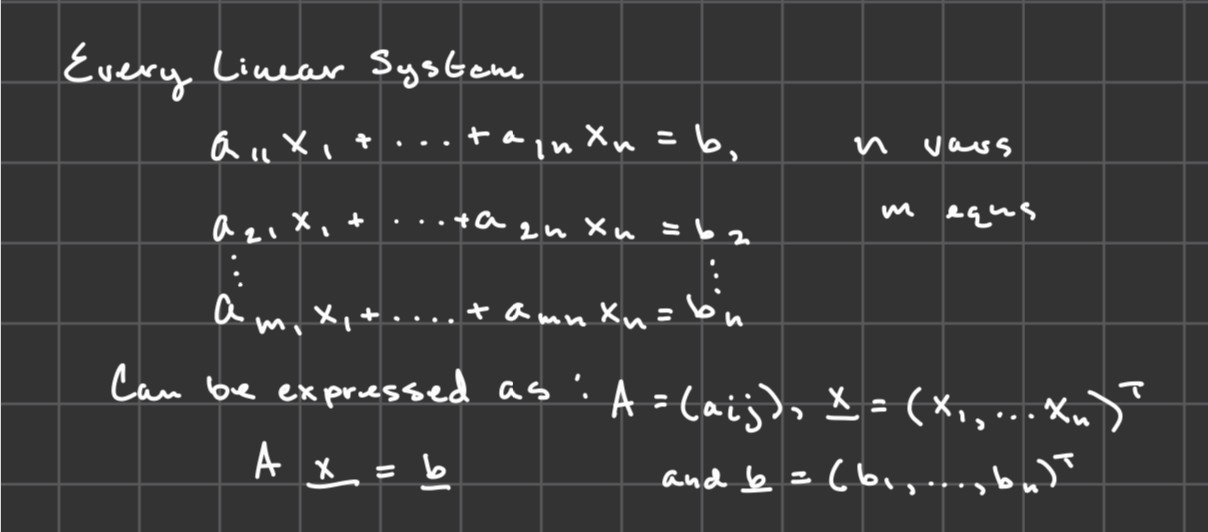
Matrix product/Dot product

If v = (v₁,…, v_n), and w = (w₁,…,w_m)^T are vectors, then the dot product v dot w := (v₁w₁ +…+v_nw_m) ∈R

For dot product v must have the same number of rows as w has columns or be a square matrix. vw and wv are not the same product.

Row Operation Rules

• Switch two rows

• Scale a row

• Replace a row with the sum of rows

For homogenous systems

-there is always at LEAST a trivial solution

-it is consistent (no empty rows/sets)

To find pivots and free variables

-put into REF (row eschelon form)

-if last column has no pivot, and there is a zero, the zero is the given free variable

Reduced Row Eschelon Form (RREF)

1. Any non-zero row comes before all zero rows

2. Any non-zero row has first entry 1, and zeros above and below leading 1

3. leading ones must stagger to the right, creating stair step

RREF U thm

Every matrix A can be put into RREF U by row operations and moreover U is unique. Thus, solutions to Ax=0 and Ux=0 are the same.

For inhomogeneous systems such as Ax=b, b≠0, there are 2 ways to solve

1. Augmented matrix

2. Transfer Principle

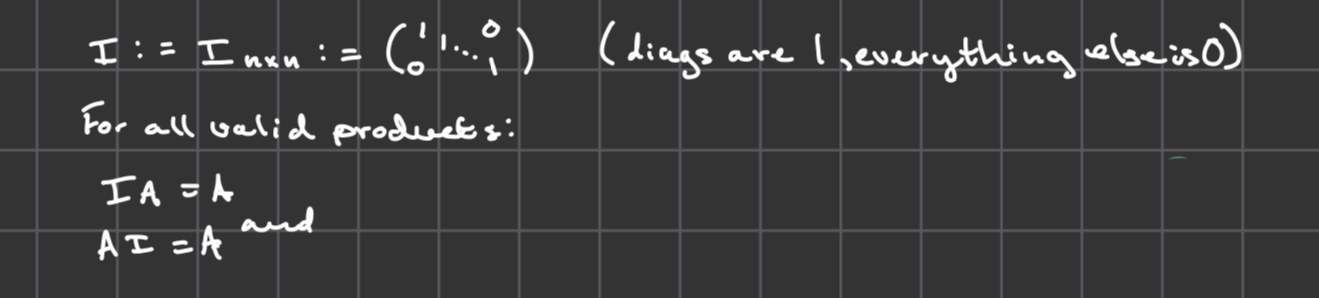
A square matrix A is invertible if there is a matrix A^-1 such that:

A^-1A= I

AA^-1= I

If A= (a b, c d) then,

A^-1 = (1/ad-cb)(d -b, -c a)

A is not invertible if ad-cb=0

If A in invertible, any system Ax=b has one unique solution: x= Ix = A^-1Ax = A^-1b.

So, a square matrix A is invertible iff its RREF is U=I.

Transfer Principle

Let A be a matrix and S_h : {s_h: As_h = 0} the set of solutions to Ax = 0. For any b with a particular solution s_p to Ax = b, i.e. As_p=b, the solutions to Ax=b is {s_p + s_h: s_h∈ S_h}

Elementary matrices: 3 types

1. Pij: identified as an identity matrix with ij rows swapped

2. (i≠j), 3. (i=j), Eij (α): identified as α∈R, places α in the identity matrix at slot (i,j)

Subspace of a vector space

If it meets these properties, the subset is a subspace. Use generic elements to prove that it is one, and specific elements (witnesses) to prove that it is not! (If any of the functions are non-linear, it is more than likely not a subspace)

Linear Combinations

Fix v₁, … ,v_n in R^α.

A linear combination of v₁, …, v_n is a vector of the form c₁v₁+ …+ c_nv_n for c₁,…,c_n ∈ R.

Defn Spanning set

For β:={v₁,…,v_x} ∈R^d, a finite set. We set

Span(β):={c₁v₁+ …+ c_nv_n: c₁,…, c_n∈R} ⊆R^d, the set of all linear combinations of v₁,…, v_n.

• Span(β) is always a subspace

• Every subspace V ⊆ R^d, V=Span(β), for any finite set β

We call β a spanning set for V.

Null space

Null(A):={x ∈ Rⁿ: Ax=0} ⊆Rⁿ

Is the solution to the homogeneous system, called the Null Space of A.

• Null(A) is always a subspace

• Let s₁, s₂ ∈ Null(A) generic α∈R.

  • As₁=0, As₂=0 and A(s₁ + s₂)=0

  • A(αs₁) = α(As₁)= α * 0 = 0.

Linear independence and Basis Definition

Fix β = {v₁,…,v_n} ∈R^d.

We call β linearly independent provided:

• c₁v₁+ …+ c_nv_n=0 => c₁=0, c₂=0,..., c_n=0

• If β is not linearly independent, we say β is linearly dependent.

We call a set β a basis for a subspace V if:

• β is a spanning set for V

  • there are c₁,c₂, ∈ R such that c₁b₁+ c₂b₂=b

    • iff Ac=b i.e. Ax=b has a solution

• β is linearly independent

  • iff Ax = 0, A=(—b₁—,…, —b_n—)^T

dim(V) is the same size as any basis, b_n ⊆ V

dim(R^d) = d,

as R^d = Span{e₁,…, e_d}.

Thus any set β with #β>d cannot be linearly independent, and #β<d cannot be a spanning set for R^d.

Moreover, #β=d, then β is linearly independent iff β is a spanning set for R^d.

Three important subspaces attached to an m x n matrix A:

1. Null Space

   Null(A) := {x ∈ Rⁿ: Ax=0} ⊆ Rⁿ

   dimNull(A):= nullity(A) [num of free vars!!]

2. Row Space/Rank

   Row(A):= Span(rows of A) ⊆ Rⁿ

   Rank(A) = dimRow(A)

3. Column Space

   Col(A) = Span(cols of A)

Rank- Nullity Theorem

For A, an m x n matrix,

Rank(A) + nullity(A) = n = number of columns

β coordinate of v definition

if V is a subspace and β = {b₁,…,b_n} is a basis for V,

every vector v ∈ V, has a unique linear combination (c₁, c₂,…,c_n)^T such that

v= b₁c₁+…+b_nc_n, we call

[v]_β:= (c₁, c₂,…,c_n)^T the β coordinates of v.

Change of basis: is a matrix

Fix V a vector space with basis’ β, β’.

For any vector v ∈ V, we can calculate

[v]_β ∈R^d

[v]_β’ ∈R^d.

There is an invertible d x d matrix(change of basis matrix):

A_β→β’ such that

A_β→β’[v]_β=[v]_β’.

(therefor [v]_β=A^-1_β→β’[v]_β’)

So

A^-1_β→β’=A_β’→β.

Injective

β is linearly independent

Surjective

β is a spanning set for V

Bijective

Injective and surjective

Linear Transformation definition

Let V, W be two vector spaces. A Linear Transformation is a function L: V→W such that

1. L(v₁ + v₂) = L(v₁) + L(v₂)

2. L(αv₁) = αL(v₁)

   For all α ∈ R, v₁, v₂ ∈ V.

Linear Operator definition

If V = W, we call a linear transformation L: V→V a linear operator

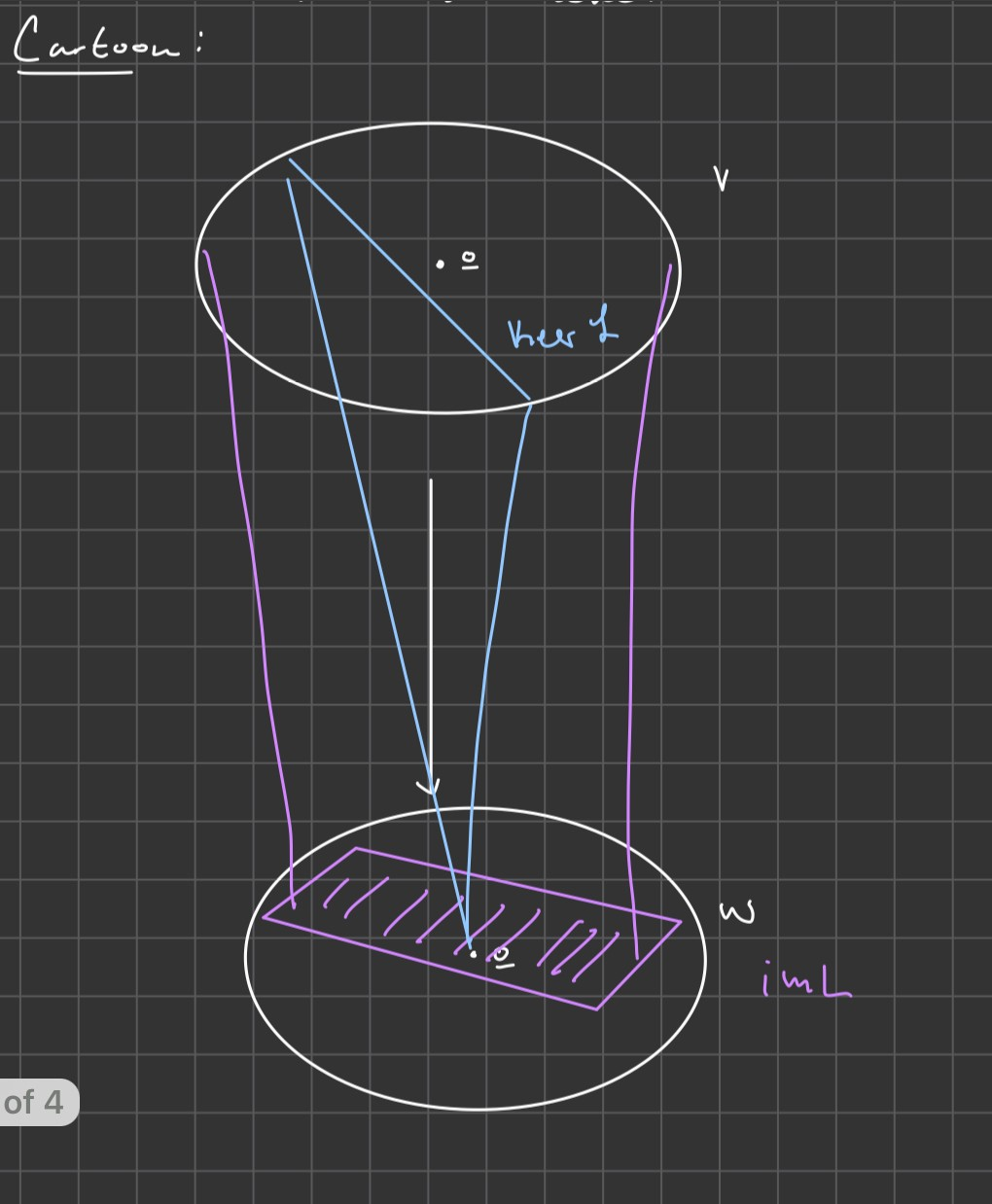
Kernal of L and Image of L-

2 important subspaces attached to a linear transformation

Ker L := {v ∈ V: L(v) = 0} ⊆ V

• Information lost by L

Im L ;= {w ∈ W: there is v ∈ V, L(v) = w} ⊆ W

• What L touches

Correspondence for any linear transformation: L: V →W:

Pick basis β_v for V, d_v := dimV; β_w for W, d_w := dimW,

then correspondance:

[—]_βv

V→R^dv

v |→ [v]_βv

[—]_βw

W→R^dw

w |→ [w]_βw.

Under these identifications,

as

[L(v)]_βw = [L]_βv^βw * [v]_βv.

So. this identifies:

kerL ∈ V with Null([L]_βv^βw) ∈ R^dv

and

imL ∈ W with Col([L]_βv^βw) ∈ R^dv

By definition L is surjective iff imL = W, and L is injective iff kerL = {0}.

L(v₁) = L(v₂) iff

L(v₁) - L(v₂) = 0

= L(v₁ - v₂),

So v₁ - v₂ ∈ kerL

For each L we obtain a #, vol(L)

Systematic process to find

vol[L] from [L]_βv^βw. This is called the determinate.

Thm: for L : V → W linear transformation:

|det [L]_βv^βw| = vol(L) for any choice of basis.