Linear Algebra Prelim 1 stuff

linear combination (definition)

adding vectors of different weights creates a new vector. we say that this new vector is a linear combination of the added vectors.

the weights can include zero

this will tie into span

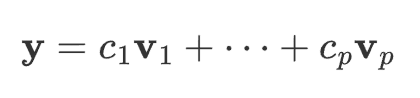
span (defintion, vector b in span{v1,…vp} mean? geometric description, linear combination)

definition: span{v1,…vp} is the collection of all vectors that can be written in the form c1v1 + c2v2 + …. +cpvp. c are the scalaras.

vector b is in Span {v1, …, vp}?: we have to find whether the vector equation has a solution. we find if the augmented matrix [ v1 … vp b] has a solution.

geometric description:

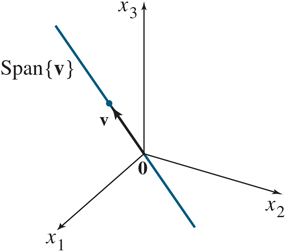
• with vector v in R³ , span{v} is the set of all scalar multiples of v, which is the set of all points on the line in R³ through v and 0.

• span{u, v} , if the vectors aren’t multiples of each other, this will create a plane in R³ that contains u, v, and 0.

linear combination: span is really all linear combinations of something

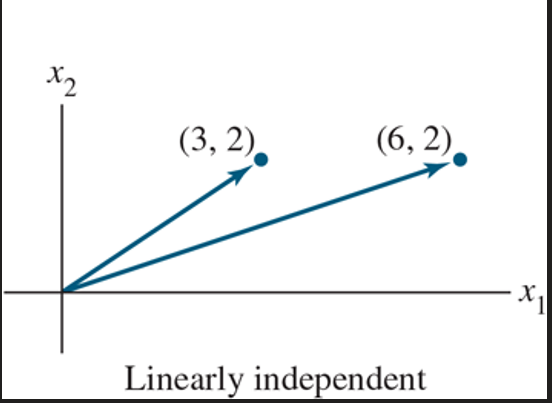
linearly independent (definition for vectors, definition for matrix A, geometric description, what if there are more vectors than entries?)

definition vectors: an indexed set of vectors {v1, …, vp} in R^n is said to be linearly independent if the vector equation

x1v1 + x2v2 + … + xpvp = 0

has only the trivial solution.

can also add that the two vectors are not multiples of each other. two vectors are not a linear combination of the other vector.

definition matrix A: the columns of a matrix A are linearly independent if and only if the equation Ax = 0 has only the trivial solution. This means that there are no free variables in the reduced augmented matrix.

geometric description: its like two different vectors that aren’t on top of each other

vectors vs entries:

if columns > rows, then the set is linearly dependent. cuz theres gotta be a free variable.

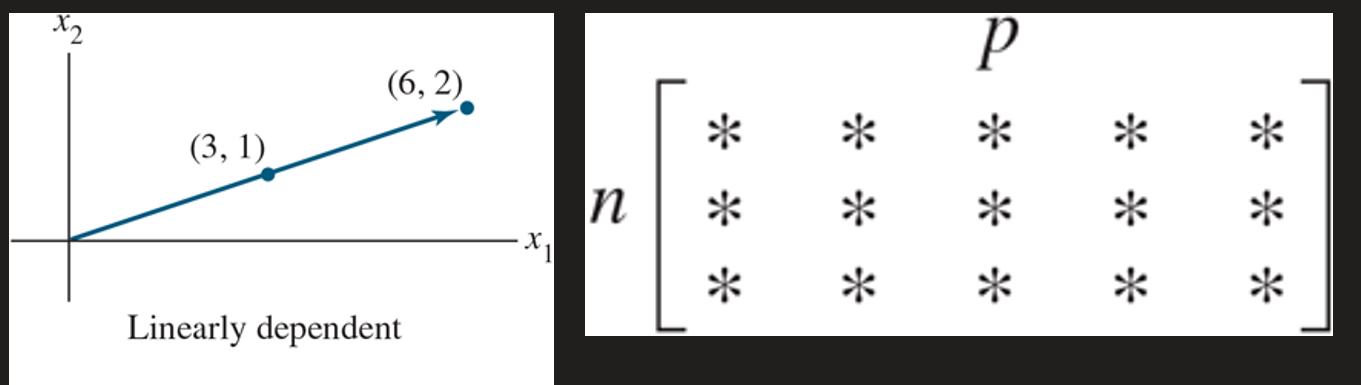
linearly dependent (definition for vectors, geometric description, vectors vs entries)

definition: the set {v1, …, vp} is said to be linearly dependent if there exists weights c1,…cp, not all zero, such that:

c1v1 + c2v2 + … + cpvp = 0

note: zero vector is always linear dependent

a set of two vectors {v1, v2} is linearly dependent if at least one of the vectors is a multiple of the other.

a set of two vectors are linearly dependent if they’re linear combinations of the other. (BUT NOT FOR THE ENTIRE SET), also has to be in span.

geometric description: basically, the vectors are placed right on top of each other (so romantic!!! help)

vectors vs entries: if the vectors (columns) > than entries (rows), then the set is linearly dependent. cuz there’s free variables.

free variable

no constraints to the value of the variable

onto (definition,

a mappings T: R^n → R^m is said to be onto R^m if each b in R^m is the image of at least one x in R^m.

there is a pivot in every row

one-to-one (definition

a mapping T: R^n → R^m is said to be one-to-one if each b in R^m is the image of at most one x in R^n.

there are no free variables

invertible matrix

matrix multiplication (square, non-square)

A^T (Transpose)

identity matrix

invertible matrix formula: 2×2

basic transformations:

• reflection across x1 axis

• reflection across x2 axis

• reflection across x2 = x1

• reflection across x2 = -x1

• reflection across the origin

• in a 2×2 matrix, tell me which square corresponds to what entry, and what coordinate (x/x1, y/x2)

Reflection across x1 axis:

1 0

0 -1

Reflection across x2 axis:

-1 0

0 1

Reflection through the line x2 = x1

0 1

1 0

Reflection through the line x2 = -x1

0 -1

-1 0

Reflection through the origin

-1 0

0 -1

in a 2×2 matrix, tell me which square corresponds to what entry, and what coordinate (x/x1, y/x2)

a b

c d

a: 1st entry x coordinate

b: 1st entry y coordinate

c: 2nd entry x coordinate

d: 2nd entry y coordinate

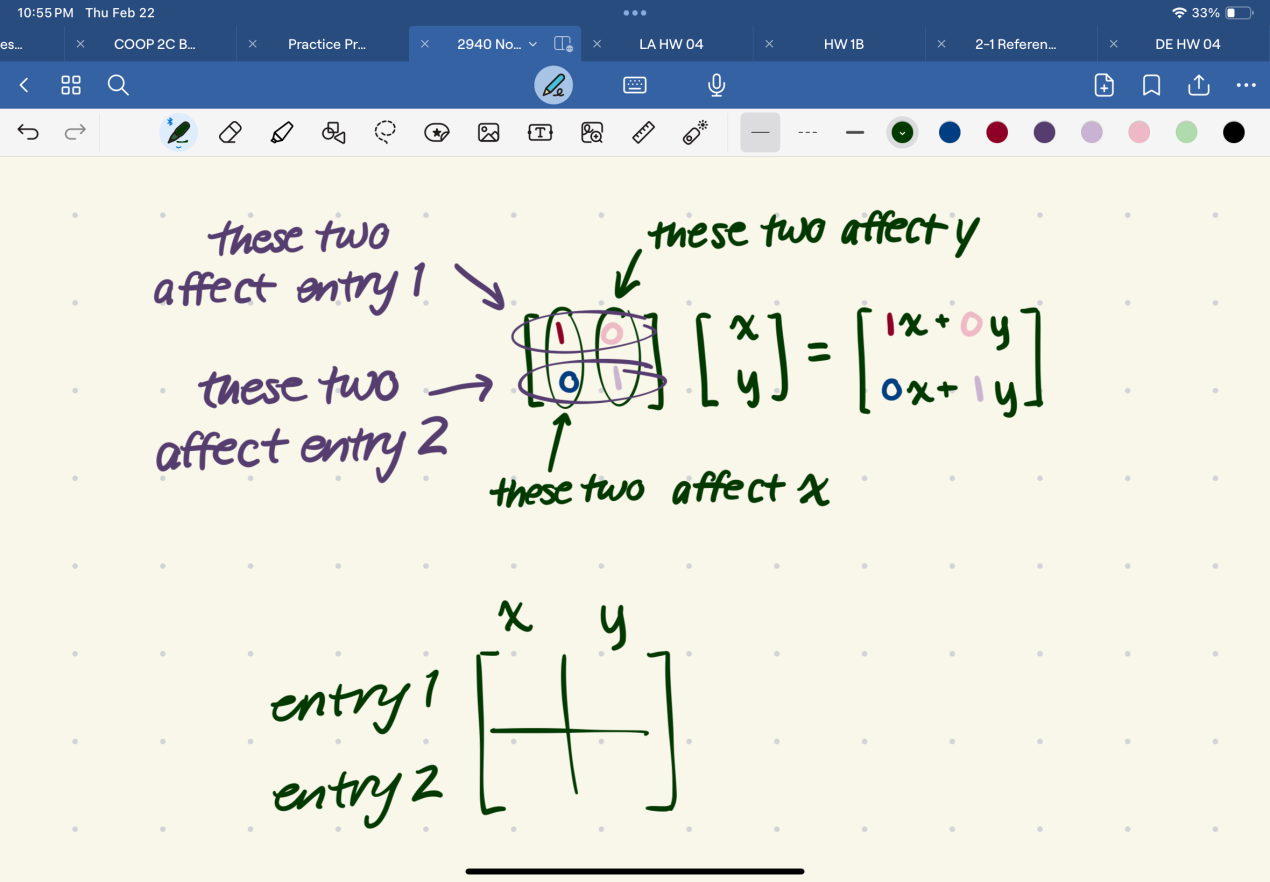
mapping (TBD)

homogeneous system (definition, when does have nontrivial solution, geometric description)

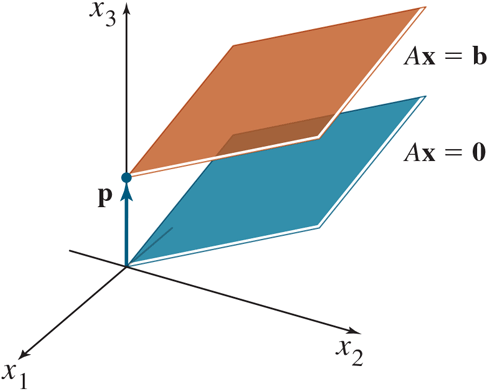
defintion: A system of linear equation is said to be homogeneous if it can be written in the form Ax = 0, where A is an m x n matrix and 0 is the zero vector in R^m. Such a system Ax = 0 always has at least one solution, namely x = 0 (the zero vector in R^n). The zero solution is usually called the trivial solution.

So the important thing we want to figure out is if this homogeneous has a nontrivial solution.

• If and only if the system has at least one free variable,

  then the homogeneous solution has a nontrival solution

Geometric description: a solution set is a line through 0 in R³

parametric vector form (definition, geometric description)

defintion: an explicit description of the plane as the set spanned by u and v can be written as a parametric vector form.

x = su + tv (s, t in R)

• can use this to write solutions to nonhomogeneous linear system

geometric description: if we have a solution to Ax = b, say p, then the solution set of Ax = b is a solution of Ax = 0 + p (Ax = 0 translated p)