Linear Algebra Prelim 1 stuff

Homogeneous System:

A system of linear equation is said to be homogeneous if it can be written in the form Ax = 0, where A is an m x n matrix and 0 is the zero vector in R^m. Such a system Ax = 0 always has at least one solution, namely x = 0 (the zero vector in R^n). The zero solution is usually called the trivial solution.

So the important thing we want to figure out is if this homogeneous has a nontrivial solution.

• If and only if the system has one free variable, it is homogeneous.

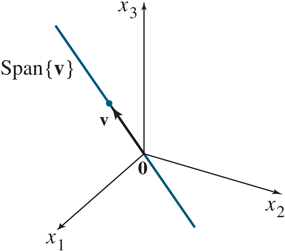
Geometric description:

• solution set is a line through 0 in R³

Parametric Vector Equation:

• an explicit description of the plane as the set spanned by u and v can be written as a parametric vector form.

  x = su + tv (s, t in R)

• can use this to write solutions to nonhomogeneous linear system

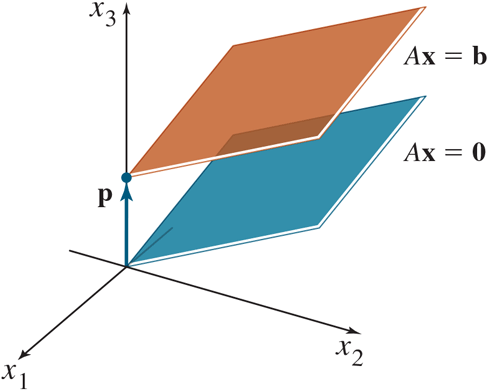
geometric description:

if we have a solution to Ax = b, say p, then the solution set of Ax = b is a solution of Ax = 0 + p (Ax = 0 translated p)