Chapter 3: Motion

Physics AS Level - OCR Gateway A completed ♡

Equation for speed with the units

speed (ms^-1) = distance (m) / time (s)

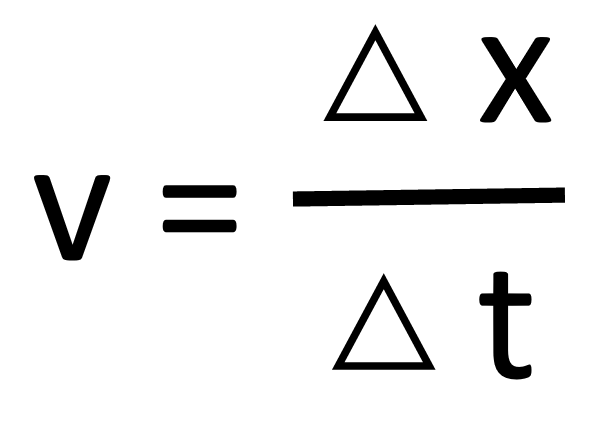
Definition of speed

Rate of change of distance

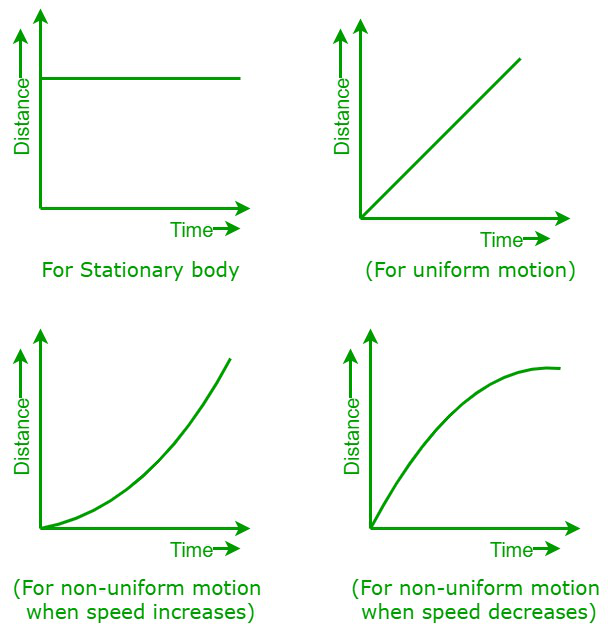
The x-axis and y-axis on a distance-time graph

x-axis: Time (s)

y-axis: Distance (m)

How are:

• Stationary objects

• Objects moving at a constant speed

• Objects with varying speed

portrayed on a distance-time graph?

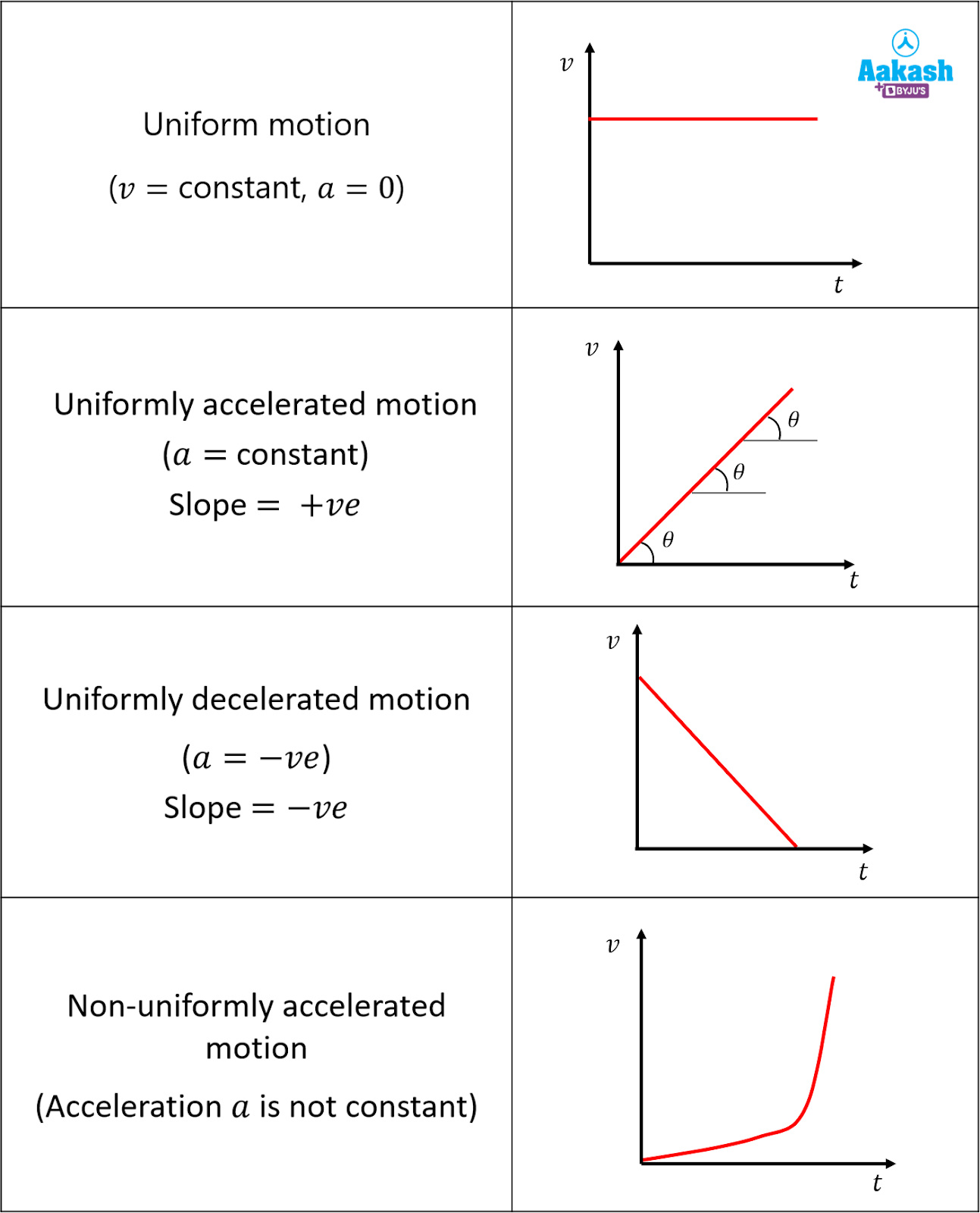
Stationary objects: horizontal line

Constant speed: sloping straight line

Varying speed: curved line

Instantaneous speed

The speed at any given point in time

Finding the instantaneous speed on a distance-time graph

• Draw a tangent

• Calculate the gradient of the tangent = speed

How is the acceleration found on a speed-time graph?

The gradient

How is the speed found on a distance-time graph?

The gradient

How is the distance found on a speed-time graph?

Area under the graph

How is the velocity found on a displacement-time graph?

The gradient

Equation for velocity with units

velocity (ms^-2) = change in displacement (m) / time (s)

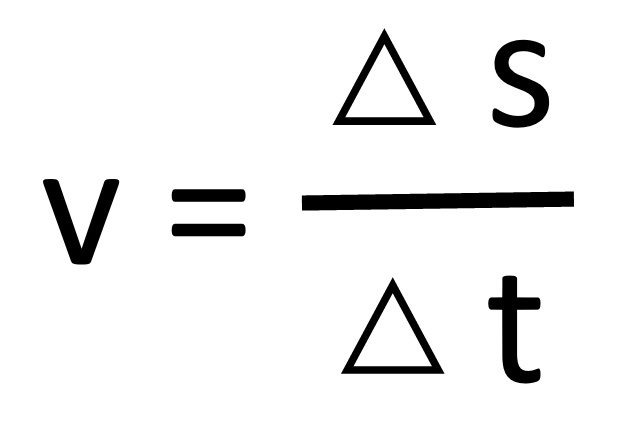
Definition of velocity

Rate of change of displacement

Equation for acceleration with units

acceleration (ms^-2) = change in velocity (ms^-1) / change in time (s)

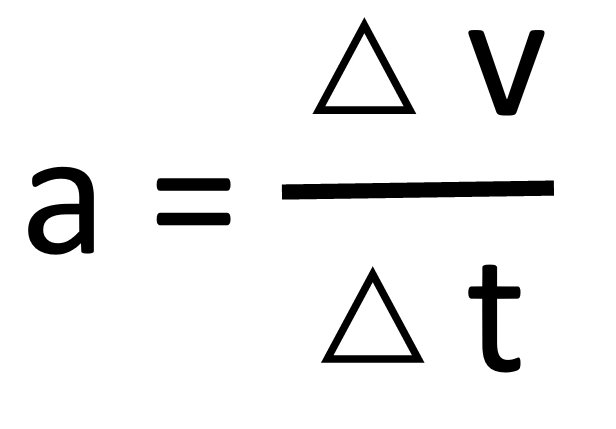
Define acceleration

Rate of change of velocity. Is a vector quantity.

How are:

• Stationary objects

• Objects moving at a constant velocity

• Objects with varying velocity

• Objects with increasing / decreasing velocity

portrayed on a velocity-time graph?

Stationary objects: horizontal line along the x-axis

Constant velocity: horizontal line not on the x-axis

Varying velocity: curved line

Increasing velocity: straight line +ve gradient

Decreasing velocity: straight line -ve gradient

What is the area under a velocity-time graph?

Distance / displacement

The distance of a non-linear velocity-time graph

Count the squares under the graph - only if the majority is under the curve

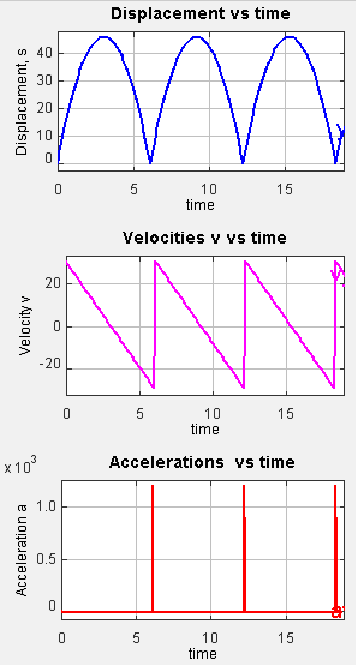
Draw a these graphs for a bouncing ball:

• displacement-time graph

• velocity-time graph

• acceleration-time graph

What are SUVAT equations used for?

constant acceleration

What does

S U V A T

stand for?

S displacement
U initial velocity
V final velocity
A acceleration
T time taken for the change in velocity

If an object starts from rest, what is the initial velocity / time taken for the change in velocity?

u = 0

t = 0

If an object’s initial velocity isn’t mentioned, what is the initial velocity?

u = 0

What can be infered if an object is falling due to gravity in regards with SUVAT equations?

a = g = 9.81 ms^-2

Components of the stopping distance

• Thinking distance

• Braking distance

Thinking distance

Distance travelled by the vehicle from when the driver sees a problem and applies the brake

Formula of the thinking distance

Thinking distance = initial speed x reaction time

Proportional to the initial speed (u)

Time taken for the driver to respond to the problem

Factors affecting the thinking distance

• initial speed

• tiredness

• age

• distraction

• medication

• eyesight

• under the influence

Braking distance

The distance travelled by the vehicle after the driver has applied to the brake

Equation for braking distance

Time period when brakes are applied x average speed

Equation for work done by the brakes

Work done = braking force x braking distance x ½ mv²

Proportional to the square of the initial speed (u²)

All of the vehicles kinetic energy (½ mv²) must be dissipated by the brakes in order to stop

Factors affecting braking distance

• mass of the vehicle

• weather conditions

• initial speed

• car condition (e.g. tyres, brakes etc.)

The interaction with the thinking and braking distance and speed

Thinking distance increasing proportionally with speed:

• if the speed doubles, the thinking distance doubles

the braking distance increases at an even faster rate

Acceleration due to gravity

Objects with mass (mass-energy) exerts a force upon objects that have a force, known as gravitational force. The earth is very big so it forces objects to accelerate towards the centre of the Earth.

Free-fall

When an object is falling with no other forces acting on (ONLY IT’S OWN WEIGHT)

What is free fall denoted by?

g - 9.81 ms^-2

Variation in the value of g

Varies slightly around the Earth due to longitude, latitude and the local geology as it's not a perfect sphere

Projectile

An object thrown at an angle to the horizontal

Analysing projectile motion

• the horizontal and vertical components of the object’s motion are analysed independantly, but the time is interchangeable

• assume there is no air resistance

Time of flight of a projectile

How long the projectile is in the air

Maximum height of a projectile

The height at which the projectile is momentarily at rest

Range of a projectile

The horizontal distance travelled by the projectile

The horizontal acceleration of a projectile

Zero

The horizontal velocity of a projectile

Constant

The vertical acceleration of a projectile

9.81ms^-2 downwards

When is a projectile at the maximum height?

When the vertical v = 0

When does a projectile reach the ground?

When the vertical s = 0

What is the time taken to reach the maximum height (for a projectile?)

Half the total time in the air

The components of the horizontal vector (F_x)

F_x = F (cos (θ) )

in the x direction

The components of the vertical vector (F_y)

F_y = F (sin (θ) )

in the y direction

The angle made by the vector to the horizontal

tan θ = F_y / F_x