Confidence Intervals Unit 5

Confidence Interval Rule

The larger your confidence, the wider the interval (the more narrow the interval, the lower the confidence)

Statistical inference

Provides methods of drawing conclusions about a population from sample data; in formal inference, we use PROBABILITY to express the strength of our conclusions about a population from sample data

CL

Confidence Level

If the confidence procedure was repeated many times,

CL% of the resulting confidence intervals would contain the population mean

A level C confidence interval for a parameter has two parts:

1. An interval calculated from the data, usually out of the form estimate ± margin of error

2. A confidence level C, which gives the probability that the interval will capture the true parameter value in repeated samples

Constructing a confidence interval (the construction of a confidence interval for a population mean mu is appropriate when)

1. The data comes from an SRS from the population of interest

2. The sampling distribution of x-bar is approximately normal (if the population is normal or CLT for x-bar; rules of thumb for p-hat)

3. The sample is independent from the population (10n≤N)

Critical Values

The number z* (z star) with probability “p” lying to its right under the standard normal curve (called the upper p critical value of the standard normal deviation)

• First (1-C)/2 → Use Inversenorm

• C being the confidence level

• Critical values are ALWAYS positive

90% confidence level

.05 tail area & z*=1.6449

95% confidence level

.025 tail area & z*=1.96

99% confidence level

.005 tail area & z*=2.5758

Confidence Interval for a Population Mean

An SRS of size n from a population having an unknown mean mu and a known standard deviation sigma, has a level C confidence interval for mu

• this interval is exact when the population distribution is normal and approximately correct for large values of n

Conditions for a z interval

1. Must be an SRS

2. Must be approximately normal (CLT or population is approx normal)

3. Independence (10n≤N)

Steps to construct any confidence interval (PANIC)

P - Parameter of interest (The parameter of interest is ____)

A - Assumptions

N - Name the type of interval (__ sample, (z or t)__ interval, CL=___%, (if a t-dist, df=__)

I - Interval (calculate)

C - Conclusion in Context (I am ___% confident that the true mu of (parameter in context) lies between ___ and ____.

Behavior of confidence intervals

A small margin of error says that we have gotten really close to the parameter. We want high confidence and small margin of error which will make small intervals.

Margin of Error

Margin of error gets smaller when

z* get smaller and confidence level C gets smaller and sigma gets smaller and n gets larger

Since we use the square root of n, we must

take 4 times the same size to cut the margin of error in half

Since we use the square root of n, we must

take 4 times the same size to cut the margin of error in half

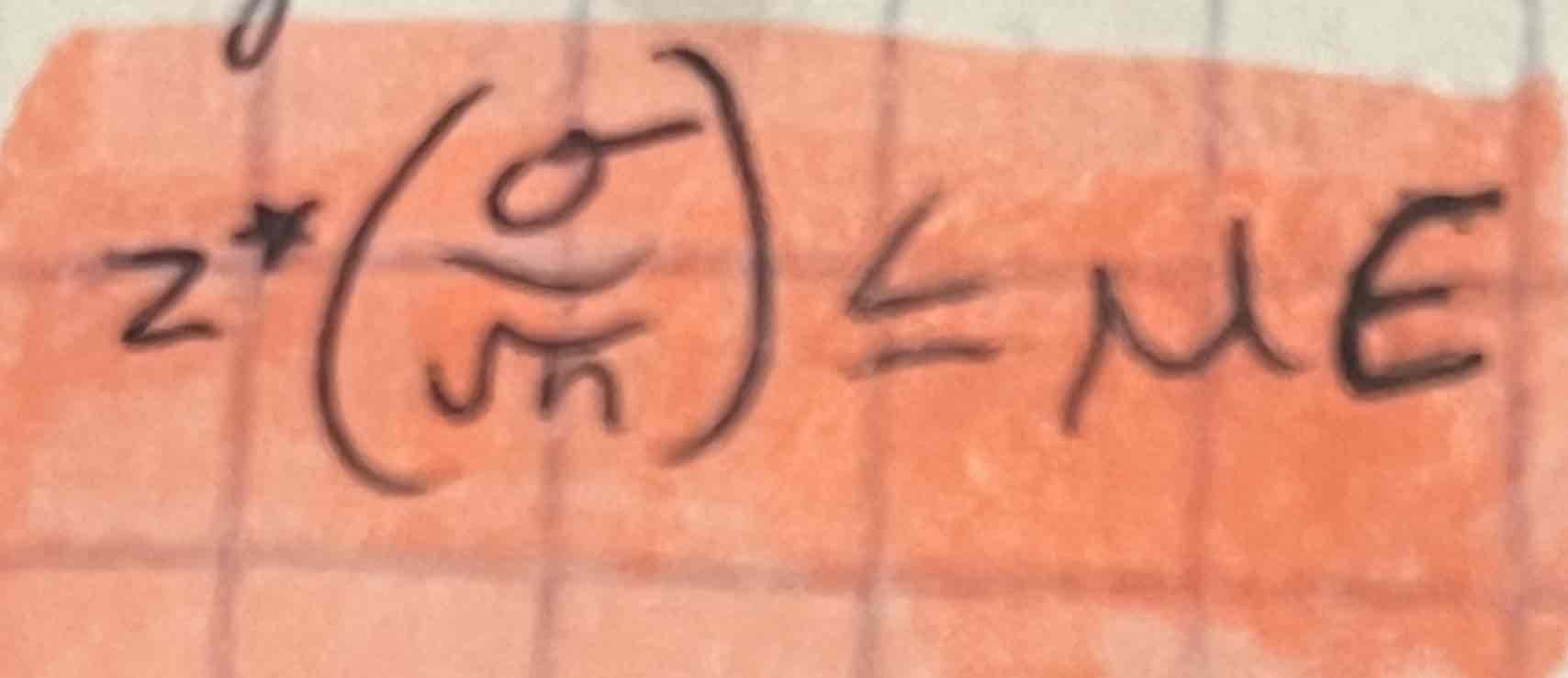
Sample size manufacturing

To determine the sample size n that will yield a confidence interval for population mean with specified margin of error, ME, set the expression for the margin of error to be less than or equal to mu and solve

• ALWAYS ROUND UP

NEVER use probability to

describe a confidence interval

T-distribution

• t is a standard value like z, t tells us how many standard deviations x-bar is from mu

• It is symmetric about a zero and is bell shaped, but there is more variation, so the spread is greater

• Must identify the degrees of freedom (n-1) because there is a different t statistic for each sample size

• Use t-table (gives are to the RIGHT of t)

• NO SIGMA; DOES NOT HAVE POPULATION STANDARD DEVIATION

As the df increases, the t-distribution

closer to normal since S is getting closer to signs

One sample t procedures are exactly correct only when

the population is normal (we assume it’s normal to justify it’s use)

One sample t procedures

To calculate one sample t-interval, we must still assume or know the following:

1. The data is from an SRS from the population of interest

2. The sample mean x-bar has a normal distribution (normal population, graphically supported (normal probability plot) or n≥30 for CLT)

3. Independent (10n≤N)

4. NAMING THE TEST: one sample t-interval, CL=__%, df=__.

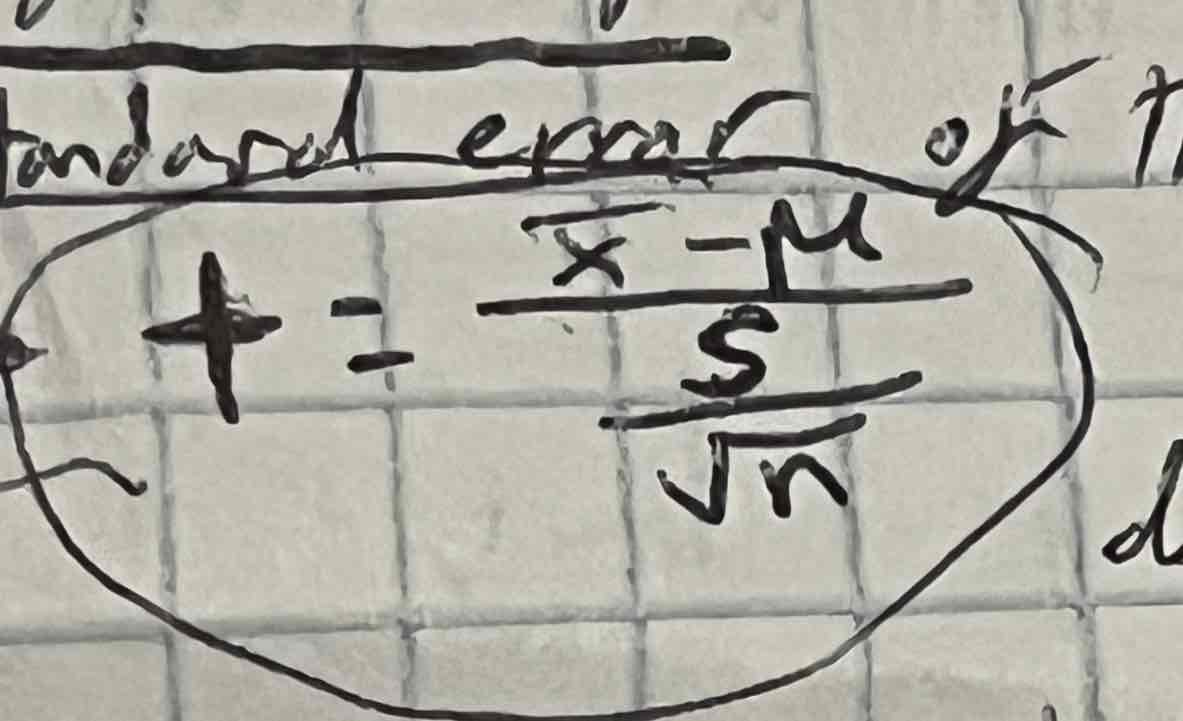
Z tests have

SIGMA, population SD