Paper 1 PMT flashcards

What is a force field?

A region in which a non-contact force is experienced by an corresponding interacting particle

What is an electric field?

A region in which a charged particle will experience a non-contact force.

What is electric field strength?

The force per unit charge experienced by a charged particle when placed at that point in the field

State the equation used to calculate the force a charge experiences in an electric field.

Force = Electric Field Strength x Charge

F = EQ

What law determines the magnitude of the electric force between two charges?

Coulomb's Law

State Coulomb's law in words.

The force between two charges is directly proportional to the product of their charges and inversely proportional to the square of their separation

Give Coulomb's law in equation form

F = kQq/r²

where k = 1/4πε₀

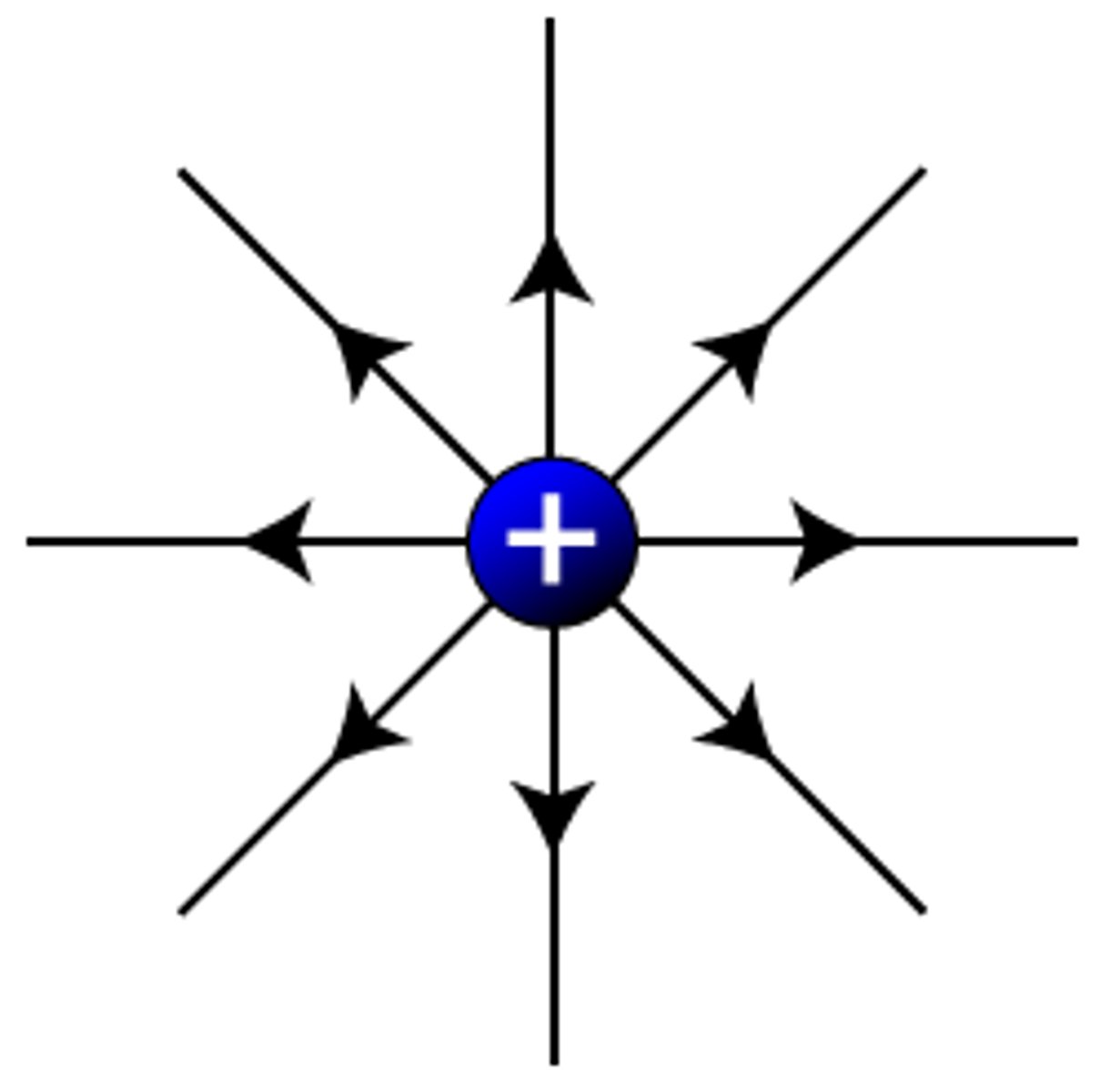
Describe the electric field pattern around a positive point charge.

A radial field, acting outwards.

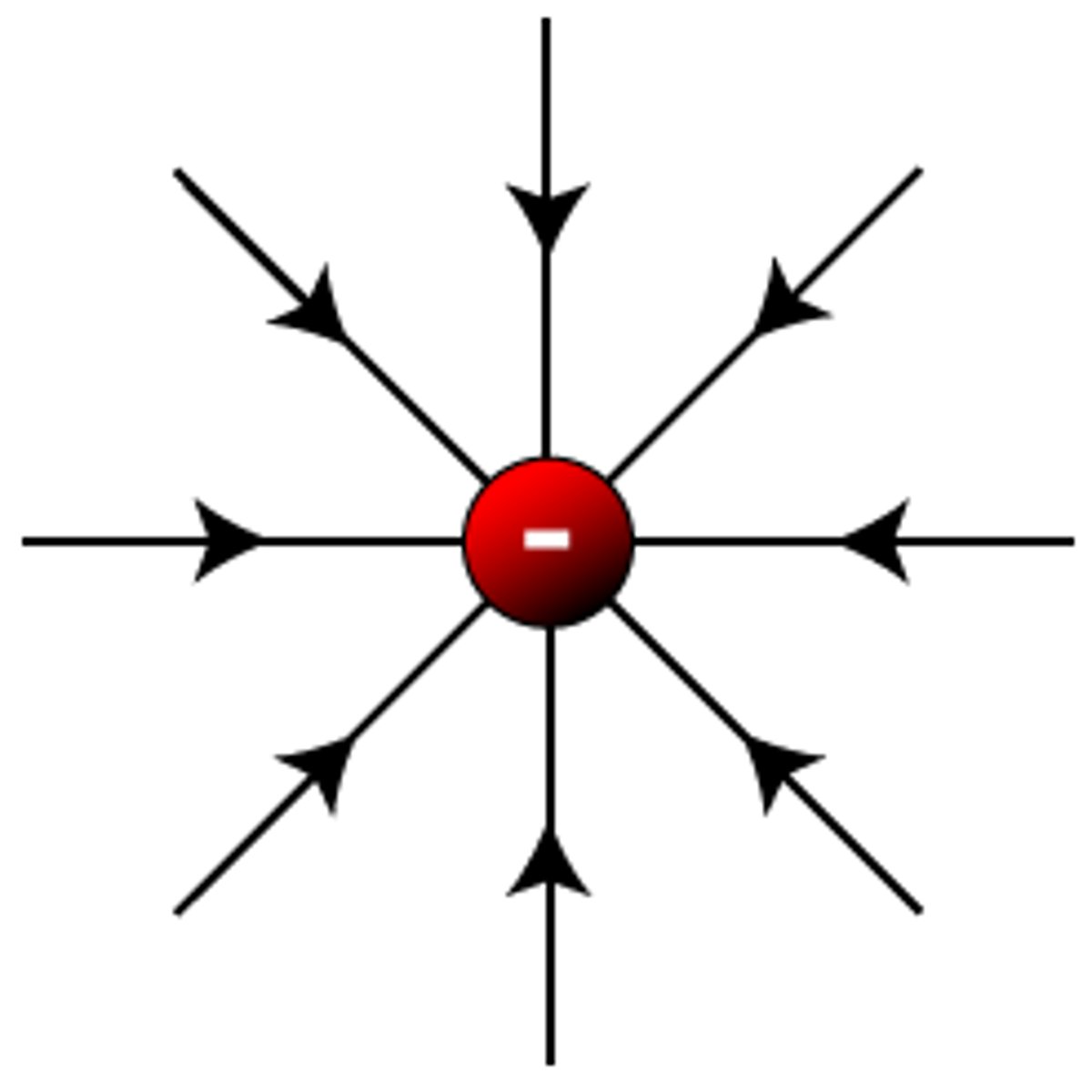
Describe the electric field pattern around a negative point charge.

A radial field, acting inwards.

Describe the uniform electric field between parallel plates.

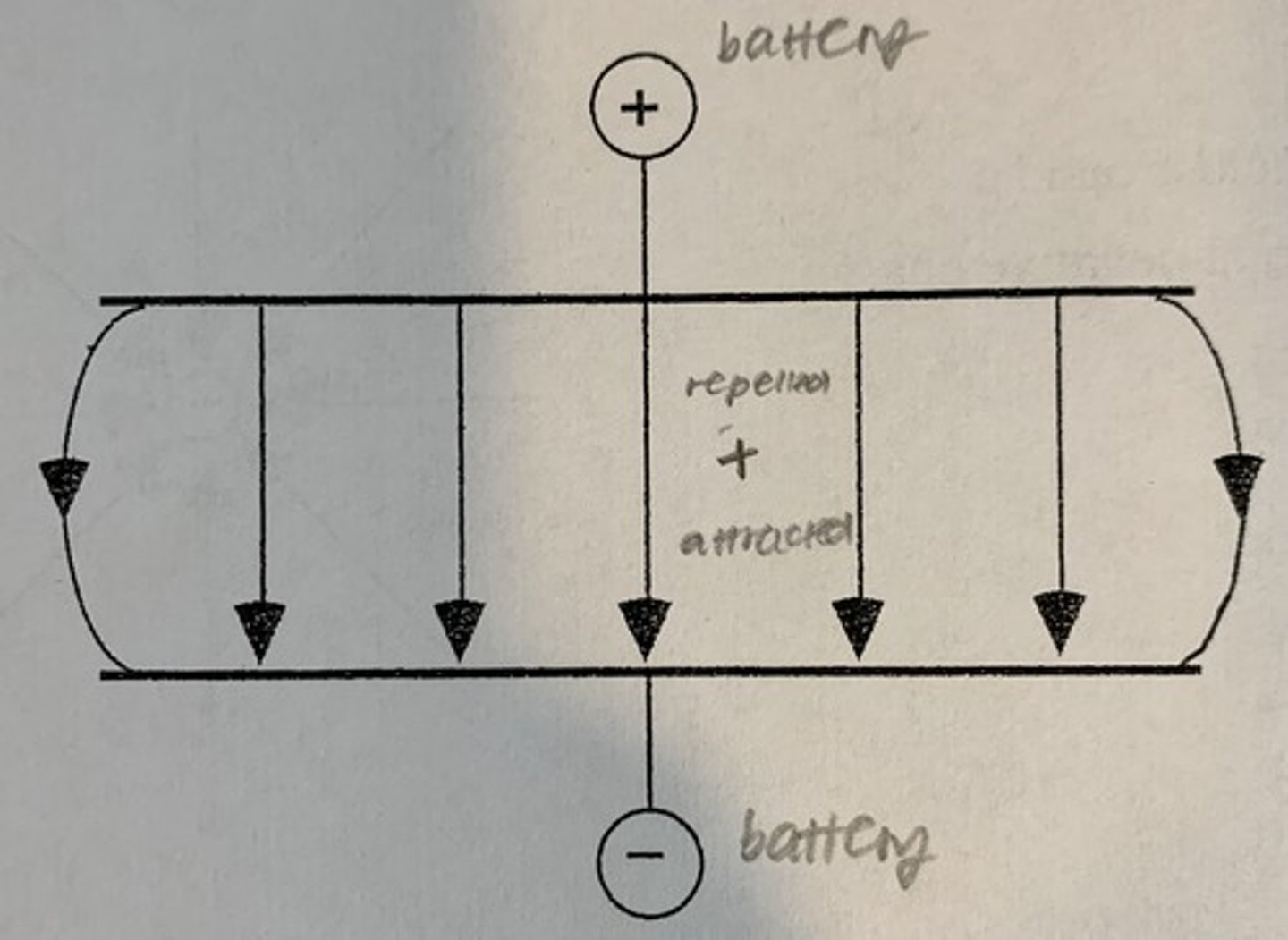
What equation is used to calculate the electric field between parallel plates?

E = V/d

What is electric potential?

The amount of energy required to move a positive test charge from infinity to a given point in an electric field.

How do you calculate electric potential for a radial field?

F = kQ/r

where k = 1/4πε₀

What are equipotentials?

Equipotentials are lines along which the electric potential remains the same

How do you calculate the work done in moving a charge along an equipotential?

No work is done when moving a charge along an equipotential since the electric potential doesn't change

What does a capacitor do?

Capacitors are used to store charge in a circuit.

What two factors determine how much charge can be stored by a capacitor?

1. The potential difference across it

2. The capacitance

What is capacitance?

Capacitance is a measure of how much charge can be store by a capacitor per unit potential difference across it.

State the equation used to calculate the capacitance from the charge and potential difference.

Capacitance = Charge / Potential Difference

C = Q/V

What is the unit of capacitance?

CV⁻¹

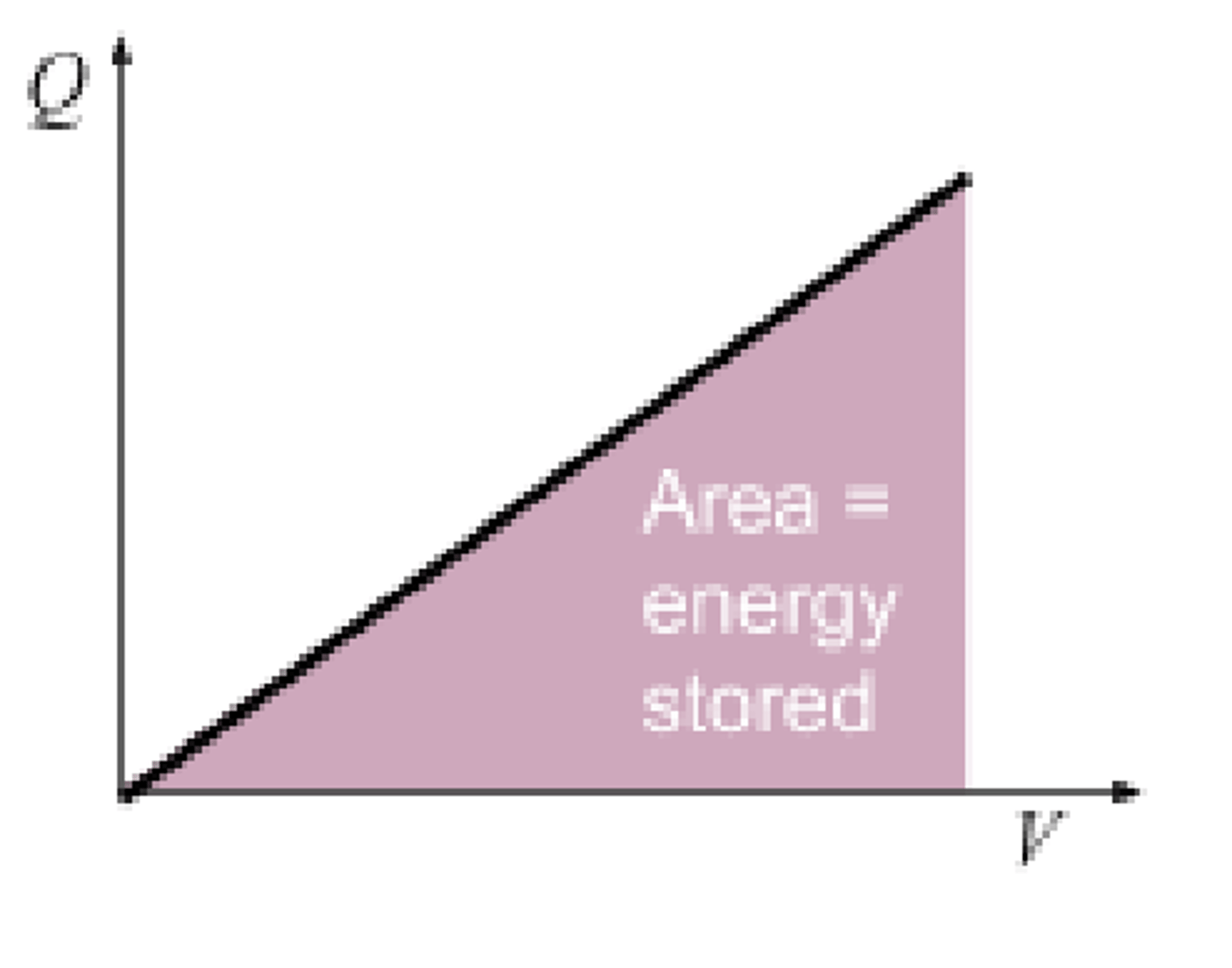
What is represented by the area under a capacitor's charge-potential graph?

The energy stored by a capacitor

What is represented by the gradient of a capacitor's charge-potential graph?

Capacitance

Give three equations to calculate the energy stored by a capacitor.

- W = ½ QV

- W = ½ CV²

- W = ½ Q²/C

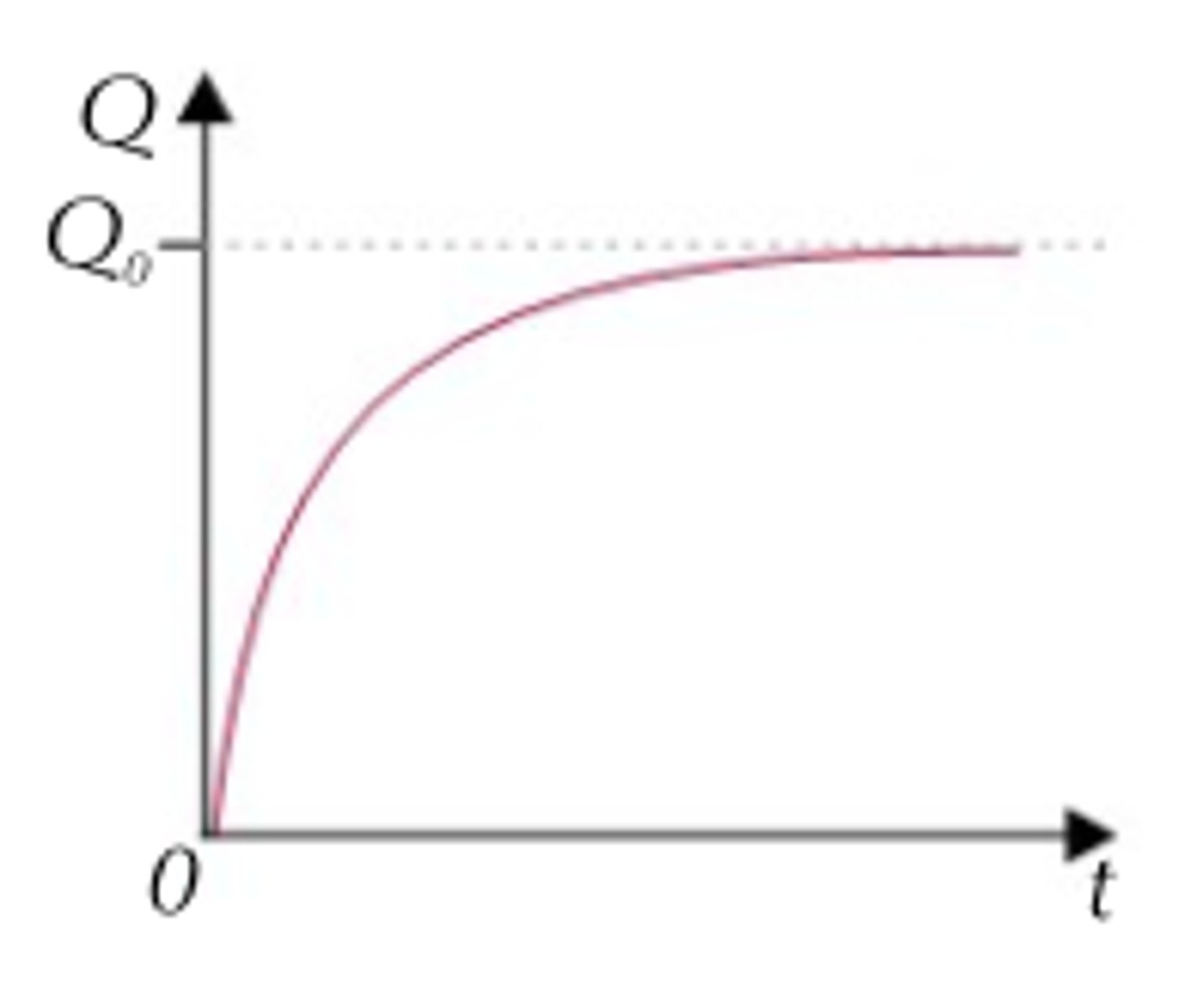
Describe a charge-time graph for charging a capacitor. What does the gradient represent?

Gradient = current

Describe a current-time graph for charging a capacitor. What does the area represent

Area = charge

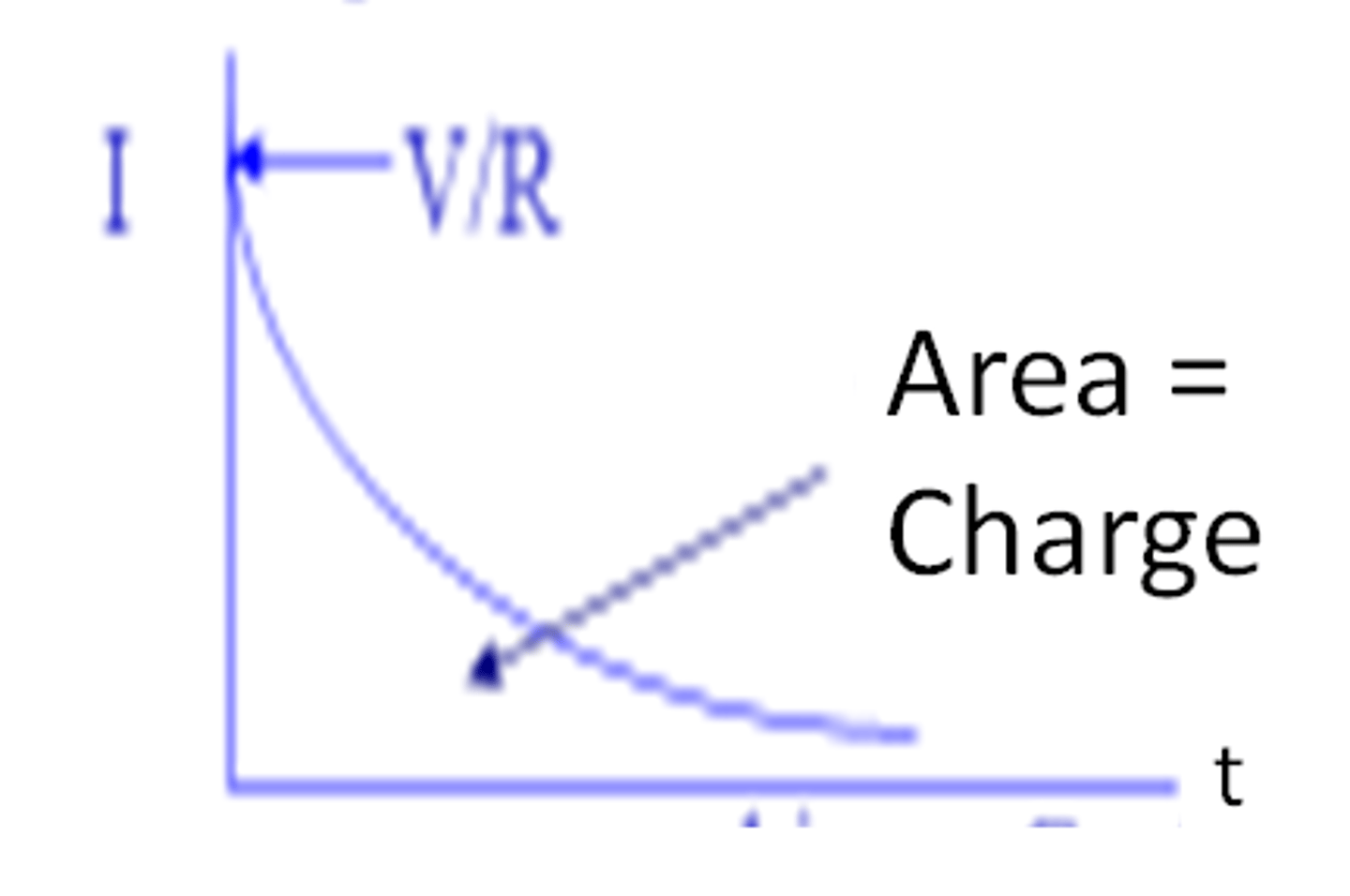
Describe a voltage-time graph for charging a capacitor.

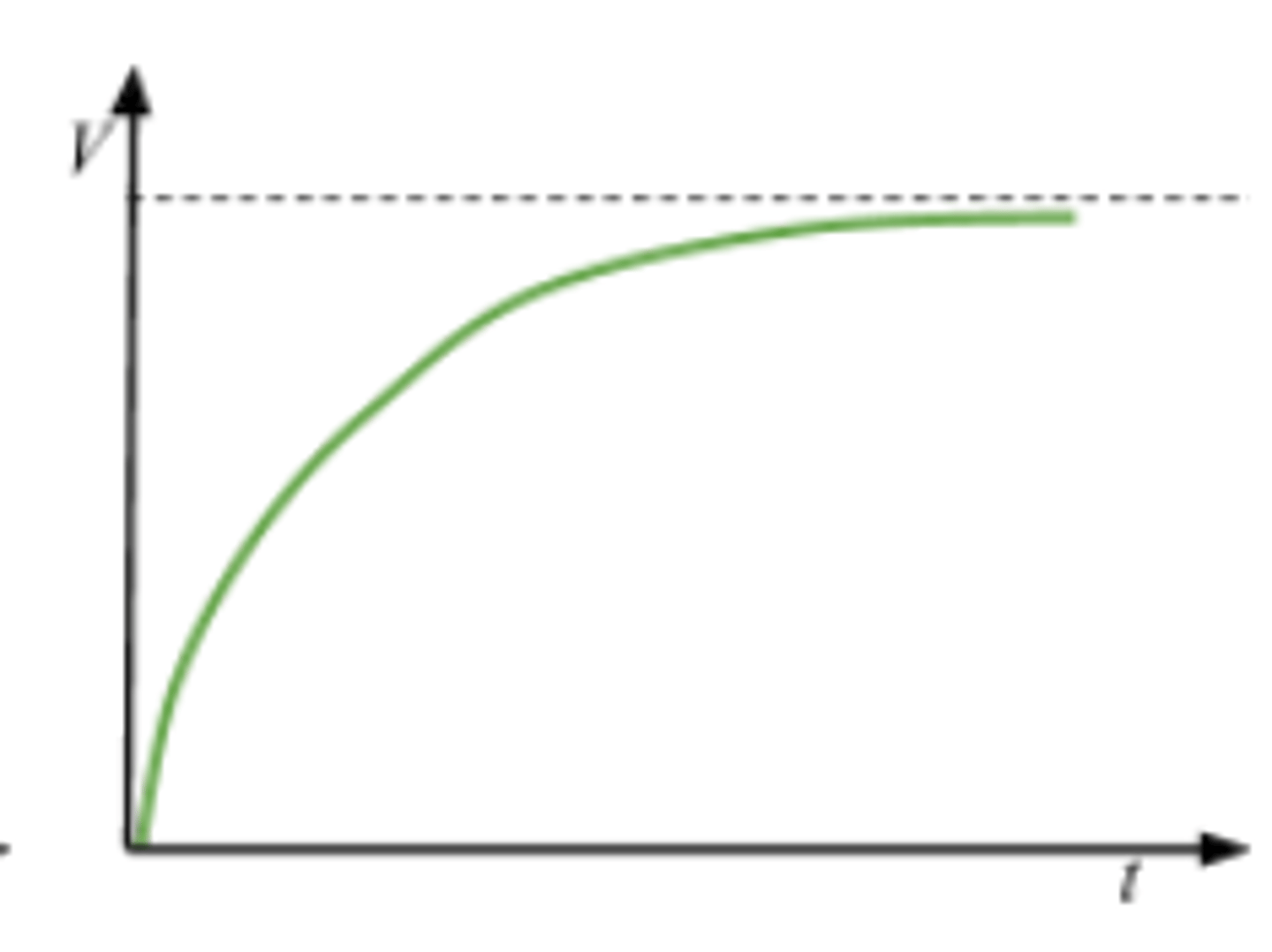
What value is given by the product of resistance and capacitance?

The time constant of the circuit.

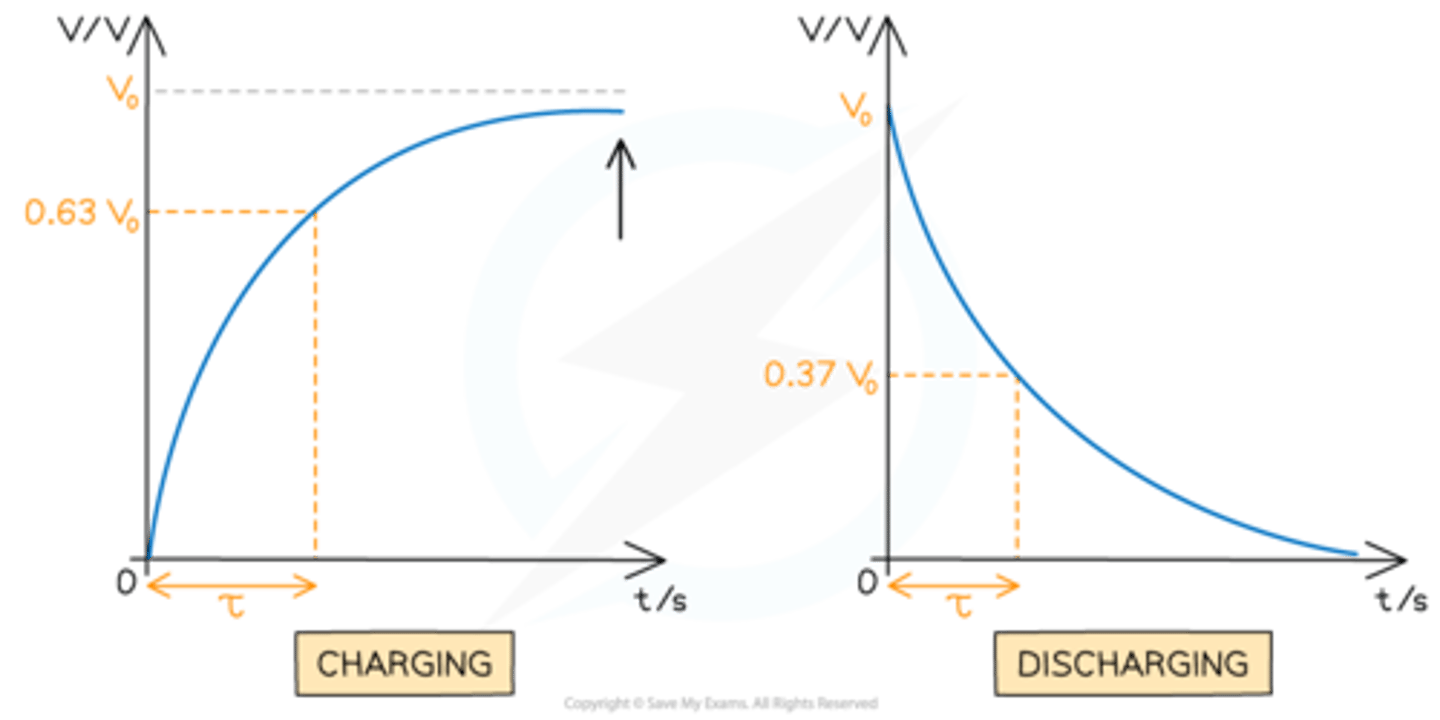
What does the time constant of a circuit tell you?

The time the capacitor will take to reach 63% of its total charge, and the time taken for it to discharge to 37% of its full charge.

What is a magnetic field?

A magnetic field is a region in which a magnetic pole will experience a non-contact force.

In which direction do magnetic field lines point?

From North to South

What is magnetic flux density?

Magnetic flux density is a measure of the strength of a magnetic field. It can be viewed as the number of magnetic field lines that pass through a given area.

What three factors determine the force exerted on a charge moving through a magnetic field?

1. The magnetic flux density

2. The charge of the particle

3. The velocity of the particle perpendicular to the field

State the equation used to calculate the force exerted on a charge moving through a magnetic field.

F = Bqvsinθ

What is the relationship between the direction of a charge's motion and the direction of the magnetic force it experiences?

The force is always perpendicular to the charge's motion.

Describe and explain the path taken by a charge in a magnetic field.

The charge will move in a circular path. This is because the magnetic force always act perpendicular to the charge's motion and so acts as a centripetal force.

What is produced by a current-carrying wire?

A magnetic field is produced in concentric circles around a wire when a current passes through it.

What occurs when a current-carrying wire is placed in a magnetic field?

The wire will experience a force due to the permanent magnetic field interacting with the wire's magnetic field.

What three factors affect the forces experienced by a current-carrying wire placed in a magnetic field?

1. The magnetic flux density of the field

2. The current passing through the wire

3. The length of the wire

State the equation used to calculate the force experienced by a current-carrying wire placed in a magnetic field.

F = BILsinθ

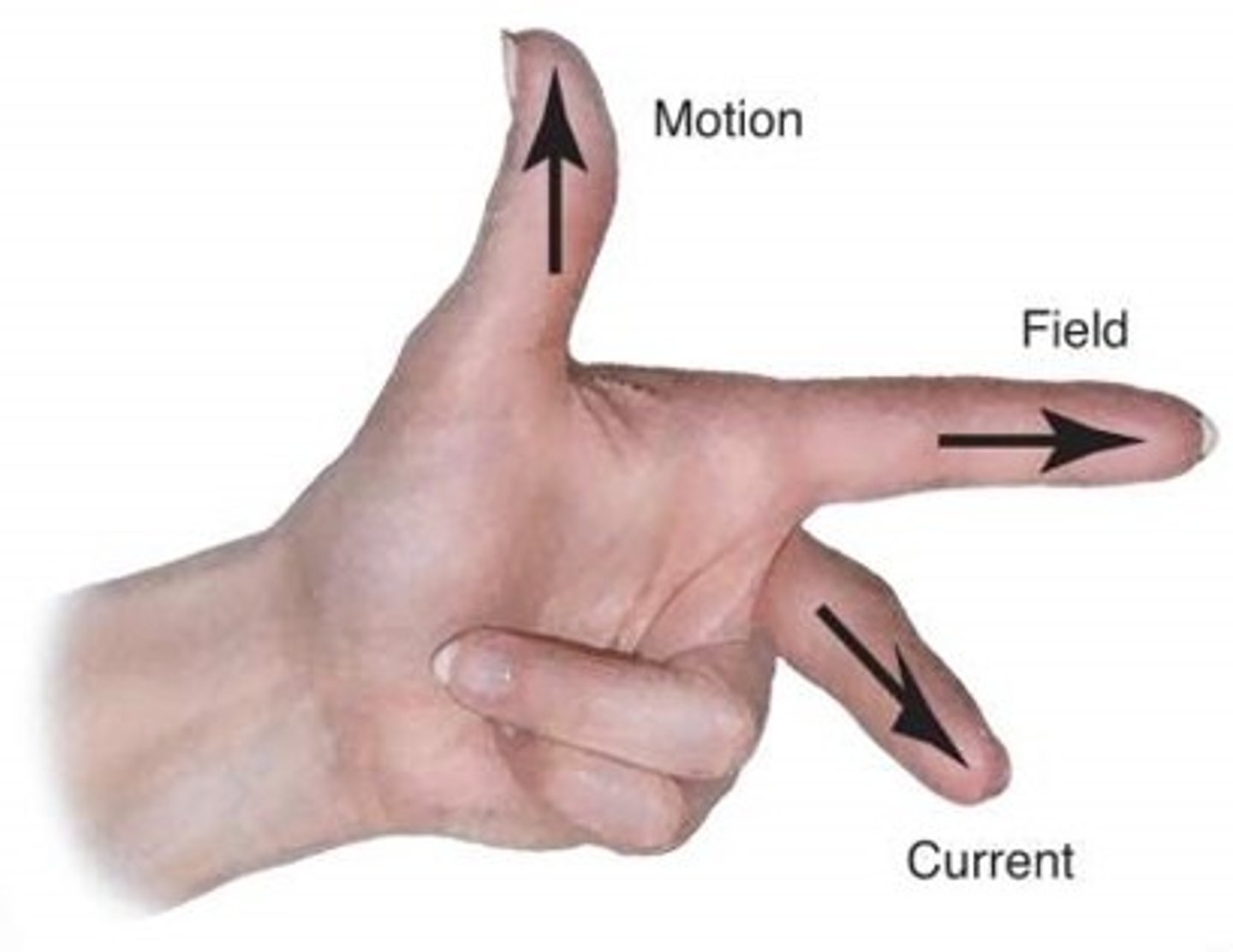
What is Fleming's left-hand rule used for?

To determine the direction of the force experienced by a current-carrying wire or moving charge in a magnetic field.

What does the thumb represent in Fleming's left hand rule?

The thumb represents the direction of the force.

What does the first finger represent when using Fleming's left-hand rule?

The direction of the field.

What does the second finger represent when using Fleming's left-hand rule for a moving charge?

The direction that a positive charge would move. This means that if it is a negative charge, you must point your second finger on the opposite direction to its motion

What does the second finger represent when using Fleming's left-hand rule for a current-carrying wire?

The direction of conventional current flow.

All charged particles and surfaces produce an electric field around themselves. An electric field is a region where charged particles experience a non-contact force. Unlike gravitational fields, this force can be attractive or repulsive.

- Same charges repel each other

- Opposite charges attract each other

Electric field lines point in the direction that a positive charge would experience a force and so point from positive to negative

The force that acts between two charges is determined by Coulomb's Law. This states that:

- The force is directly proportional to product of the charges involved

- The force is inversely proportional to the square of the separation between the two charges.

As an equation, this is:

F = KQq/r²

where K = 1/4πε₀

If the force has a positive value, it is a repulsive force.

If the force has a negative value, it is an attractive force.

Electric field strength (E) is defined as the electrostatic force that a unit positive charge would experience, at a given point in the field. As an equation, this is:

E = F/Q

There are two further equations for finding the electric field strength, this first is for a radial field, while the second is for a field formed by parallel plates:

- E = KQ/r²

where K = 1/4πε₀

- E = V/d

The electric field strength around a point charge decreases as you move further away from it.

The weaker the electric field strength, the less dense the electric field lines are.

Electric Potential at a point is the amount of work done in moving a unit positive point charge from infinity to that point. As an equation this is:

- V = KQ/r

where K = 1/4πε₀

Electric potential difference is the work done moving a positive charge from one point to another.

This means that when you move a charge through a potential difference, work is done, equal to: ΔW = QΔV

As with gravitational fields, equipotentials are planes of points where the electric potential is the same, consequently no work is done when moving along these lines.

The capacitance (C) of a capacitor is the amount if charge it can store per unit of potential difference, measured in Farads.

C = Q/V

Capacitors consist of two metal plates separated by a dielectric. The capacitance of a given capacitor depends on the surface area of the plates, their separation and the dielectric being used.

C = Aε₀εr/d

A number of equations can be used to calculate the energy stored in a capacitor. The second and third equations are derived by substituting the capacitance equation into the first.

- E = ½QV

- E = ½CV²

- E = Q²/C

The energy stored can also be calculated by determined the area under a charge-voltage graph. The first energy stored equation above is derived from this fact.

The gradient of the graph is equal to the capacitance

You should know the shapes of the charging and discharging graphs for a capacitor, for potential difference, charge and current.

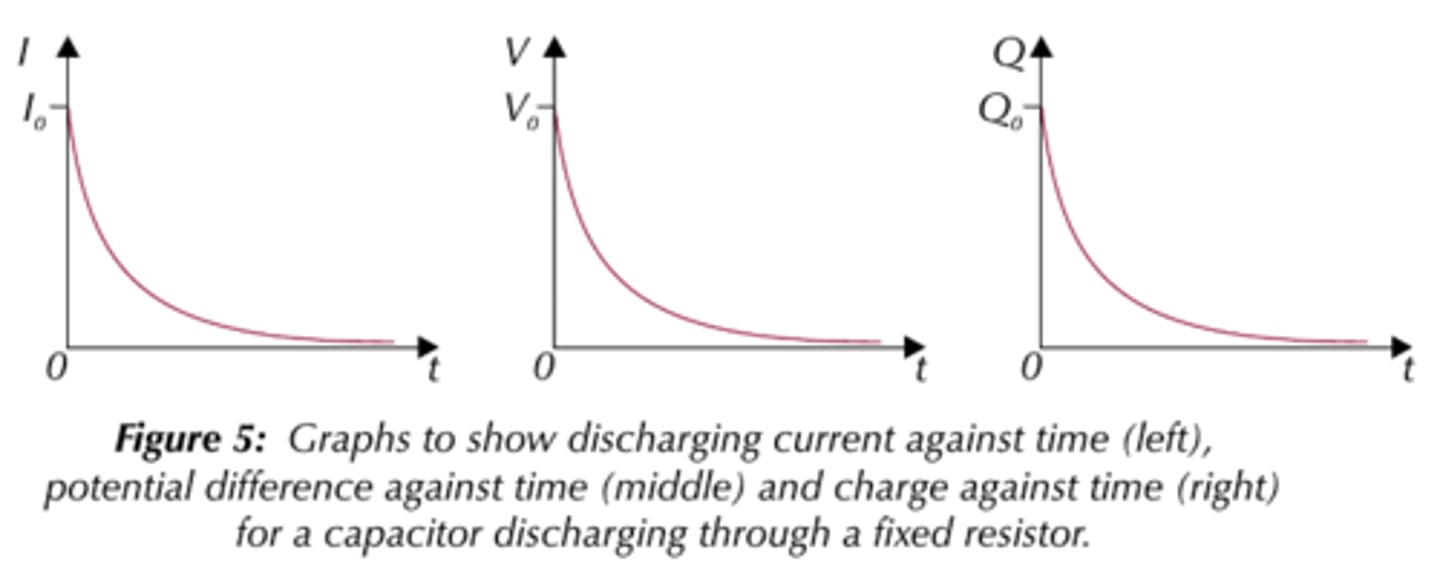
You should know the following formulas for the current, potential difference and charge of a discharging capacitor:

- I = I₀e⁻ᵗ/ᴿᶜ

- V = V₀e⁻ᵗ/ᴿᶜ

- Q = Q₀e⁻ᵗ/ᴿᶜ

You should also be able to derive the following equations by taking natural logarithms of both sides of the equations, and simplifying them using the log rules:

- ln I = lnI₀ - t/RC

- ln V = lnV₀ - t/RC

- ln Q = lnQ₀ - t/RC

An important value when working with capacitors is the time constant. It is equal to:

- The product of the resistance in the circuit and the capacitance of the capacitor

- The time taken to charge the capacitor to (1 - 1/e) of its final value.

- The time taken to discharge the capacitor to 1/e of its initial value.

When current passes through a wire, a magnetic field is induced around it. This field consists of concentric circles around the wire.

Magnetic flux density is a measure of the strength of a field and its unit is the Tesla

If a current carrying wire is placed in a magnetic field, the two fields interact and a force acts on the wire. The magnitude of this force depends on:

- The length of the wire

- The current passing through the wire

- The magnetic flux density of the field

When a current-carrying wire experiences a force in a field, it is referred to as the motor effect. The magnitude of the force can be calculated using:

Force (N) = Magnetic Flux Density (T) x Current (A) x Length of Wire (m)

- F = BIL sinθ

The direction of the force (motion) can be determined using Fleming's Left Hand rule

When a charge moves in a magnetic field, it will experience a force. The magnitude of this force depends on:

- The magnitude of the charge

- The magnetic flux density of the field

- The velocity of the charge

The equation used to calculate the force is:

Force (N) = Magnetic Flux Density (T) x Charge (C) x Velocity (ms⁻¹)

F = BQv sinθ

Use Fleming's Left Hand Rule to determine the direction, with the second finger being the direction of a positive charge (so if its a negative charge, point it in the opposite direction)

Magnetic flux is a measure of the magnetic field that passes through a given area. It can be thought of as a measure of the number of field lines passing through the surface, or the density of the field line that are passing through it.

Magnetic Flux (Wb) = Magnetic Flux Density (T) x Area(m²)

ϕ = BA

This only applies when the magnetic field lines are perpendicular to the area.

If using a coil, a more useful quantity is magnetic flux linkage. This is the magnetic flux multiplied by the number of turns of the coil the field passes through.

Nϕ = B A N

If a current-carrying conductor moves relative to a magnetic field , an EMF is induced. This is as a result of the charge carriers in the conductor experiencing a force. If the conductor forms a complete loop, a current flows as a result of the induced EMF.

The law that governs the magnitude of the induced EMF is Faraday's Law which states that:

The magnitude of the induced EMF is directly proportional to the rate of change of magnetic flux linkage.

As an equation, this is:

- ε = N Δϕ/Δt

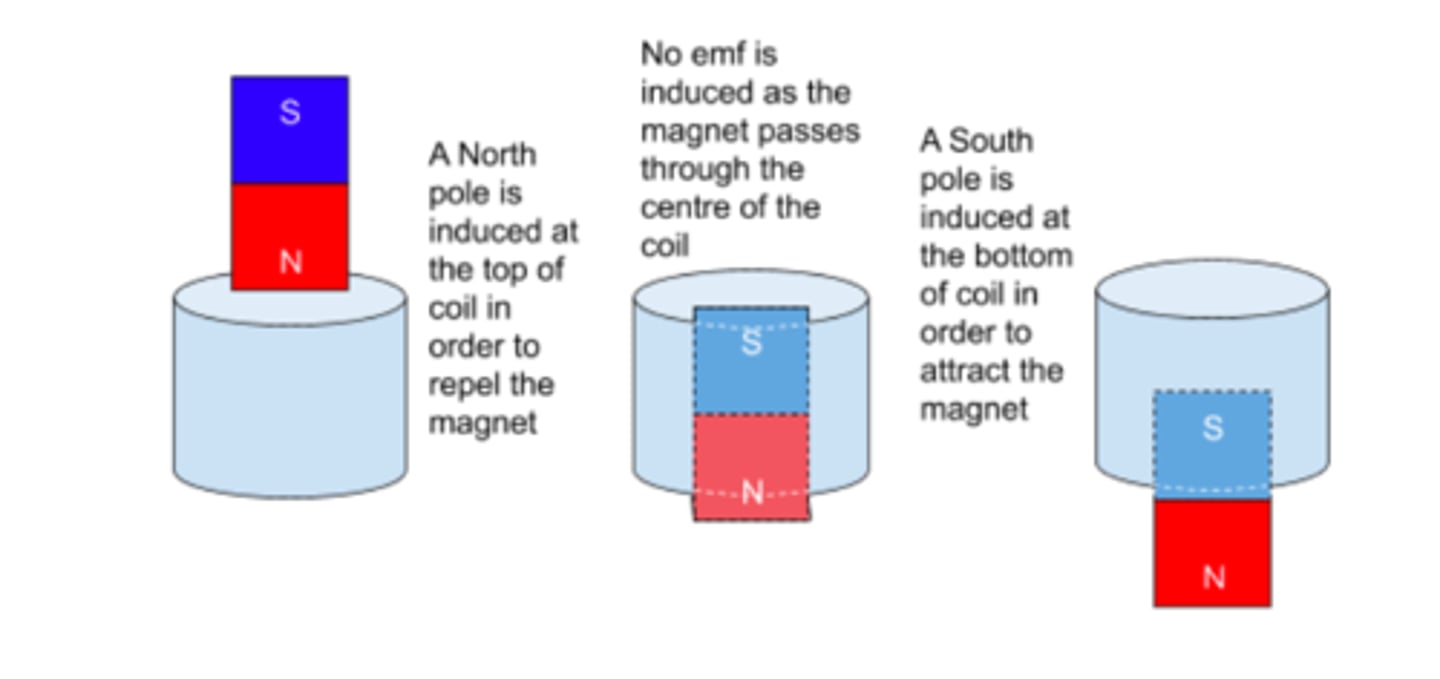
The direction of the induced EMF is governed by a second law known as Lenz's Law. This states that:

The direction of an induced current is such that is opposes the change that created it.

An example of this is a magnet falling through a non-magnetic metal tube.

Faraday's and Lenz's laws can be combined in order to form the following equation for the value of emf generated:

ε = -d(Nϕ)/dt

This equation shows the magnitude of induced emf is equal to the rate of change of flux linkage, and that the emf is induced in the opposite direction to the change causing.

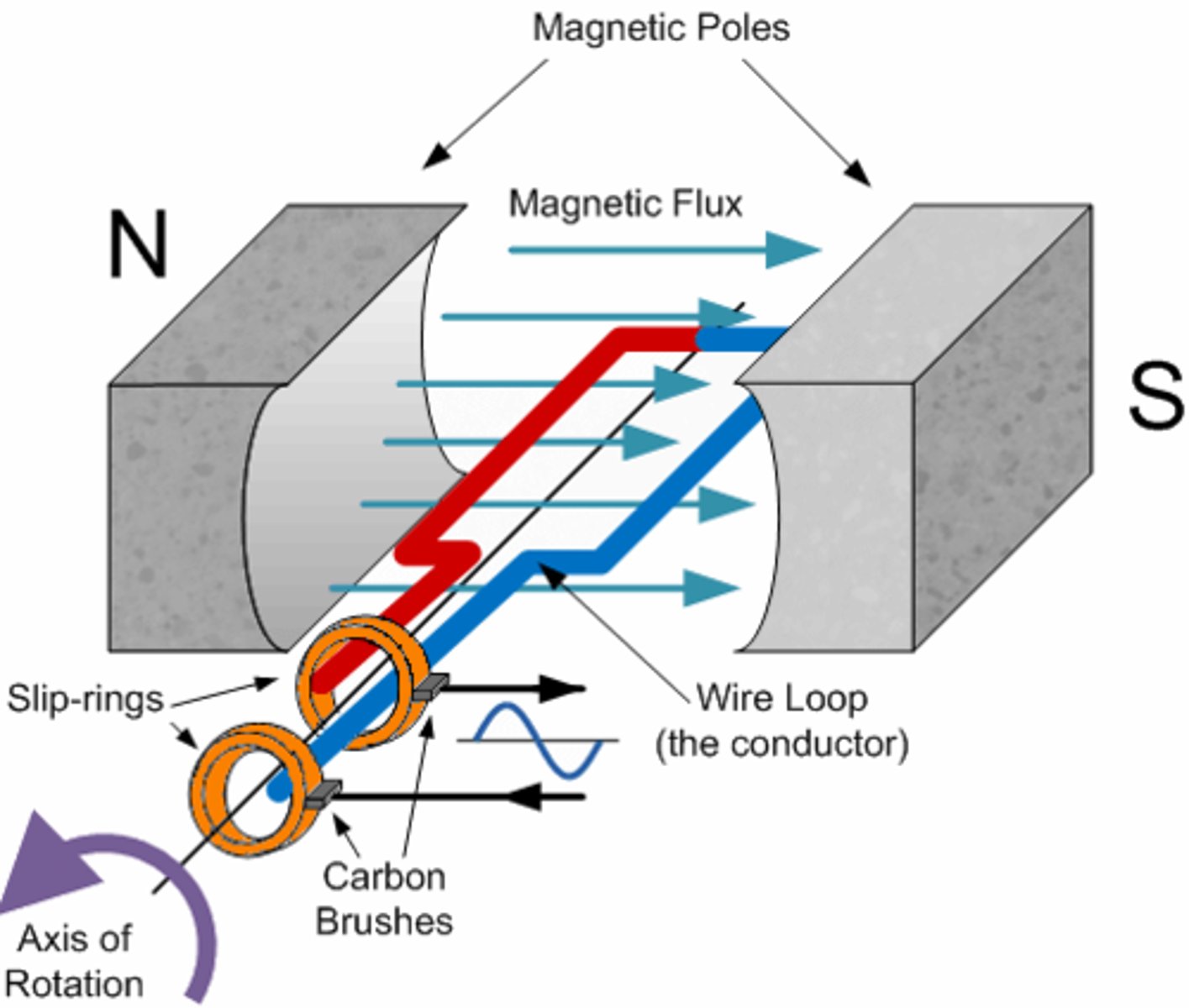
An A.C generator consists of a metal coil in a magnetic field. As the coil turns, the changing magnetic flux linkage passing through it induces an EMF.

The flux linkage varies sinusoidally between +BAN and -BAN.

- Nϕ = -BANcosωt

According to Faraday's law, the EMF is the rate of change of flux linkage.

- ε = ωBANsintωt

Increasing the speed/frequency of rotation or increasing the magnetic flux density will increase the maximum EMF.

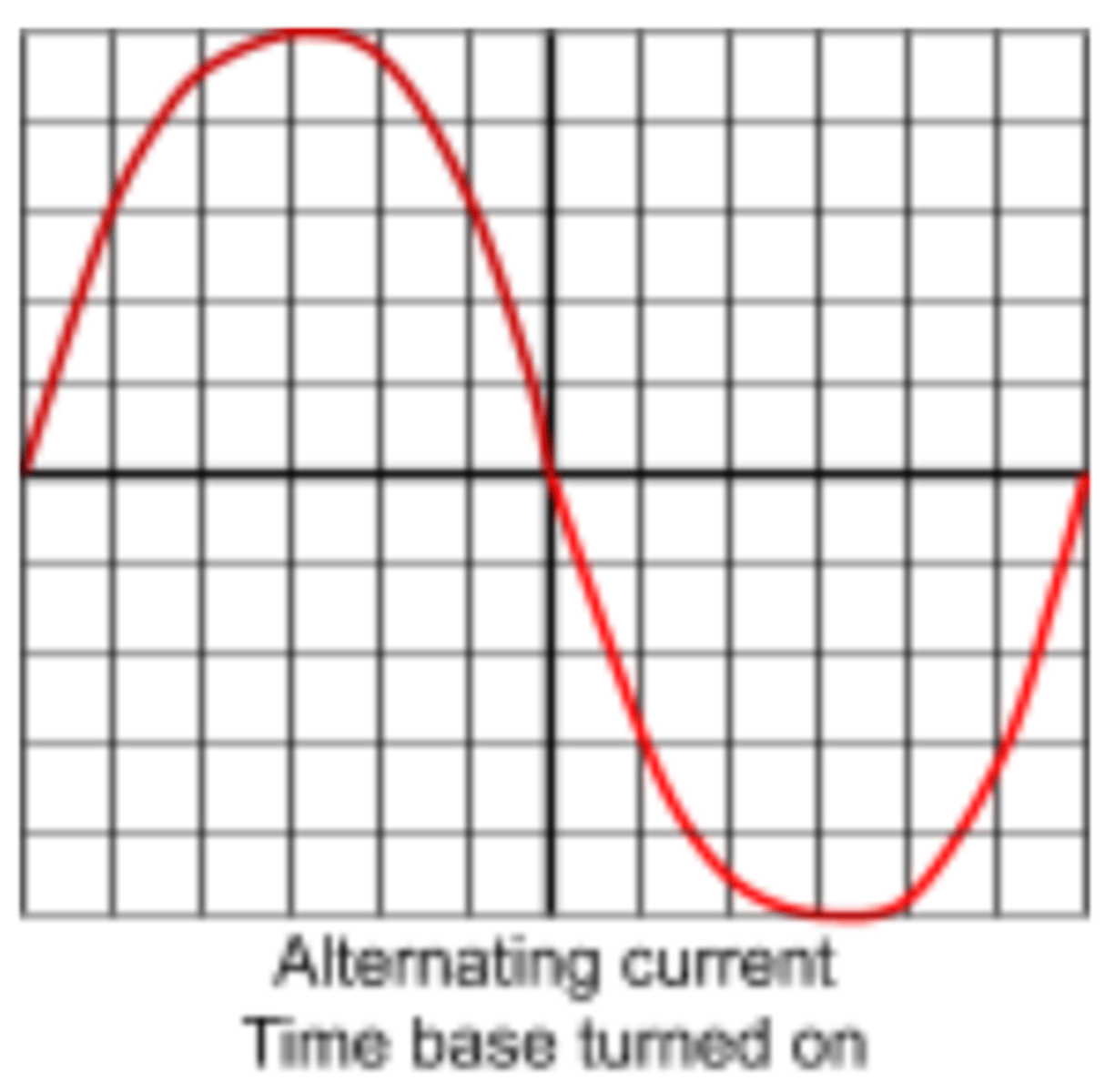
An oscilloscope is used to show voltage against time.

The time base controls how fast the wave moves across the screen (e.g. 2ms per division)

the Y-gain is the voltage per division (e.g. 2V per division.)

Vᵣ = V₀/√2

Iᵣ = I₀/√2

V₀ is the peak voltage. However the 'average voltage' is not the peak voltage, and therefore we find the root mean square (rms).

The rms value is usually quoted when referring to a AC power supply.

Powerᵣ = Iᵣ x Vᵣ

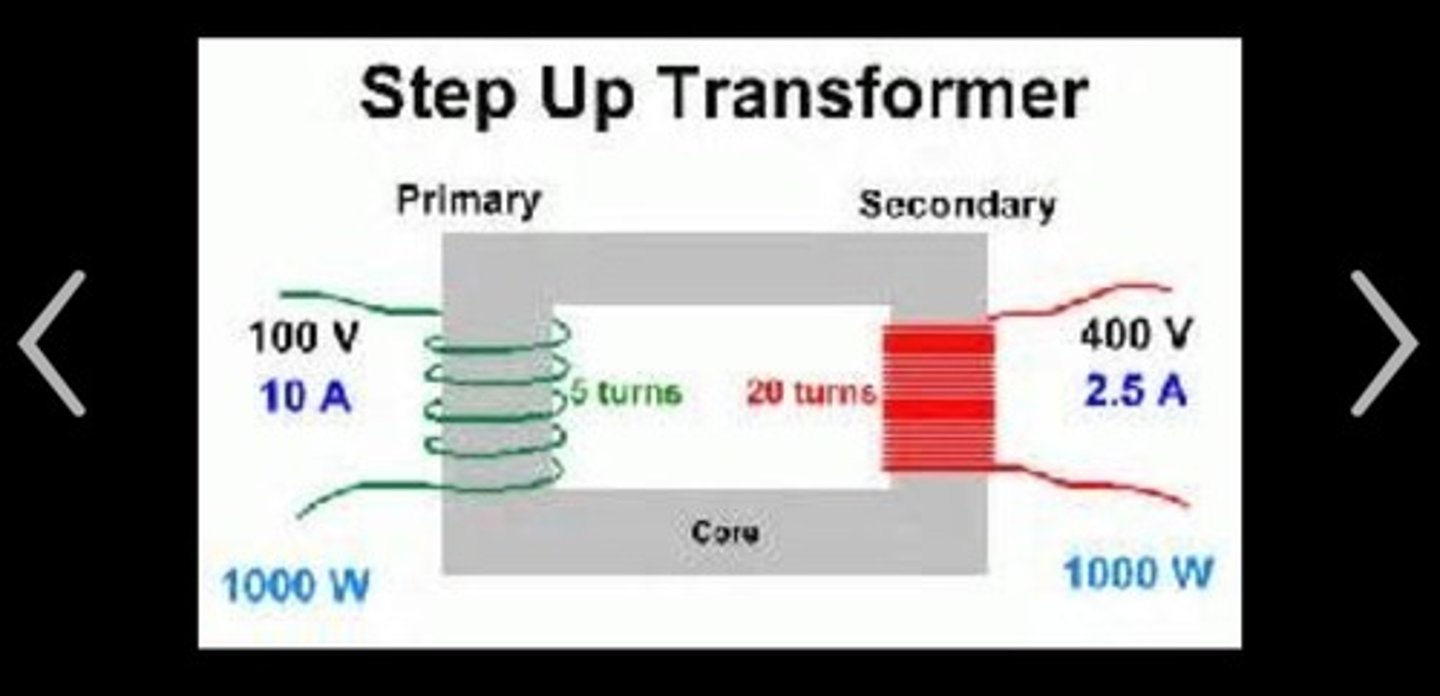
Transformers are used to increase or decrease the voltage of a power source. They come in two main types:

1. Step-Up: Number of coils on secondary coil > Number of coils on primary coil

2. Step-Down: Number of coils on primary coil > Number of coils on secondary coil

- A current passes through the primary coil which induces a magnetic field in the core.

- The current is an alternating-current so that the magnetic field in the core is constantly changng

- This constantly changing field causes a change of flux linkage in the secondary coil, which induces an EMF and therefore a current.

Inefficiencies:

If a transformer was 100% efficient, the power input would equal the power output - however power is lost due to:

- Eddy currents (looping currents which generate heat in the core)

- Heat loss in the wires

- Work done when magnetizing and demagnetizing the core

To reduce these factors:

- The core can be laminated to prevent eddy currents flowing

- The wires can be low resistance wires to reduce heating

- The core can be made from soft iron which is easily magnetized.

Define electrical current

Electrical current is the rate of flow of charge

State the defining equation for current.

I = ΔQ/Δt

What is the unit of current?

Ampere (Amps), A

Define voltage

Voltage is the work done per unit charge.

State the defining equation for voltage

V = W/Q

What equation links current, voltage and resistance?

Voltage (V) = Current (A) x Resistance (Ω)

V = IR

What is Ohm's Law?

If Ohm's law is obeyed, the current and voltage passing through a component are directly proportional, when at a constant temperature.

Describe the distribution of current in a series circuit.

In a series circuit, the current is the same at all positions in the circuit.

What law is the distribution of current in a series circuit a consequence of?

The law of the consequence of charge. Charge cannot be created or destroyed and so in a closed loop, the flow of charge must be the same throughout.

Describe the distribution of current in a parallel circuit.

In a parallel circuit, the current is split between the different branches. The current entering each branch must be the same as the current leaving it.

Explain how the conservation of charge applies to parallel circuits.

Charge cannot be created or destroyed meaning the total current leaving the source must equal the sum of the currents in all the individual branches

What law is the distribution of potential differences in a circuit a consequence of?

The law of the conservation of energy.

Describe the distribution of potential differences in a series circuit.

The total potential difference is split across all the components in a series circuit, in the ratio of their resistances.

Describe the distribution of potential differences in a parallel circuit.

The sum of the potential differences in each branch of a parallel circuit, is the same and will be equal to the potential difference of the source.

What equation relates power, current and potential difference?

P = IV

How can you calculate the work done over a given time period, by a component with a known potential difference and current?

Combining P = W/t and P = IV gives :

W = IVt

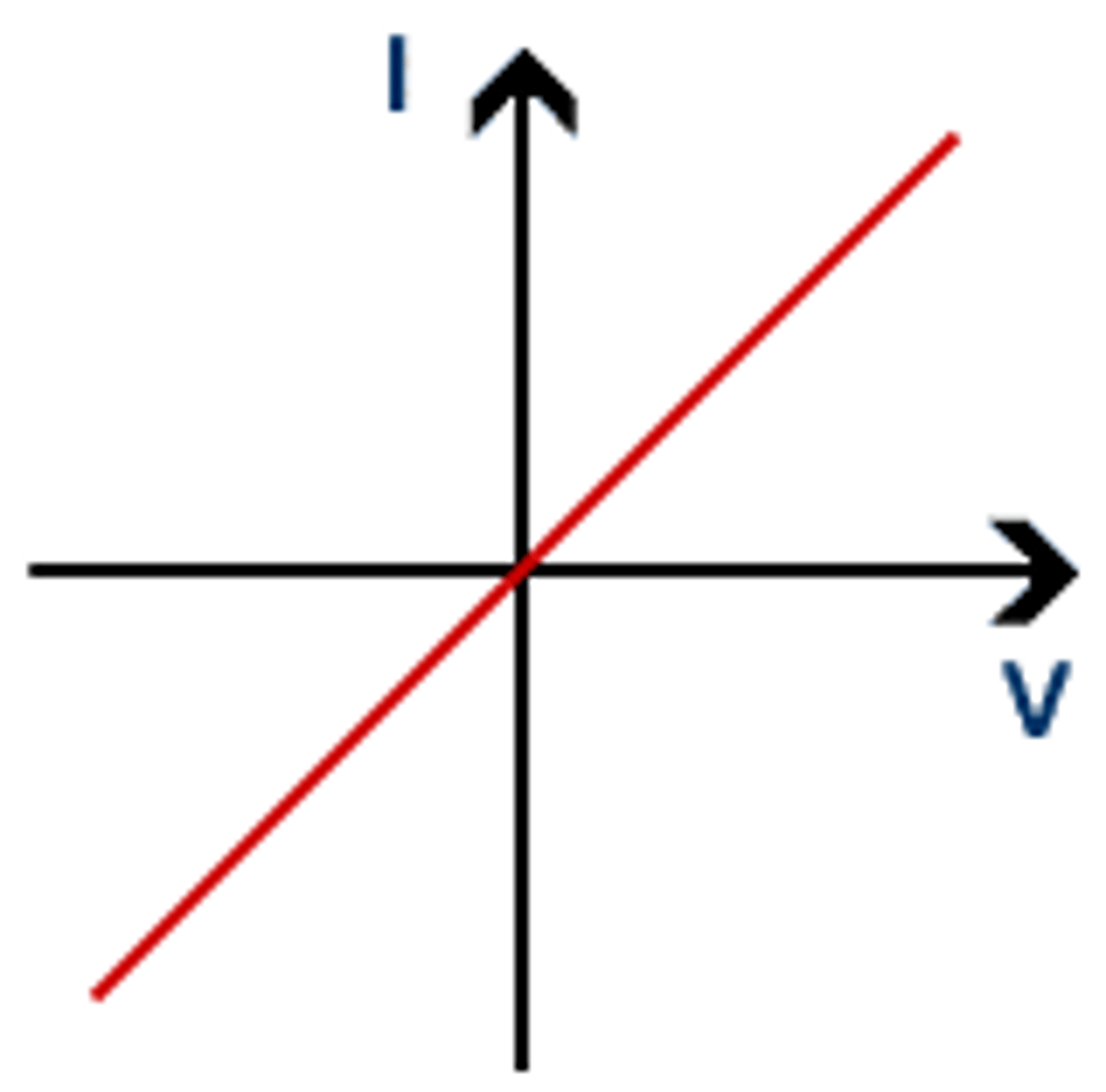
What is the IV characteristic for an ohmic conductor?

What is the IV characteristic for a filament bulb?

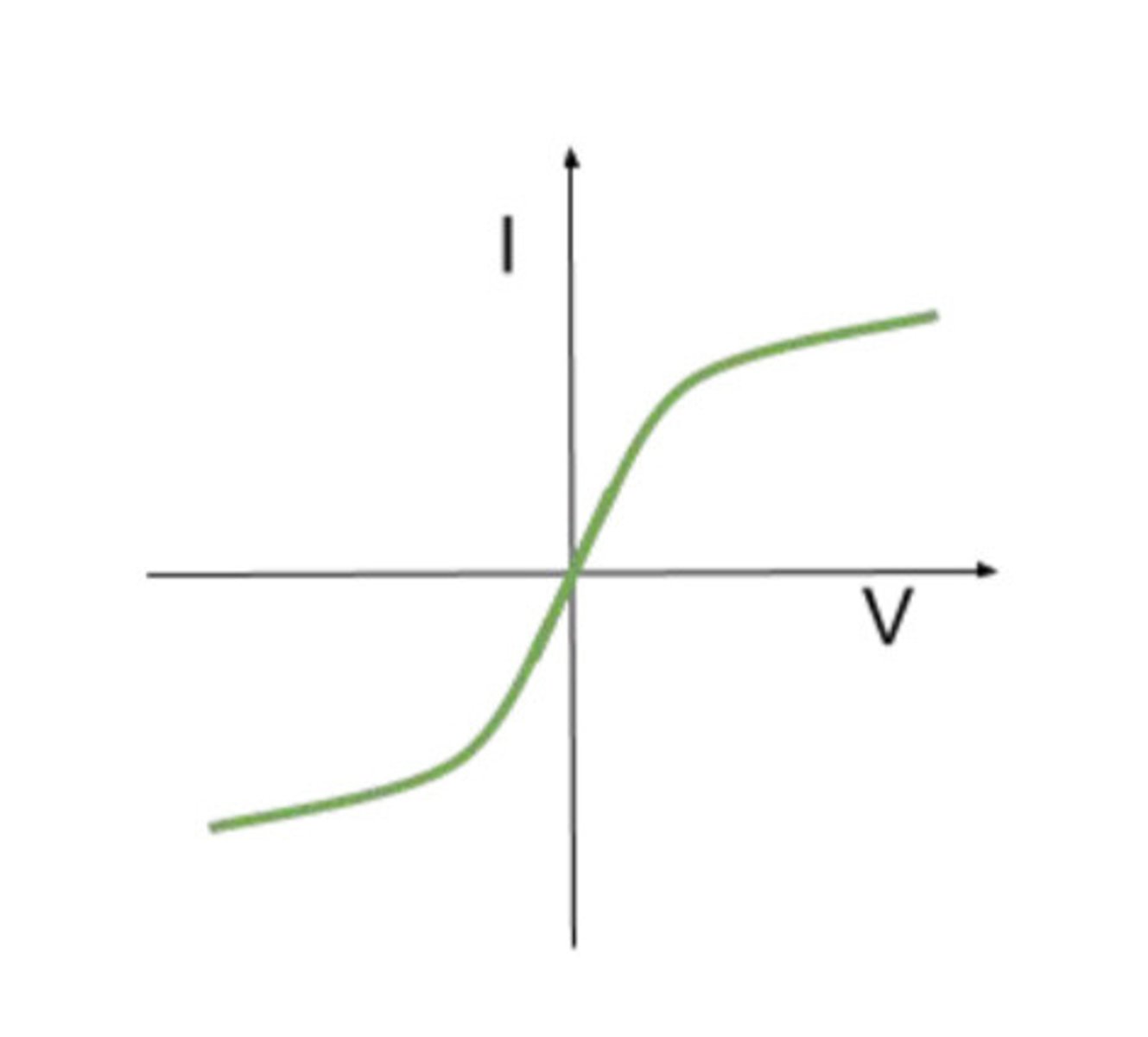
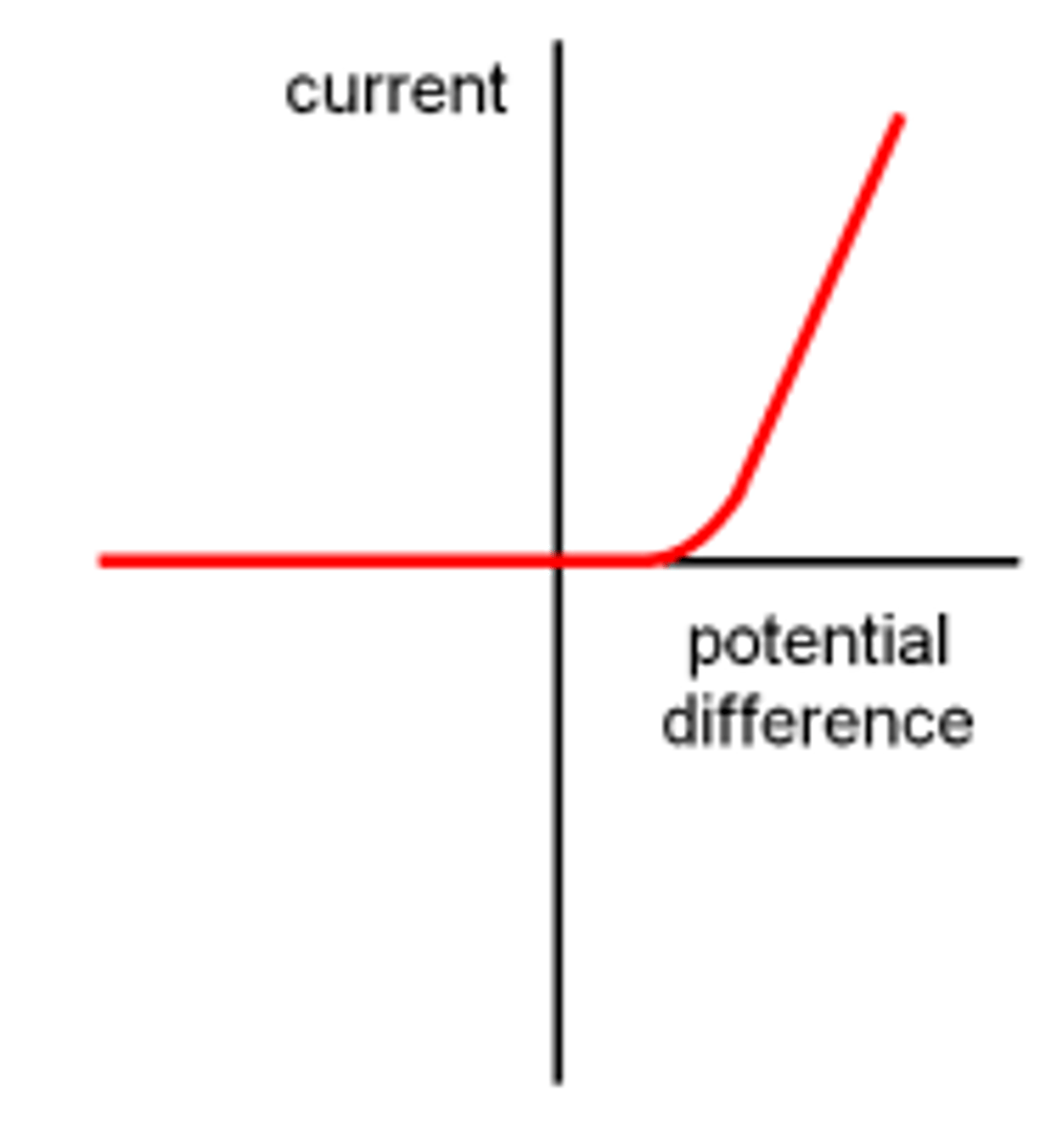
What is the IV characteristic for a diode?

Explain the IV characteristic for a filament bulb.

- The higher the current, the higher the temperature of the metal filament

- The higher the temperature, the higher the KE of the metal ions and so the more they vibrate

- This makes it harder for current to flow and so the resistance of the bulb increases

What three physical factors affect the resistance of a wire?

1. Length

2. Cross-Sectional Area

3. Resistivity

How does increasing the length of a conductor affect its resistance?

The longer the conductor is, the higher its resistance, assuming all other factors remain the same.

How does increasing the cross-sectional area of a conductor affect its resistance?

The larger the cross-sectional area of a conductor, the lower its resistance, assuming all other factors remain the same.

What is resistivity?

A characteristic property of a material that determines its resistance to current flow

Compare the resistance of two conductors of the same dimensions, but with different resistivities

The conductor with the higher resistivity, will have the higher resistance.

State the equation linking the factors affecting the resistance of a conductor.

R = ρl/ A

What equation links the number of charge carriers in a metal, along with their drift velocity, to the current flow?

I = nqvA

How does the potential vary along a uniform current-carrying wire vary as you move along it?

The potential will increase as you move along the wire

What is the electromotive force of a power supply?

The electromotive force is the amount of energy that is transferred to each Coulomb of charge that passes through it.

What is the terminal potential difference of a power supply?

The terminal potential difference of a power supply is the actual potential difference that is produced across the terminals of the supply and is provided to the circuit

Why does the electromotive forces of a supply differ from its terminal potential difference?

Some of the energy that is transferred to the charges is used to overcome the internal resistance of the power supply

Define internal resistance

The internal resistance of a power supply is the electrical resistance, when a current flows, due to the materials within the supply itself

Describe a method to determine the terminal potential difference of a battery.

Attach a voltmeter directly across the terminals of the battery when it is isolated. Since no current flows, no potential is lost due to internal resistance and so the voltmeter will read the value of the terminal p.d.

What is semiconductor?

A semiconductor is a component that can change its resistance based on external conditions.

Give two examples of semiconductors and state what they are sensitive to.

1. Thermistors are sensitive to temperature.

2. LDRs are sensitive to light.

Describe how the resistance of a thermistor changes as temperature decreased.

As temperature decreases, the resistance of a thermistor will increase.