A Level Maths - Statistics

Linear Regression

y = axⁿ

logy = loga + nlogx

Exponential Regression

y = ab^x

logy = loga + xlogb

Normal Approximation

µ = np

σ =√(np(1-p))

Mean

∑x ÷ n

GF: ∑xf ÷ ∑f

Variance

(∑x²/n) - (∑x/n)²

Standard Deviation

√variance

Histograms: Height

Area = k x frequency

Frequency Density

frequency ÷ class width

Population

Whole set of items of interest.

Census

Observes/measures every member of a population

Sample

Selection of observations taken from a subset of the population which is used to find out info about the population.

Sampling Frame

A list of individuals (named or numbered) from whom the sample is drawn

Random Sampling

Every member of the population has an equal chance of being selected

Systematic Sampling

Every nth person is chosen.

Stratified Sampling

Population is divided into mutually exclusive Strat and a random sample is taken from each.

Quota Sampling

Interviewer selects a sample that reflects the characteristics of the population

Opportunity Sampling

Choosing whoever is available

Continuous Variable

Can take any value in a given range

Discrete Variable

Takes specific values in a given range

Conditions for Binomial

Fixed no. of trials 2 possible outcomes Outcomes are independent Fixed probability of success

Probability: Independent if...

P(A∩B) = P(A) X P(B)

P(A|B) = P(A)

Probability: Mutually exclusive if...

P(A∩B) = 0

P(A∪B) = P(A) + P(B)

Conditional Probability

P(A|B) = P(A∩B)/P(B)

Probability Addition Rule

P(A∪B) = P(A) + P(B) - P(A∩B)

If there are 3 events, and A and B are mutually exclusive...

P(A∪B∪C) = P(A) + P(B) + P(C) - P(A∩C) - P(B∩C)

What is a DRV - discrete random variable

it is a random variable that can only take certain values

...

...

probability mass function

a function that gives the probability that a discrete random variable is exactly equal to some value

what does a probability distribution do

describes the probability of any outcome in the sample space

P(A/B) =

(P(A n B))

P(B)

If they are independent events P(A) * P(B) =

P(A N B)

SUM OF P(X=x) =

1

formula for probability X=r where X is the number of desired outcomes binomial distribution formula

nCr P^r * (1-p)^(n-r)

p = probability of success r = number of times you want success n= number of trials

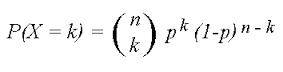
standard deviation

a computed measure of how much scores vary around the mean score

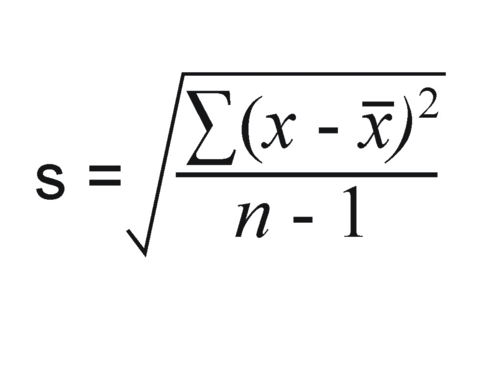
general probability addition rule

P(A∪B)=P(A)+P(B)−P(A∩B)

P(A∩B)=P(A)+P(B)−P(A∪B)

what is an event

a set of possible outcomes - not necessarily equally likely

sample space

set of all possible outcomes , all equally likely

A ∪ B

means A or B or both

A ∩ B

means both A and B

The rules for tree diagrams are

Select which branches you need Multiply along each branch Add the results of each branch needed. Make sure that you include enough working to show which branches you are using (method). Be careful to allow for selection with and without replacement.

if you are told what has happened for the first choice and need to find second you read off tree diagram

if you are told what has happened for the second choice use formula

sample space diagram

mutually exclusive events

Two events that cannot occur at the same time

what is P(A∩B) if two events are mutually exclusive

P(A∩B) = 0

Sampling units

Individual units of a population

what does a census do

observes and measures every member of a population

advantages / disadvantages of census

advantages :

gives a completely accurate result

disadvantages -time consuming and expensive -hard to process large quantity of data

advantages/disadvantages of a sample

advantages :

less time consuming and expensive than census fewer people have to respond less data to process than in a census

disadvantages

data may not be as accurate sample may not be large enough to give information about sub groups of the population

sampling frame

a list of individuals from whom the sample is drawn

population

a whole set of items that are of interest

sample

a selection of observations taken from the subset of the population which is used to find out information about the population as a whole

simple random sampling

Every sample from the population has an equal chance of being chosen

• formed by when each item given number then random number generator used or lottery

simple random sampling advantages/disadvantages

advantages

-easy and cheap to implement for small populations and small samples

• free of bias -each sample unit has a known and equal chance of selection

disadvantages

sampling frame is needed not suitable when population size/sample size is large as it would be potentially tie consuming, disruptive and expensive

3 different types of random sampling

Simple random sampling

Systematic sampling • Stratified sampling

systematic sampling

The required elements are chosen at regular intervals from an ordered list

e.g if sample size was 20 out of population of 100 you would take one out of every 5 as 100/20=5

advantages/disadvantages systematic sampling

advantages

• easy and quick to use

• suitable for large samples/populations

disadvantages

sample frame needed can introduce bias if sampling frame not random

stratified sampling

a variation of random sampling; the population is divided into mutually exclusive strata - males and females for example

and a random sample is taken from each

number sampled in a stratum/total sample size = number in stratum/number in population

advantages/disadvantages stratified sampling

advantages

• sample accurately reflects the population structure

• guarantees proportional representation of groups within a population

disadvantages

-population must be clearly classified into distinct strata -selection from strata suffers from same disadvantages as simple random sampling

quota sampling

interviewer/reasearcher selects a sample that reflects the characteristics of the whole population

quota sampling advantages/disadvantages

Advantages:

• Allows a small sample to still be representative

• No sampling frame required

• Quick, easy and inexpensive

• Allows for easy comparison between different groups within a population

Disadvantages:

• Non random sampling and so can introduce bias

• Population must be divided into groups which can be costly or inacurate

• Non responses are not recorded as such

opportunity sampling

a sample of whoever happens to be there and agrees to participate and fit the criteria looked for

opportunity sampling advantages/disadvantages

Advantages:

• Easy to carry out

• Inexpensive

Disadvantages:

• Unlikely to provide a representative sample

• Highly dependent on individual researchers

quantitive data

numerical data

qualitative data

Information describing color, odor, shape, or some other physical characteristic

continuous variable

a quantitative variable that has an infinite number of possible values that are not countable

discrete variable

variable that only have set values

class boundaries

Tell you the maximum and minimum values that belong in each class

class width

the difference between upper and lower class limits. - remember if continuous above 0.5 and below by 0.5

words to describe scatter diagrams - correlation

Strong - close points to each other Weak Positive Negative Fairly Very Extremely - how steep None

how to describe correlations in questions

• always link to question context e.g house prices go up the closer they are to the station

regression lines

The line of best fit drawn through a scatterplot

they have equation y=a + bx

b is gradient if positive then they are correlated positively if negative then negatively correlated

interpolation

estimating a value within the range of measured data

• USUALLY MORE RELIABLE

You are usually asked to give an interpretation of the gradient Eg for every 1 degree rise there will be 22 more ice creams sold per hour For every 1 minute passed the temperature will cool by 1.5 degrees For every hour passed the bacteria will have increased by 15 - does this seem right? LOOK AT THE SCALE eg 15 (million) they were in millions

extrapolation

Estimating a value outside the range of measured data.

• usually unreliable

how to identify outliers

• if it is 1.5*IQR above/below the upper/lower quartiles it is an outlier

• if it is more than 2 standard deviations from the mean it is outlier

coding - inverse function

means it is the exact inverse function e.g if the x was formed from 2y+4 you would do x-4 /2 to get x

however for standard deviation it is slightly different -if standard deviation =b was formed by 3d+8 to get the d you would just divide by 3 and not account for subtracting the 8. - However IT IS ALWAYS POSITIVE VALUE SO IF WORKING BACKWARDS IT COULD BE NEGATIVE OR POSITIVE SO YOU WOULD NEED MEAN INFORMATION TO SOLVE.

variance

standard deviation squared

binomial PD

probability of n successful

binomial CD

probability of 0-n successful cumulative

in binomial distribution for each random variable what must there be

• independent of each other

• fixed number of trials

• 2 outcomes

• fixed probability

how to find which to put on x axis

x always on top or left of graph

uniform distribution

probability of eachh event exactly same

what is trace in statistics

a specific value which is small

comparing box plots

• Compare Medians

• Compare Range (IQR)

• Compare Skew

• Put comparison into context

histograms what to know

class width * frequency density = frequency

might need to use ratios

class width shown to you

might need to see that if a certain area represents a certain frequency in a certain ratio , how you can apply this ratio to the others

need to practice this with pp

cumulative frequency tables to remember

• keep a running total

• plot against upper boundaries

• make a smooth shaped s curve

unimodal data

data with one mode

uniform data

no mode / data is symmetrical

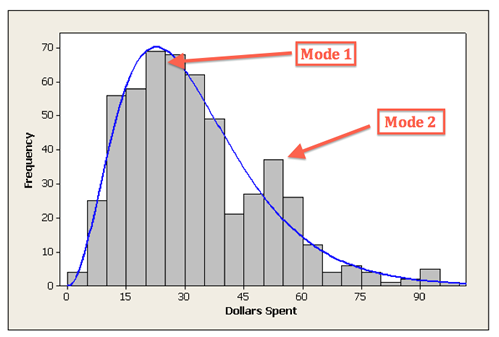
bimodal data

A histogram will have two peaks as the data has two modes.

• peaks do not have to be equal

how to interpolate data e.g find the 17th value

go across each frequency and when you find the area upon which the 17th value lies, and lets say the first category contained 10 and the next 12,

• you would do 17-10 =7 to get remainder of 7 , then do 7/12 * class width = x

• then you would add x to the starting value in the class width and that is answer

traps you could fall for interpolation

• nearest minute - make sure to get correct class width for this

mean

the arithmetic average of a distribution, obtained by adding the scores and then dividing by the number of scores

• pros uses every data item

• cons affected by extreme values

median

the middle score in a distribution; half the scores are above it and half are below it

pros - unaffected by extreme values

• could still calculate if couple data items missing

mode

the most frequently occurring score(s) in a distribution

• pros unaffected by extreme values, easy to calculate

• cons only useful if there are relatively high frequencies involved

what to remember for doing inverse functions of means and standard deviations - coding

means it is the exact inverse function e.g if the x was formed from 2y+4 you would do x-4 /2 to get x

however for standard deviation it is slightly different -if standard deviation =b was formed by 3d+8 to get the d you would just divide by 3 and not account for subtracting the 8

what is variance

How the values are dispersed around the mean; the larger the variance, the larger the dispersion of the scores

what to remember about jacksonville

really hot - most hot in southern east coast of america 23-28 degree average

what to remember about Beijing

temperature relatively high high temperature range

What to remember about Perth

temperature range similar to UK It is in Australia Has some extreme values of data - maximum rainfall 102mm Near to sea

What to remember about UK

July - August have highest temperatures 15-16th october 1987 was storm so high windspeeds rainfall etc

Heathrow is warmest Leuchars coldest

Hurn is by sea so more windy

Are there cities that have very different weather to others

beijing vs leuchars

What is UK temp range

3.8-28.7 degrees celcius