Chapter 11: Analytic Geometry

Based on Chapter 11: Analytic Geometry from the 8th edition of Algebra & Trigonometry, Enhanced with Graphing Utilities by Michael Sullivan and Michael Sullivan III. Table of Contents: Section 11.1: cards 1 - 4; Section 11.2: cards 5 - 12; Section 11.3: cards 13 - 24; Section 11.4: cards 25 - 33; Section 11.5: cards 34 - 38; Section 11.6: cards 39 - 46; Section 11.7: cards 47 - 51

Definition of circles

Definition of circles

When the plane is perpendicular to the axis of the cone when it intersects

Definition of ellipses

When the plane is tilted slightly when it intersects the cone

Definition of parabolas

When the plane is tilter farther so that it is parallel to the cone generator

Definition of hyperbolas

When the plane intersects both parts (upper and lower nappes) of the cone

Parabola

A collection of all points in a plane that are the same distance from a fixed point (focus) as they are from a fixed line (directrix)

Axis of symmetry

Imaginary line that goes through the vertex and perpendicular to the directrix

Vertex of a parabola

(-{b/2a}, f(-{b/2a}))

Directrix

A line that is ±2a units from the vertex

Focal length

The value a, the directed distance from the vertex to the focus of the parabola

Latus Rectum

A line segment that passes through the focus and is parallel to the directrix, with the length of |4a|

Characteristics of a parabola with the vertex (h, k) and a vertical axis of symmetry

1. Equation: (x-h)²=4a(y-k)

2. If a>0: opens up

3. If a<0: opens down

4. Vertex: (h, k)

5. Focus: (h, k±a)

6. Directrix: y=k±a

7. Axis of symmetry: x=h

Characteristics of a parabola with the vertex (h, k) and a horizontal axis of symmetry

1. Equation: (y-k)²=4a(x-h)

2. If a>0: opens right

3. If a<0: opens left

4. Vertex: (h, k)

5. Focus: (h±a, k)

6. Directrix: x=h±a

7. Axis of symmetry: y=k

Ellipse

A collection of all points in the plane whose distance from two fixed points is a constant sum

Center

The point on the focal axis midway between the foci

Foci

Plural of focus, the fixed points equidistance form the center and located on the focal axis

Vertices

The points where the ellipse intersects its axes

Major axis

The line connecting vertices that passes through the center of an ellipse and through its two foci with the length of 2a

Minor axis

The line between the center of an ellipse that is perpendicular to the major axis

Pythagorean relations

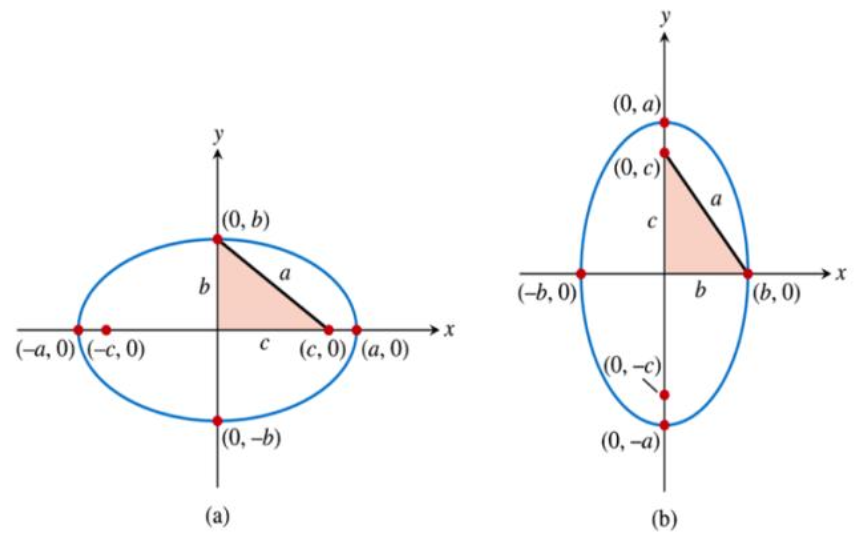
Characteristics of an ellipse with the center (0, 0) and the major x-axis

1. Equation: {x²/b²} + {y²/b²} = 1

2. Focal axis: x-axis

3. Foci: (±c, 0)

4. Vertices: (±a, 0)

5. Pythagorean relation: a²=b²+c²

Characteristics of an ellipse with the center (0, 0) and the major y-axis

1. Equation: {y²/a²} + {x²/b²} = 1

2. Focal axis: y-axis

3. Foci: (0, ±c)

4. Vertices: (0, ±a)

5. Pythagorean relation: a²=b²+c²

Characteristics of an ellipse with the center (h, k) and the major x-axis

1. Equation: {(x-h)²/a²} + {(y-k)²/b²} = 1

2. Focal axis: y=k

3. Foci: (h±c, k)

4. Vertices: (h±a, k)

5. Pythagorean relation: a²=b²+c²

Characteristics of an ellipse with the center (h, k) and the major y-axis

1. Equation: {(y-k)²/a²} + {(x-h)²/b²} = 1

2. Focal axis: x=h

3. Foci: (h, k±c)

4. Vertices: (h, k±a)

5. Pythagorean relation: a²=b²+c²

Eccentricity

e=c/a

Hyperbola

The collection of points P=(x, y) such that the distance of the distances from P to the foci is ±2a

d(F₁, P) - d(F₂, P) = ±2a

Foci

Fixed points of the hyperbola

Transverse axis

The line through the foci

Center

The point on the transverse axis midway between foci

Vertices

The points where the hyperbola intersects the transverse axis

Characteristics of a hyperbola with the center (0, 0) and transverse axis along x-axis

1. Equation: {x²/a²} - {y²/b²} = 1

2. Focal axis: x-axis

3. Foci: (±c, 0)

4. Vertices: (±a, 0)

5. Pythagorean relation: c²=a²+b²

6. Asymptotes: y = ±{b/a}x

Characteristics of a hyperbola with the center (0, 0) and transverse axis along y-axis

1. Equation: {y²/a²} - {x²/b²} = 1

2. Focal axis: y-axis

3. Foci: (0, ±c)

4. Vertices: (0, ±a)

5. Pythagorean relation: c²=a²+b²

6. Asymptotes: y = ±{a/b}x

Characteristics of a hyperbola with the center (h, k) and horizontal transverse axis

1. Equation: {(x-h)²/a²} - {(y-k)²/b²} = 1

2. Focal axis: y = h

3. Foci: (h±c, 0)

4. Vertices: (h±a, 0)

5. Pythagorean relation: c²=a²+b²

6. Asymptotes: (y-k) = ±{b/a}(x-h)

Characteristics of a hyperbola with the center (h, k) and vertical transverse axis

1. Equation: {(y-k)²/a²} - {(x-h)²/b²} = 1

2. Focal axis: x = h

3. Foci: (0, k±c)

4. Vertices: (0, k±a)

5. Pythagorean relation: c²=a²+b²

6. Asymptotes: (y-k) = ±{a/b}(x-h)

General form of a conic

1. Ax² + Cy² + Dx + Ey + F = 0; A and C cannot both equal 0

2. Defines a parabola: AC = 0

3. Defines an ellipse: AC > 0

4. Defines a hyperbola: AC < 0

5. Defines a circle: A = C

General form of a conic with rotation of axes

Ax² + Bxy + Cy² + Dx + Ey + F = 0

Coordinates for (x’, y’)

1. x’ = rcos(α)

2. y’ = rsin(α)

The angle to rotate through

cot(2θ) = {(A-C)/B}

If cot(2θ) ≥ 0: 0° < 2θ ≤ 90° and 0° < θ < 45°

If cot(2θ) < 0: 90° < 2θ < 180° and 45° < θ < 90°

Identifying conics with a rotation of axes theorem

1. Defines a parabola: B² - 4AC = 0

2. Defines an ellipse (or circle): B² - 4AC < 0

3. Defines a hyperbola: B² - 4AC > 0

Eccentricity

For any point on a conic section, the ration between the distance from the focus and the distance to the directrix

Formula for eccentricity

e = {d(P₁, F)}/{d(P₂, D)}

Eccentricity of each conic

1. Circle: e = 0

2. Parabola: e = 1

3. Ellipse: e < 1

4. Hyperbola: e > 1

Eccentricity of a hyperbola and ellipse

e = c/a

Polar equation for a conic where the directrix is perpendicular to the polar axis at a distance of p units to the left of the pole

r = {ep}/{1-ecos(θ)}

Polar equation for a conic where the directrix is perpendicular to the polar axis at a distance of p units to the right of the pole

r = {ep}/{1+ecos(θ)}

Polar equation for a conic where the directrix is parallel to the polar axis at a distance of p units above the pole

r = {ep}/{1+esin(θ)}

Polar equation for a conic where the directrix is parallel to the polar axis at a distance of p units below the pole

r = {ep}/{1-esin(θ)}

Definition of parametric curves

Let x = ƒ(t) and y = g(t), where ƒ and g are two functions defined on some interval. Then a point on a graph (x, y) can be determined by finding x = ƒ(t) and y = g(t). Essentially, (x, y) = (ƒ(t), g(t)), where t is in the domain of ƒ and g

Orientation of a parametric curve

Successive values of t that show movement

Removing the parameter

1. Choose the easiest equation

2. Solve for the parameter

3. Substitute the result for the parameter of the other equation

4. The resultant equation is the entire graph

Projectile motion

A projectile that is fired at an inclination θ to the horizontal, with an initial speed v₀, from a height h above horizontal

Projectile motion formulas

1. x(t) = (v₀cosθ)t

2. y(t) = -½gt²+(v₀sinθ)t+h

3. g = 9.8 m/sec² OR g = 32 ft/sec²