SLR 16

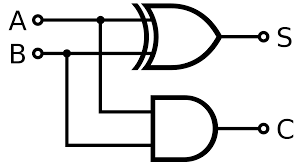
Half-Adder

takes 2 inputs and gives a two-bit output as the correct result of an addition of the two inputs

-              Logic circuit for addition

-              A  ·  B = Carry (0+0 = 0, 1+0 = 0, 0+1 = 0, 1+1 = 1)

-              A ⊕ B = Sum (0⊕0 = 0, 1⊕0 = 1, 0⊕ = 1,  1⊕1 = 0)

Half-Adder Image and Truth Table

A	+	B	=	C	S
0		0		0	0
0		1		0	1
1		0		0	1
1		1		1	0

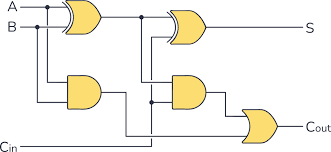
Full- Adder

combines two half adders to add three bits together, including the 2 inputs (A and B), and the carry bit C

-              A ⊕ B = D

-              A  ·  B = E

-              D ⊕ C = S

-              D  ·  C = F

-              F + E = C

Full-Adder Image and Truth Table

A	+	B	+	C(in)	+	C(out)	S
0		0		0		0	0
0		0		1		0	1
0		1		0		0	1
0		1		1		1	0
1		0		0		0	1
1		0		1		1	0
1		1		0		1	0
1		1		1		1	1

Multiple Full-Adders can be connected together

• Need 1 full adder for each bit

• Overflow errors occur when we run out of full adders

• Will add A and B and output S and C (which is carried to the next full adder)

• Next full adder will add A and B and C, and output S and C

D-type Flip-Flops

• An elemental sequential logic circuit – store one bit and flip between 2 states, 0 and 1

• Has 2 inputs – a control labelled D and a clock signal

• The clock is another type of circuit which can change state at regular time intervals

• D-type flip-flops are a positive edge-triggered flip-flop – output will only change when the clock is at a rising/ positive edge (beginning of a clock period)

• When the clock is not at a positive edge, the input value is kept and does not change

• The flip-flop circuit is important because it can be used as a memory cell to store the state of a bit