Limits and Continuity
0.0(0)
0.0(0)
Card Sorting
1/12
Earn XP
Description and Tags
Stuff to know from Unit 1
Study Analytics
Name | Mastery | Learn | Test | Matching | Spaced |
|---|
No study sessions yet.
13 Terms
1
New cards
What does continuous mean?
going on without a stop or break
2
New cards
Limit Existence Theorem
The limit as x approaches c on f(x) will exist if and only if the limit as x approaches c from the left is equal to the limit as x approaches c from the right.
3
New cards
Three Part Definition of Continuity
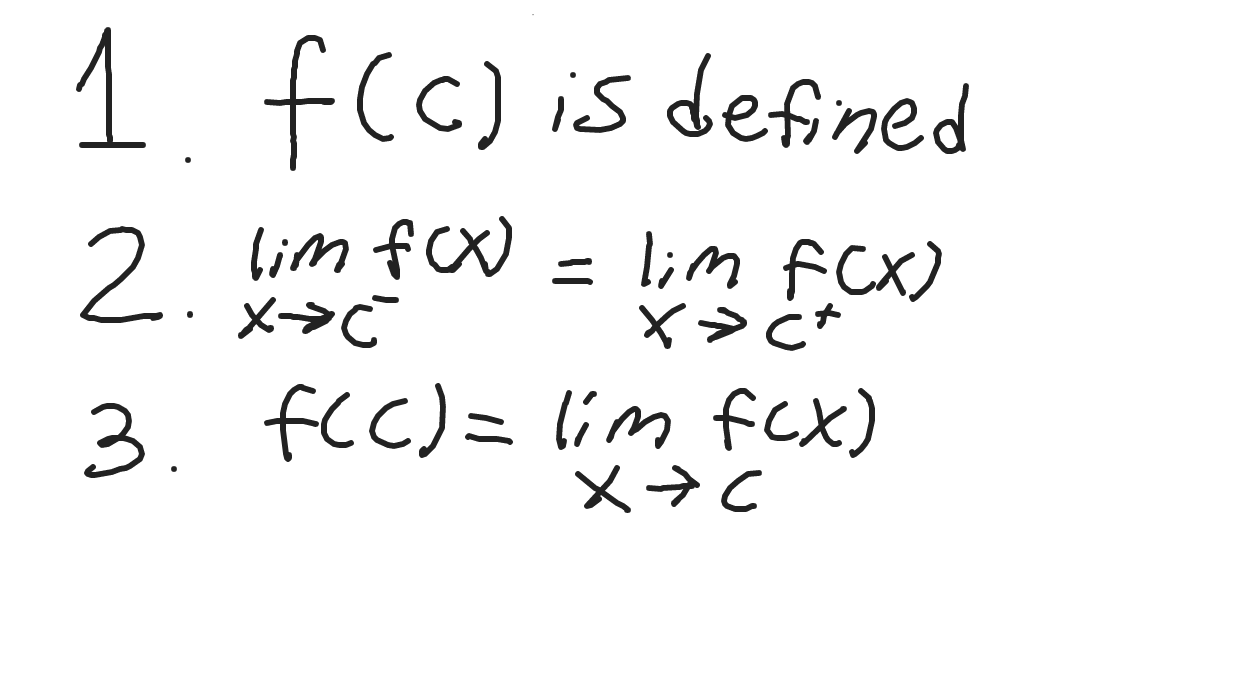
4
New cards
3 Possible limits of an exponential function?
infinity, negative infinity, Horizontal Asymptote
5
New cards
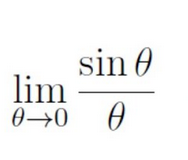
lim sincx/cx x->0
1
6
New cards
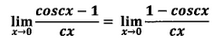
lim cos(cx) - 1 / cx x-> 0
lim 1 - coscx/cx
0
7
New cards
Intermediate Value Theorem (IVT)
if f(x) is continuous on [a, b] and f(a) < y < f(b) or f(a) > y > f(b), then there exists at least one value, x = c on (a, b) such that f(c) = y
8
New cards
IVT (laymen's term)
If the function is continuous between the x-values of a and b, then there is a x-value (c) that is between a and b (not included) with a y-value
9
New cards
Two conditions to verify IVT
1. f(x) must be continuous at [a, b]
2. f(c) must be between f(a) and f(b)
10
New cards
Infinite Limits
NOTE: Look for Vertical Asymptotes
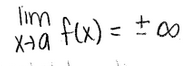
11
New cards
Limits at Infinity
Answers will be either:
End Behavior (+ - Infinity)
Horizontal Asymptotes (Number) (NOTE: rational functions have more than 1 HA)
Slant Asymptote
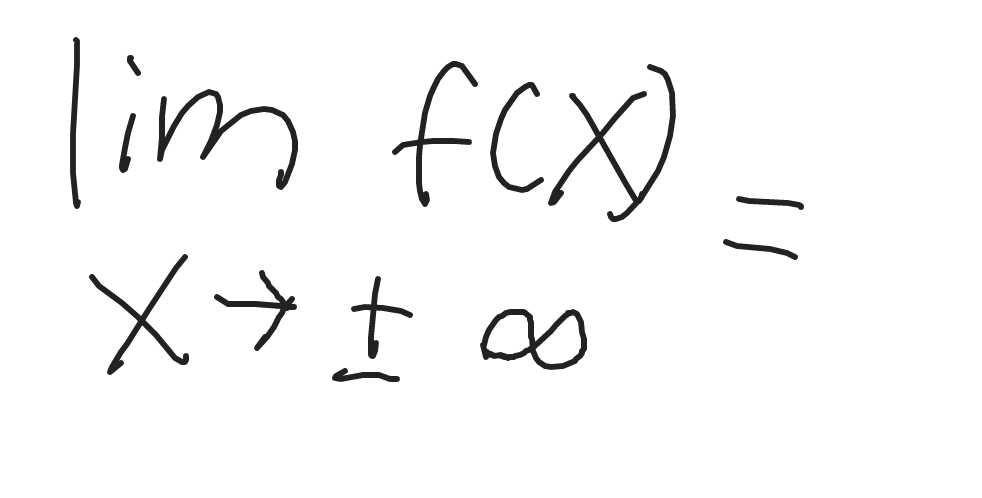
12
New cards
Justification of the existence of a Vertical Asymptote Using Limits
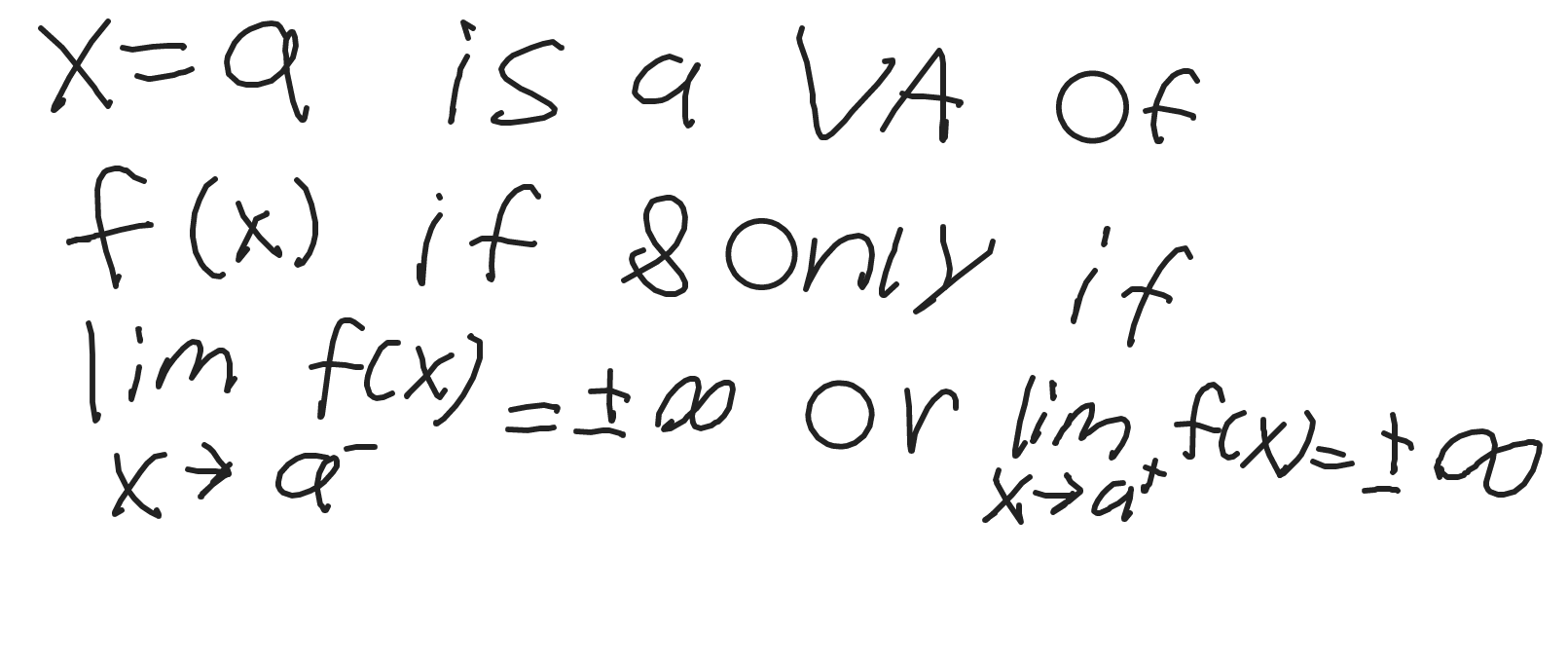
13
New cards
How to Algebraically Evaluate a limit at infinity for rational functions
Divide numerator and denominator by degree of denominator
Evaluate (Cancel out)