Calculus Review (To Cram before AP Exam)

IVT

1: f is continuous on (a,b]

2: f(a) does not equal f(b)

3. F(c) must be between f(a) and f(b)

Derivative of a^x

ln a(a^x)

Derivative of arctan

1 / (1 + x^2) & u’/1+u²

archcos

-u’/sqrt 1-u²

Archsin

u’/sqrt 1-u²

Rectangular to Polar

r²=x²+y²

R= sqrt x²+ y²

Tan (theta) = y/x —> theta= archtan y/x

Definite Integrals as Riemann Sums

Change in x= b-a/n. Xk= a+change in x(k)

Integrate a^x

a^x/ln(a) +c

Integrate tan

ln(secx)+c

Integrate csc

-ln(csc(u)+cot(u)) +c

Integrate sec

ln (sec(u) + tan(u)) +c

Integrate cot

Ln(sin(u)) +c

Integrate du/sqrt a²-u²

arcsin (u/a) +c

Integrate du/u sqrt u²-a²

1/a arcsec (u/a) +c

Integrate du/a²+u²

1/a arctan (u/a) +c

Area between two curves

integral from a to b (f(x)-g(x))dx

Volume by semi-circle cross sections

pi/8 integral from a-b [f(x)-g(x)]²dx

Volume by Square cross sections

Integral from a-b [f(x)-g(x)]²dx

Volume by Isosceles Right Triangle cross sections

Hypotenuse: ¼ integral a-b [f(x)-g(x)]²dx

Leg: ½ integral a-b [f(x)-g(x)]²dx

Volume by equilateral triangle cross sections

sqrt3/4 integral a-b [f(x)-g(x)]²dx

Volume using disks

Pi integral a-b [f(x)]²dx

Volume using washers

Pi integral a-b [(r(x))²-(r(x))²]dx

Length of a curve (arc length)

integral a-b sqrt 1+ (f’(x))²

Logistic Differential Equation: Differential Form

Kp(1-p/L)

Logistic Differential Equation: (Antiderivative) Solution

p= L/1+Ae^-kt

Logistic Differential Equation: Find A

L-p0/p0 Where p0 is the initial population

Area of a polar region

½ integral alpha-beta (r²) d/theta

Find alpha and beta by setting the equation = to 0 and solve and use smallest form of angle in radians

Parametric form of the 2nd derivative

D/dt(dy/dx)/ dx/dt

Derivative of dy/dx over dx/dt

Requirements for the Integral Test

1. F must be continuous

2. F must be positive

3. F must be decreasing

Nth term test for divergence

if lim n—> infinity an does not = 0,

Than an diverges

If lim = 0, the series may converge

Geometric Series Test

ar^n = a/1-r

Absolute value of R<1 converges

Absolute value of R> or equal 1 diverges

Root test

coverges absolutely if lim < 1

Diverges if lim >1 or infinity

Inconclusive if lim = 1

Ratio Test

Converges absolutely if lim < 1

diverges if lim >1 or infinity

Inconclusive if lim = 1

Maclaurin polynomial of sin(x)

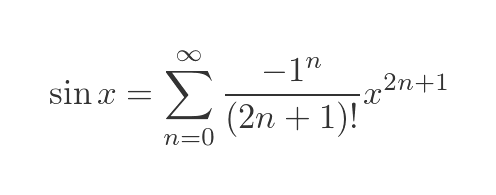
Maclaurin polynomial of Cos(x)

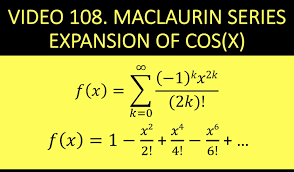
Maclaurin Polynomial of e^x

Interval of convergence???