planes, cross product, and span

plane through p with normal vector n consists of all points r such that

vector from p to r is orthogonal to n

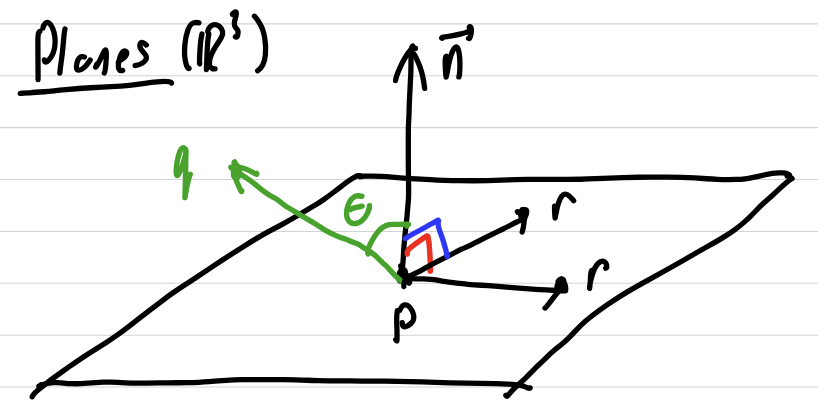
vector form of plane

n • (r-p) = 0

scalar form of plane

ax + by + cz = d

line can be described by a point p on line and a normal vector n orthogonal to line; line consists of all r such that

n • (r - p) = 0 i.e. ax + by = c

how to find parallel planes

find points p ± normalized n

planes are n • ((x y z) - p1 or p2) = 0

cross product geometrically

vector orthogonal to both u and v (that are not parallel)

-a x b =

b x a

right hand rule

curl fingers from a to b, thumb is direction of a x b

calculation of a x b = 

det ( i j k in first column | components of a in second | components of b in third)

k (a x b) =

ka x b = a x kb

a x (b + c) =

a x b + a x c

(b + c) x a =

b x a + c x a

a x a =

0

magnitude of cross product

||a||||b||sinθ

a • (a x b) =

0

b • (a x b) =

0

area of a parallelogram with sides a and b is

magnitude of their cross product

volume of parallelepiped

area of the base || a x b|| * ||c||cosθ where θ is the angle between c and a x b

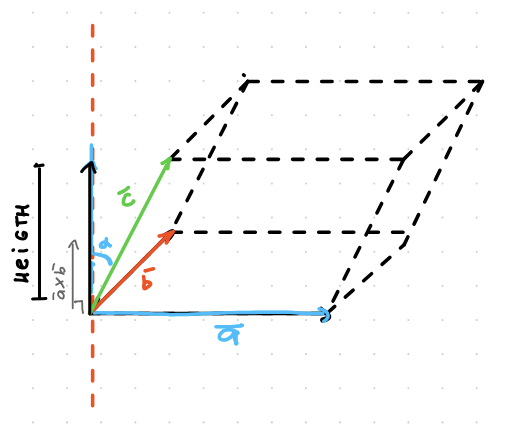
volume of parallelepiped with det

|det [ a b c ]| (the three vectors that define it)

span of vectors

all possible linear combos of those vectors

span (a, b) =

{ ta + sb | t, s are real}

span of two vectors is the xy-plane if

they are NOT collinear

span of two vectors is a line if

they ARE collinear

span of two vectors is a point if

both are zero vector

plane containing a point and a line

find line's direction vector and vector connecting point to line, cross product is plane's normal vector

equation through point perpendicular to a line

direction vector of line becomes normal vector of plane, then plug in point

vector parallel to plane intersection

cross product of two planes’ normal vectors

better volume of a parallelepiped

|a•(b x c)|