Electrostatics: Gauss's Law & Electric Potential

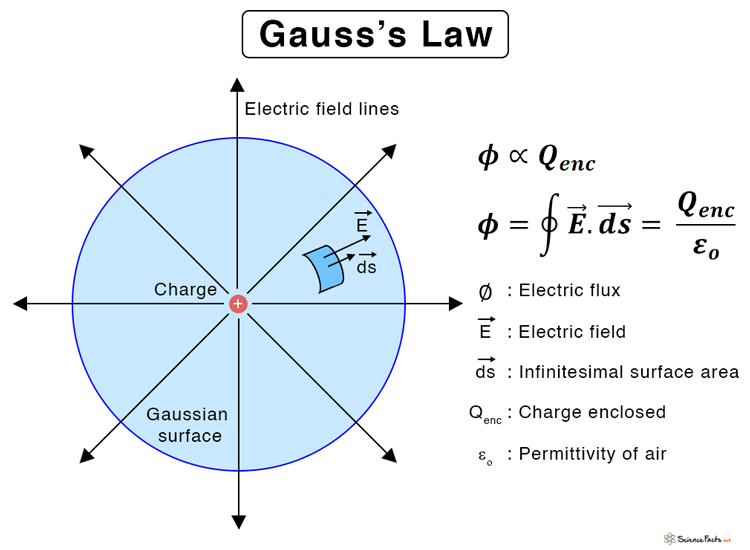
Gauss’s Law

Φ = qenc / ε₀ = ∫E · dA

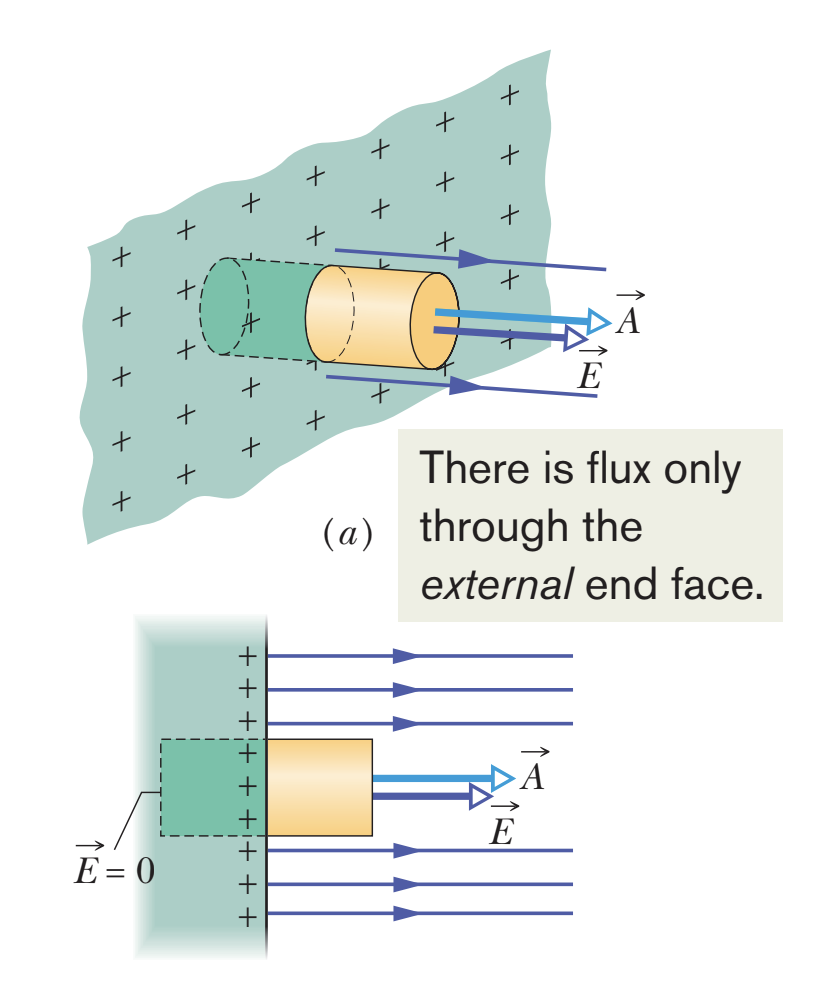
conductor

• excess charge is located entirely on the outer surfaces

• within a conductor, E = 0

field of a conducting surface

• E = σ / ε₀, directed perpendicular to surface

• Gaussian cylinder partially embedded perpendicularly into conducting surface (flux only through external end cap)

• EA = qenc / ε₀
  EA = σA / ε₀
  E = σ / ε₀

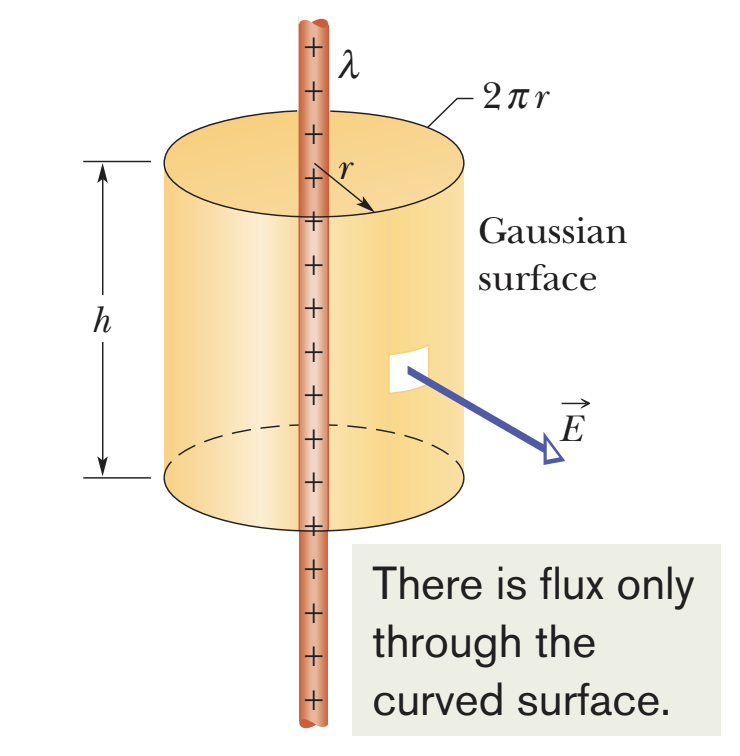
field of an infinite line of charge

• E = λ / 2πε₀r, directed perpendicular to line

• Gaussian cylinder (no flux at end caps as field only skims the surface without piercing through) = cylindrical symmetry

• EA = qenc / ε₀
  E(2πrL) = λL / ε₀
  E = λ / 2πε₀r

field of an infinite nonconducting sheet

• E = σ / 2ε₀, perpendicular to sheet

• Gaussian cylinder piercing the sheet perpendicularly (no flux at curved surface as field only skims the surface without piercing through; flux exists at both end caps) = planar symmetry

• EA + EA = qenc / ε₀
  2EA = σA / ε₀
  E = σ / 2ε₀

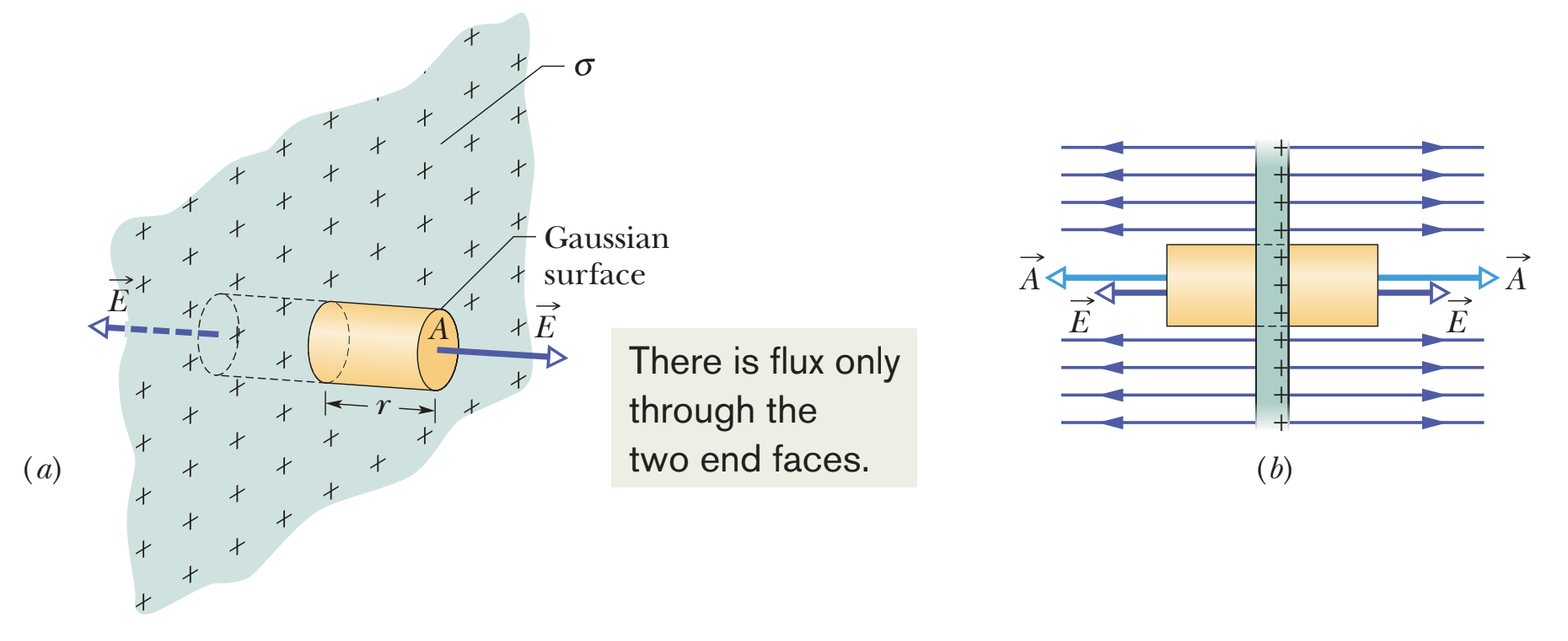
field of a spherical shell of charge

• for r ≥ R (outside shell): E = (1/4πε₀)(q / r²), directed radially → E = qenc / Aε₀ = qenc / 4πr²ε₀

• for r < R (inside shell): E = 0 → EA = qenc / ε₀ = 0

• proves shell theorems: from outside the shell, charge behaves as if located at the center of the sphere; inside the shell, E = 0 and electrostatic force from the shell on a particle = 0

field inside a uniform sphere of charge

• E = qr / 4πε₀R³, directed radially

• EA = qenc / ε₀
  E = qenc / Aε₀
  E = qenc / 4πr²ε₀ = ρVenc / 4πε₀r²

  E = (qtot / Vtot)(Venc) / 4πε₀r²
  E = (qtot / (4/3)πR³)((4/3)πr³) / 4πε₀r²
  E = qr / 4πε₀R³

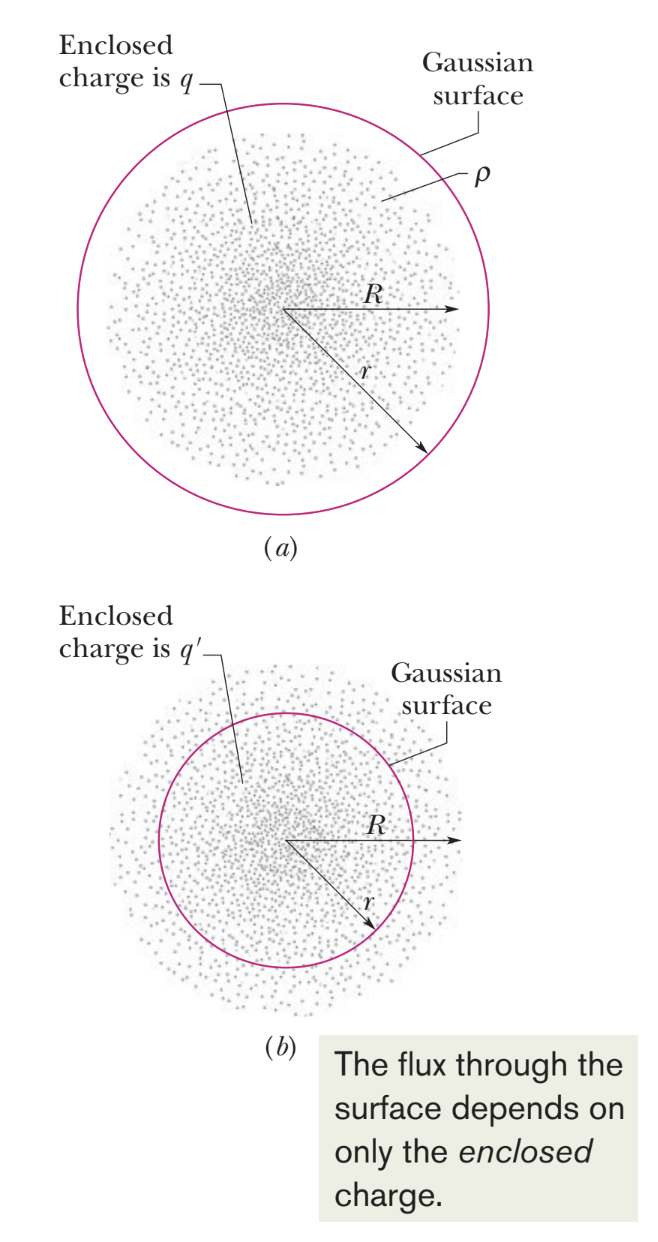
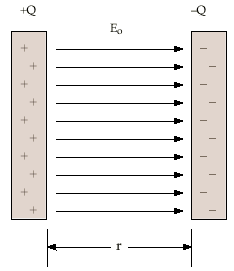
field of two conducting plates

• between plates: E = σ / ε₀, directed away from positively-charged plate toward negatively-charged plate

• to the left or right of the plates: E = 0