Geometry Midterm '22
5.0(1)
Studied by 28 people
Learn
Practice Test
Spaced Repetition
Match
FlashcardsCard Sorting
1/45
Earn XP
Study Analytics
Name | Mastery | Learn | Test | Matching | Spaced |
|---|
No study sessions yet.
46 Terms
1
New cards
Congruent
identical in form
2
New cards
Adjacent
share (a) a common side **and** (b) a common vertex
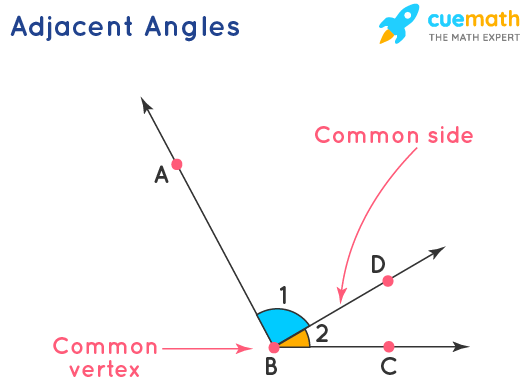
3
New cards
Complementary Angles
combines to equal 90\*
4
New cards
Supplementary Angles
combines to equal 180\*
5
New cards
Linear pair
two adjacent angles that add up to 180\*, creates a line.
6
New cards
obtuse
greater than 90 less than 180\*
7
New cards
right
90\*
8
New cards
acute
less than 90\*
9
New cards
straight
angle measure = to 180\*
10
New cards
parallel lines
same distance apart, don’t intersect, same slope
11
New cards
perpendicular lines
intersect to form 90\*, (opposite and reciprocal slope, product of their slopes is -1)
12
New cards
skew lines
dif slopes, dont intersect, exist on dif. planes
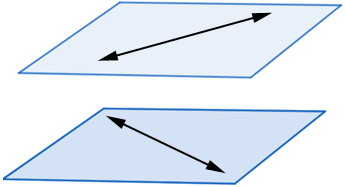
13
New cards
coplanar
exist on the same plane
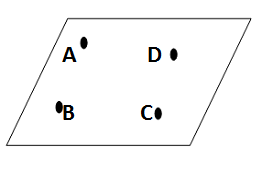
14
New cards
collinear
exist on the same line
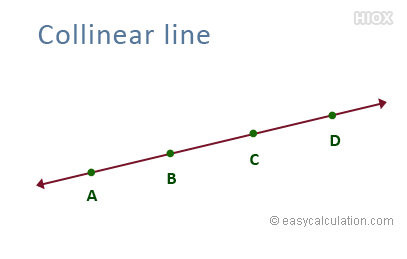
15
New cards
Whats the hypothesis (p)?
\
If charlie has an A in the class, then he never failed a test.
\
If charlie has an A in the class, then he never failed a test.
If charlie has an A in the class
16
New cards
What’s the conclusion?
\
If charlie has an A in the class, then he never failed a test.
\
If charlie has an A in the class, then he never failed a test.
then he never failed a test.
17
New cards
Converse
q → p
18
New cards
Inverse
\~p → \~q
19
New cards
Contrapositive
\~q → \~p
20
New cards
Inductive reasoning
specific observation → pattern recognition → general conclusion
21
New cards
Deductive reasoning
existing theory → formulate hypothesis → collect data → analyze data → do/don’t reject hypothesis
22
New cards
2-point postulate
**Through any two points there exists exactly one line.**
23
New cards
Line-point postulate
a line contains at least 2 points
24
New cards
Line intersection
if 2 lines intersect, then their intersection is exactly one point
25
New cards
3-point
**Through any three noncollinear points, there exists exactly one plane.**
26
New cards
Plane point
A plane contains at least three noncollinear points.
27
New cards
plane line
If two points lie in a plane, then the line containing them lies in the plane.
28
New cards
plane intersection
**If two planes intersect, then their intersection is a line.**
29
New cards
parallel postulate
If there is a line and a point not on the line, then there is exactly one line through the point parallel to the given line.
30
New cards
perpendicular postulate
**If there is a line and a point not on the line, then there is exactly one line through the point perpendicular to the given line.**
31
New cards
addition property of equality
if a = b, then a + c = b + c.
32
New cards
subtraction property of equality
if a = b, then a - c = b - c.
33
New cards
multiplication property of equality
if a = b, then a x c = b x c.
34
New cards
division property of equality
if a = b, then a / c = b / c.
35
New cards
Substitution Property of Equality
if a = b, then a can be substituted for b (or b for a) in any equation or expression.
36
New cards
Distributive property
sum: a(b + c) = ab + ac
difference a(b-c) = ab - ac
difference a(b-c) = ab - ac
37
New cards
reflexive property
a = a; a number is always equal to itself
38
New cards
symmetric property
if a = b, then b = a; values on either side of the equal sign are equal and will remain equal if the sides are flipped
39
New cards
transitive property
If a = b and b = c, then a = c.
40
New cards
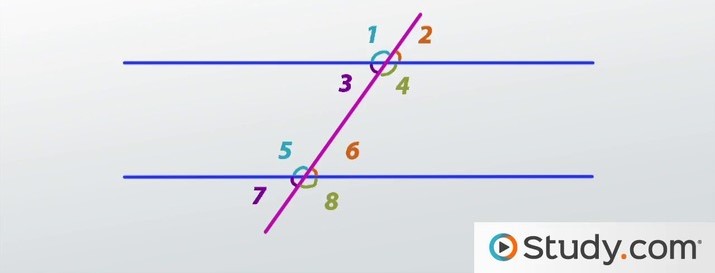
corresponding angles:
1-5
2-6
4-8
3-7
2-6
4-8
3-7
41
New cards
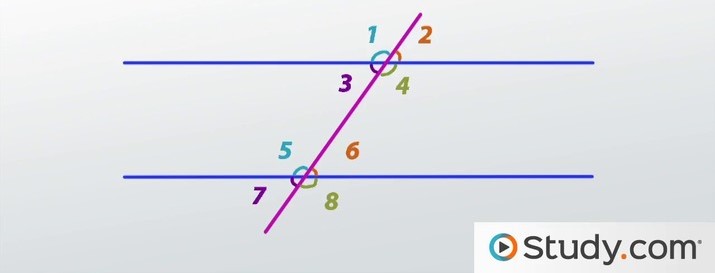
alternate interior angles:
4-5
3-6
3-6
42
New cards
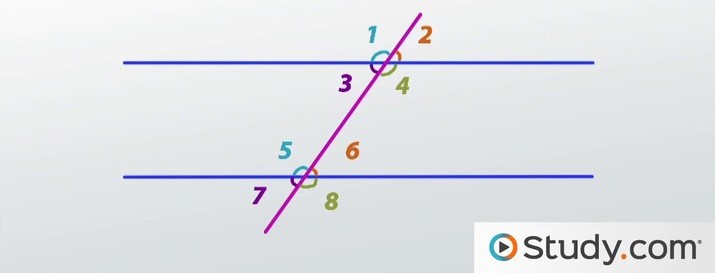
alternate exterior angles:
1-8
2-7
2-7
43
New cards
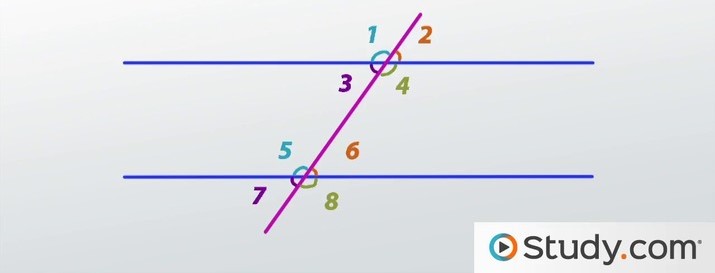
consecutive interior angles:
4-6
3-5
3-5
44
New cards
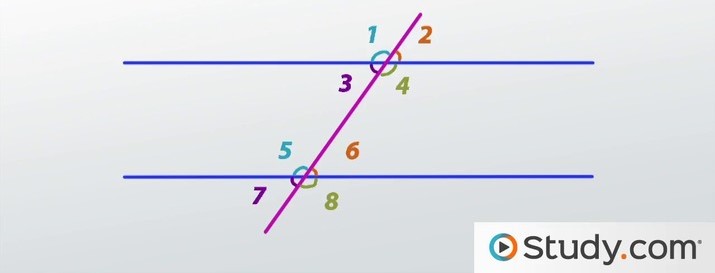
linear pairs:
1-2
2-4
4-3
3-1
5-6
6-8
8-7
7-5
2-4
4-3
3-1
5-6
6-8
8-7
7-5
45
New cards
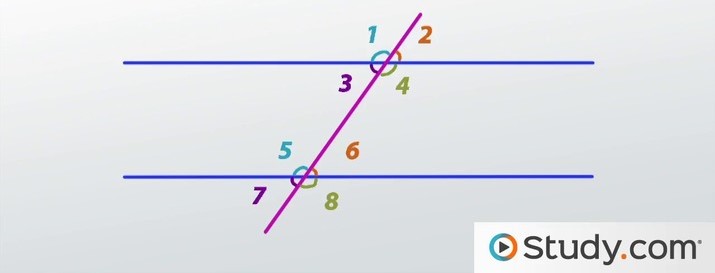
vertical angles:
1-4
2-3
5-8
6-7
2-3
5-8
6-7
46
New cards
reflections:
y-axis
x-axis
y=m
y=-m
y-axis
x-axis
y=m
y=-m
1. (-x,y)
2. (x,-y)
3. (y,x)
4. (-y,-x)
Note 
Flashcards (63)