Hell is Made of Circles

Circle

The set of all points in a plane that are equidistant from a fixed point called the center

Radius

A segment that joins the center to a point on the circle

Diameter

A chord that passes through the center of the circle (Twice the radius)

Congruent Circles

Two circles are congruent if they have the same radii

Cocentric Circles

Two or more coplanar circles with the same center

Exterior of a Circle

A point on a circle if its distance from the center is greater than the radius

Interior of a Circle

A point inside a circle if ts distance from the center is less than the radius

On the Circle

A point on a circle if tis distance from the center is equal to the radius

Tangent

A line intersecting the circle at exactly one point

Secant

A line intersecting the circle in exactly two points

Tangent Radius Theorem

A tangent line is perpendicular to the radius drawn at the point of tangency

Tangent Radius Theorem Converse

A line perpendicular to a radius at its outer end point, then it is a tangent to the circle

Central Angle

An angle whose vertex is at the center of the circle

Arc

Consists of two points on a circle and all points on that needed to connect the points by a single path. The center of the arc is the same center of the circle

Minor Arc

The shortest arc connecting two endpoints on a circle

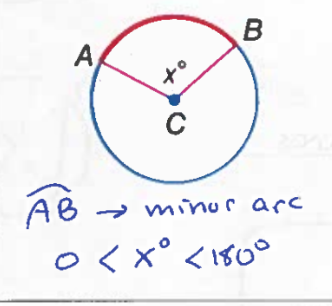
Major Arc

The longest arc connecting two endpoints on a circle

Semicircle

An arc where its endpoints lie on the diameter

Congruent Arcs

Two arcs are congruent whenever they have the same measure and are parts of the same circle or congruent circles

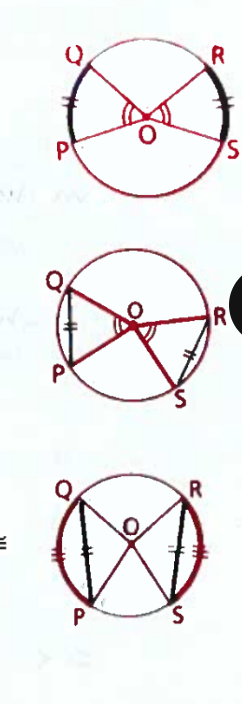
Relating Chords, Arcs, and Central Angles

If two central angles are congruent, then the chords and arcs are also congruent; converse is also true

Chord

A segment joining any two points on the circle

Chord Theorem 1

If a radius is perpendicular to a chord, then it bisects the chord.

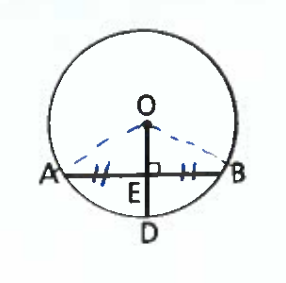
Chord Theorem 2

If a radius of a circle bisects a chord that is not a diameter, then it is perpendicular to that chord

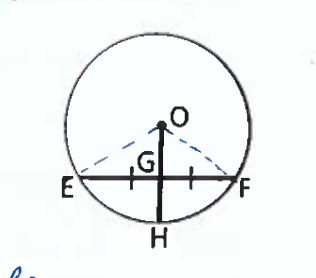
Chord Theorem 3

The perpendicular bisector of a chord passes through the center of the circle

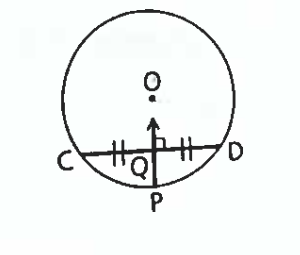
Chord Theorem 4

If two chords of a circle are equidistant from the center then they are congruent

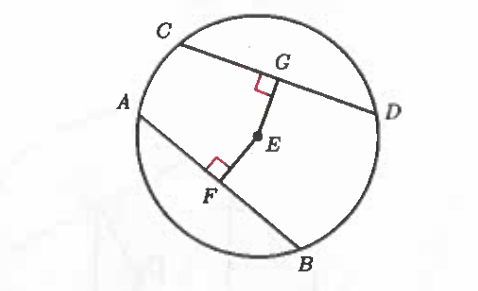
Chord Theorem 4 Converse

If two chords of a circle are congruent, then they are equidistant from the center

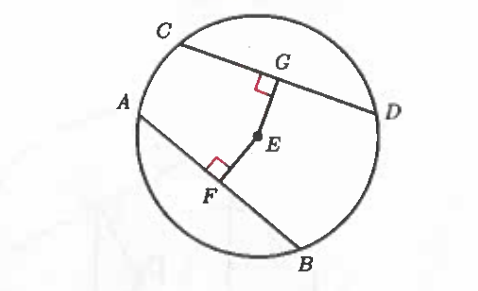
Common Tangent

A line tangent to two circles

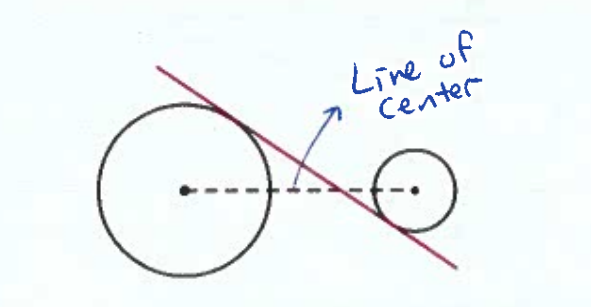
Common Internal Tangent

Crosses the Line of Centers

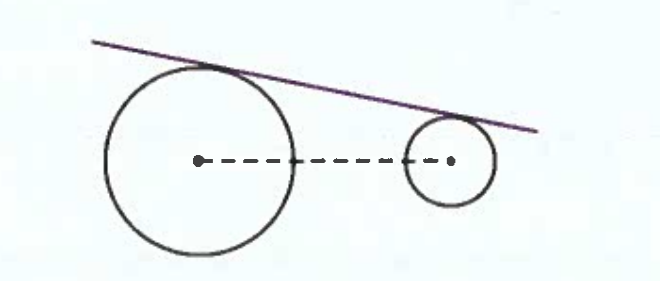
Common External Tangent

Does not cross Line of Centers

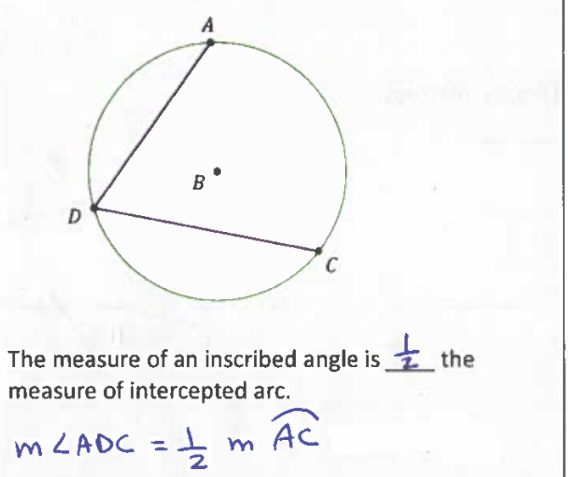
Inscribed Angle

The measure of an inscribed angle is ½ the measure of intercepted arc

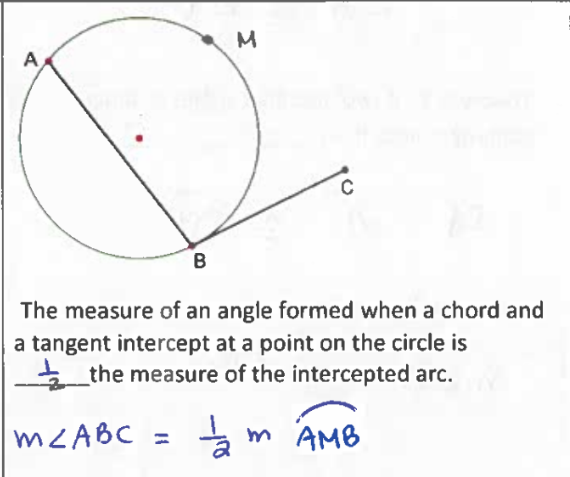
Tangent-Chord Angle or Tangent Secant Angle

The measure of an angle formed when a chord and a tangent/secant intercept at a point n the circe is ½ the measure of the intercepted arc

Angles with Vertices on the Circle - Therom 1

An angle inscribed in a semicircle is a right angle

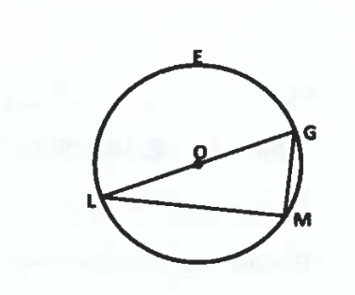
Angles with Vertices on the Circle - Therom 2

If two inscribed angles or tangent-chord angles intercept the same arc, then they are congruent

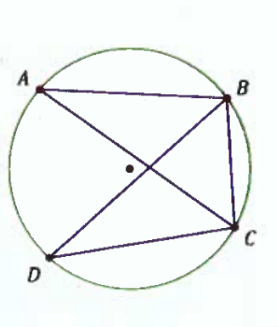
Angles with Vertices on the Circle - Therom 3

If two inscribed angles or tangent-chord angles intercept congruent arcs, then the angles are congruent

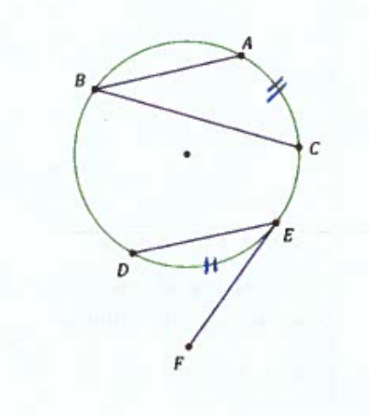
Angles with Vertices Inside but not at the Center of a Circle

The measure of a chord-chord angle is one-half the sum of the measures of the arcs intercepted by the chord-chord angle

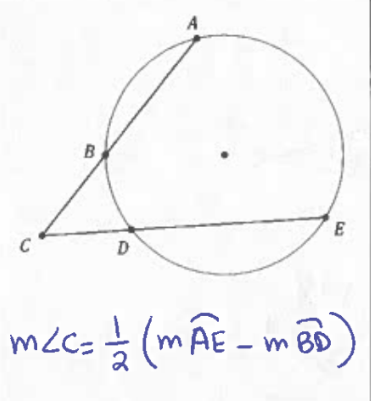
Secant-Secant Angle

measure of angle c = 1/2(measure of arc AE - measure of arc BD)

Seacant-Tangent Angle

measure of angle c = 1/2(measure of arc AE - measure of arc AD)

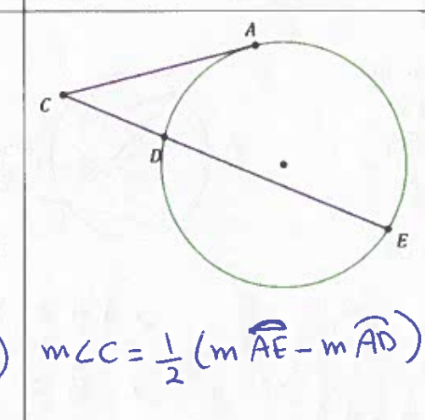
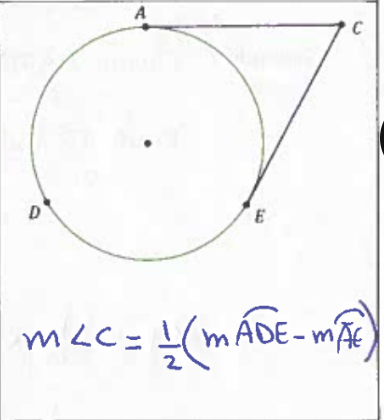
Tangent-Tangent Angle

measure of angle c = 1/2(measure of arc ADE - measure of arc AE)

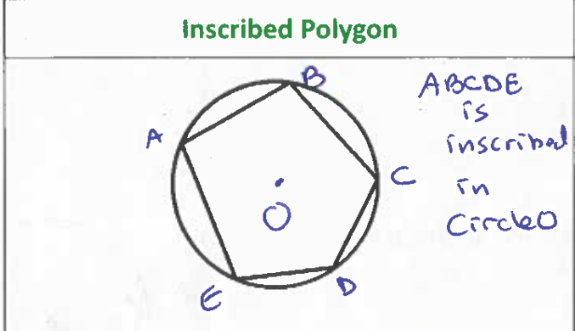
Inscribed Polygon

All vertices lie on the circle

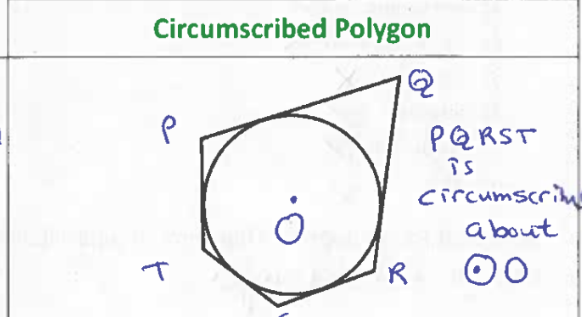
Circumscribed Polygon

Each of its sides are tangent to the circle

Circumcenter

Center of a circle circumscribed about a polygon

Incenter

Center of a circle inscribed in the polygon

Inscribed Quadrilateral Theorem

If a quadrilateral is inscribed in a circle, then its oposite angles are supplementary

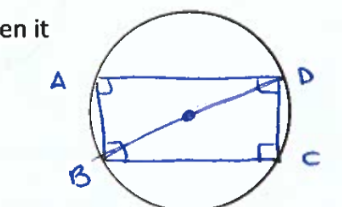
Inscribed Parallelogram Theorem

If a paralelogram is inscribed in a circle, then it must be a rectangle

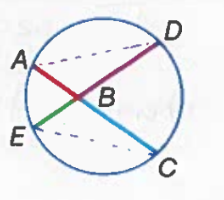
Chord-Chord Power Theorem

If two chords of a circle intersect inside the circle, then the product of the measures of the segments of one chord is equal to the product of the measures of the segments of the other chord.

Tangent-Secant Power Theorem

If a tangent and a secant intersect in the exterior of a circle, then the square of the measure of the tangent is equal to the product of the measures of the secant and its external secant segment.

Secant-Secant Power Theorem

If two secants intersect in the exterior of a circle, then the product of the measures of one secant segments and its external secant segment is equal to the product of the measures of the other secant and its external measure.

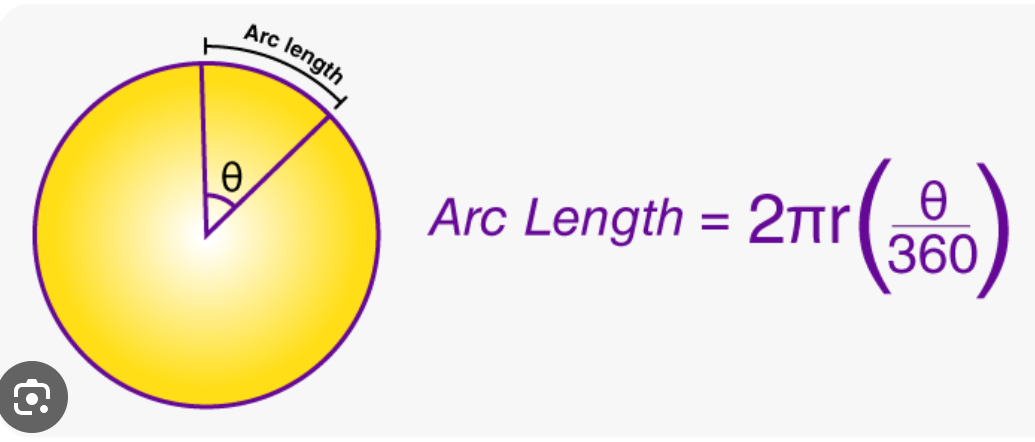
Arc Length

2pieR(0/360)