Geometry Unit 6 Conjectures
5.0(1)
5.0(1)
Card Sorting
1/13
Earn XP
Description and Tags
Study Analytics
Name | Mastery | Learn | Test | Matching | Spaced | Call with Kai |
|---|
No study sessions yet.
14 Terms
1
New cards
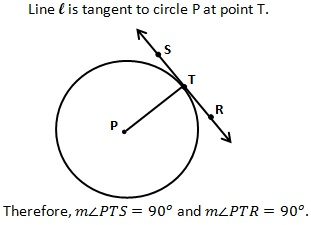
Tangent Conjecture
a tangent to a circle is perpendicular the radius is drawn to the point of tangency
2
New cards
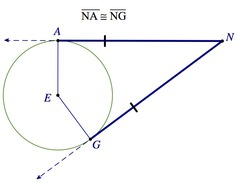
Tangent Segment Conjecture
Tangent segments to a circle from a point outside the circle are congruent
3
New cards
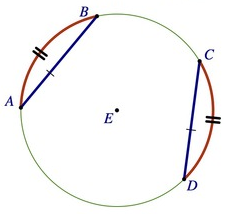
Chords Arc Conjecture
If 2 chords in a circle are congruent then their intercepted arcs are congruent
4
New cards
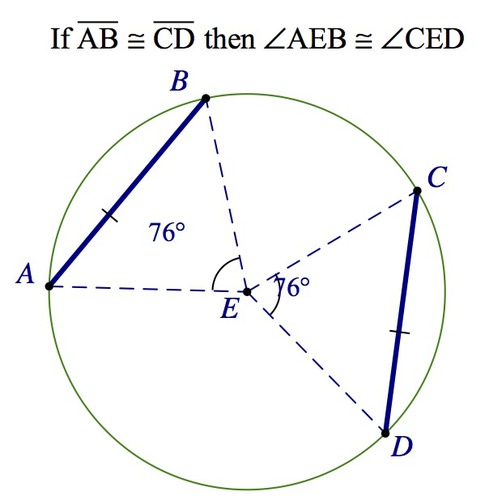
Chord Central Angles Conjecture
If 2 chords in a circle are congruent, then they determine 2 central angles that are congruent
5
New cards
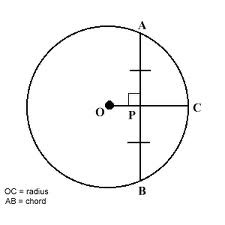
Perpendicular to a Chord Conjecture
the perpendicular from the center of a circle to a chord is the bisector of the chord
6
New cards
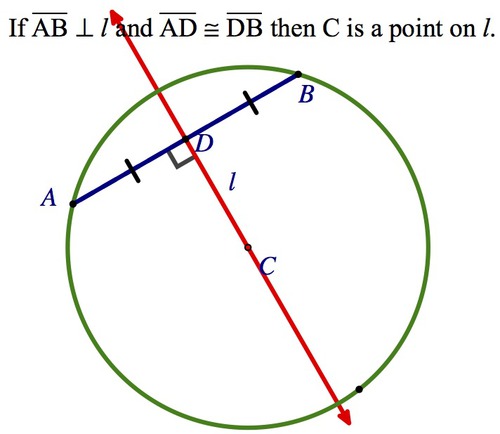
Perpendicular Bisector of a Chord Conjecture
The perpendicular bisector of a chord passes through the center of a circle
7
New cards
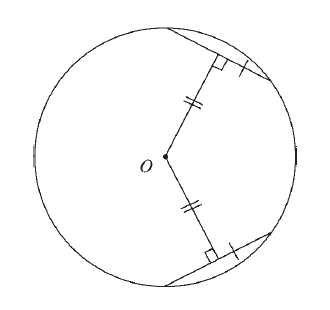
Chord distance to center conjecture
2 congruent chords in a circle are equidistant from the center of the circle
8
New cards
Inscribed Angle Conjecture
the measure of an angle inscribed in a circle is 1/2 the measure of the intercepted arc
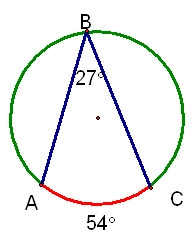
9
New cards
Inscribed Angles Intercepting Arcs Conjecture
Inscribed angles that intercept the same arc are congruent
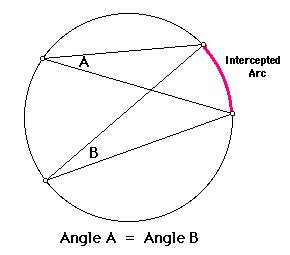
10
New cards
Angles Inscribed in a Semicircle Conjecture
Angles inscribed in a semicircle are right angles
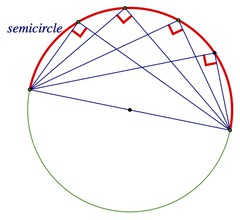
11
New cards
Cyclic Quadrilateral Conjecture
The opposite angles of a cyclic quadrilateral are supplementary
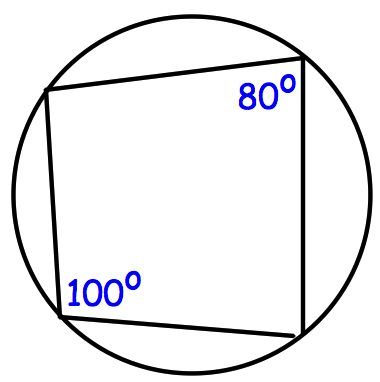
12
New cards
Parallel Lines Intercepted Arcs Conjecture
Parallel lines intercept congruent arcs on a circle
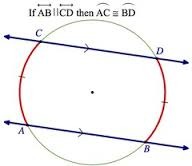
13
New cards
Circumference Conjecture
If C is the circumference and D is the diameter of a circle, then there is a number π such that C\=dπ. If d\=2r where R is the radius, then C\=2πr
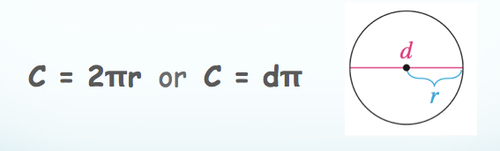
14
New cards
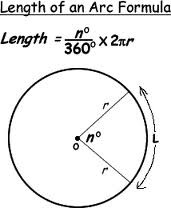
Arc Length Conjecture
The length of an arc equals the measure of the arc divided by 360 times the circumference