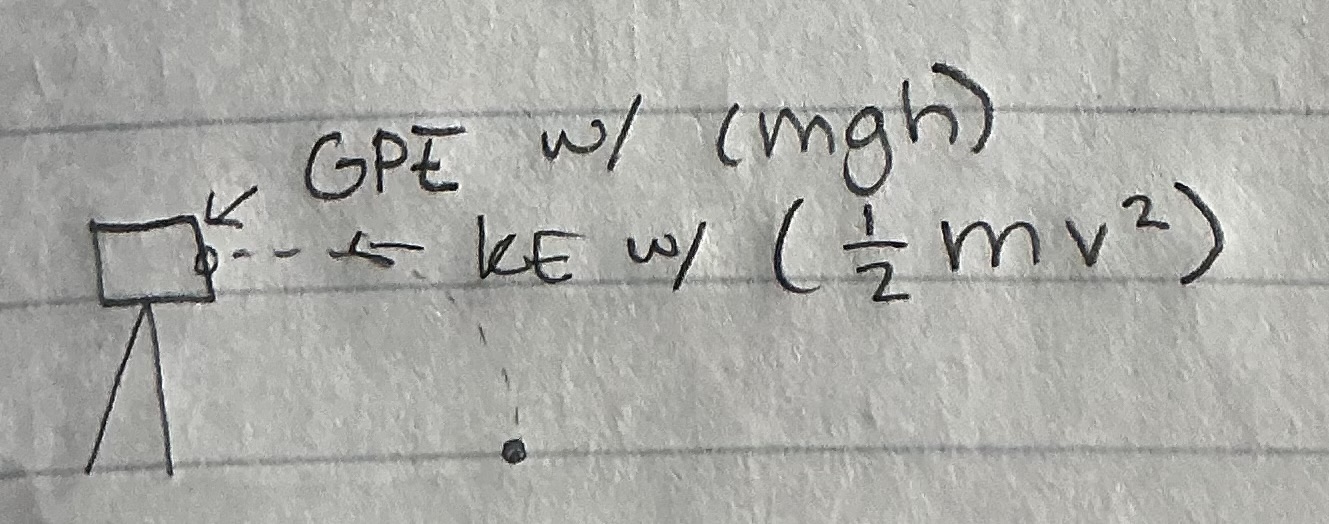AP Physics 1 Full Review (Unit 7 - Unit 8)

Hooke’s Law

F_s = -kΔx

Equilibrium point on a spring is _

Where it rests when F_NET = 0

Simple Harmonic Motion (SHM)

• Special case of periodic motion with a restoring force pulling back to equilibrium

Restoring Force

Force causing the net acceleration (for a spring —> spring force)

Equation for restoring force for a spring

-kΔx = ma

What is the restoring force for a pendulum?

Force of the earth

Restoring force is proportional to __

Distance from equilibrium point

Frequency

Number of cycles that happen in a given time period (Hertz Hz) (Cycles per second)

Period (T)

f = 1/T

How much time passes for one cycle

Period relationship with length, mass, and gravity (Pendulum)

• As length increases, so does the period

• As mass increases, the period remains constant

• As gravity increases, the period decreases

Equation for period of a pendulum

T_p = 2π Square root(l/g)

l = length

Period relationship with mass, spring constant, and gravity (Spring)

• As mass increases, the period increases

• As k increases, the period decreases

• As gravity increases, the period remains constant

Equation for Period of a Mass-Spring System

T_s = 2π Square root(m/k)

Ideal Pendulum

0 friction

Linear action makes slope __

useful in some way usually

SHM Features

1) Energy conserved

2) Restoring force = unbalanced force acting towards equilibrium

3) Object equation = x = Acos(2πft)

Object’s position in SHM equation

x = A cos(2πft)

A = Amplitude

f = Frequency

t = time

When acceleration is changing, use __

Energy

Spring max Potential Energy equation

U_{s max} = ½ kA²

Where there is no kinetic energy and it’s at amplitude position

Kinetic Energy is ___ when at the equilibrium of a vertical spring

Greatest

Energy of a pendulum equation

E_P = ½ mv² + mgh

Energy of a horizontal spring equation

E_hs = ½ mv² + ½ kx²

Energy of a vertical spring equation

E_vs = ½ mv² + ½ kx² + mgh

Equation for mechanical energy

ME = K + U

K = Kinetic Energy

U = Potential Energy

Conservation of Energy

Ballistic Pendulum

Bullet shot into a block to make it swing

• Increase Speed, increase Amplitude, Period stays constant

Volume

• Space occupied

• Measured with graduated cylinder

• V = lwh

Density (ρ)

• Amount of matter per space

• Measured with Hydrometer (or calculated)

• ρ = m/v

Weight

• Force of gravity on object (N)

• Measured with spring scale

Extensive properties definition

Properties that depend on the amount of matter (m, V, w)

Intensive properties definition

Properties that depend on type of matter (density (ρ))

Fluid states of matter

Liquid and gas

Liquid properties

• Mass, volume, and density constant

• Shape is variable

Equation for density (ρ)

ρ = m/v

units: kg/m³

Gas properties

• Mass constant

• Volume, density, shape = variable

Common density values

Air: ½ kg/m³

Water: 1000 kg/m³

Salt Water: 1030 kg/m³

Slope of a m vs. V graph

Density (ρ)

Pressure equation

P = F/A

Pressure = Force per Area

Units: N/m² = Pascal (Pa)

SCALAR

Atmospheric Pressure

1.0 × 10^5 Pa

Atmosphere puts __ on water

Pressure

Equation for pressure exerted by a fluid

P = P₀ + ρgh

P = Absolute pressure (Pa)

P₀ = Atmospheric Pressure (Pa)

ρ = Fluid density (kg/m³)

g = GFS (N/kg) —> for MCQs use g=10

h = Fluid depth (m)

Gauge Pressure

ρgh = gauge pressure (Pa)

ρ = fluid density

Archimedes’ Principle

Buoyant Force = weight of displaced fluid

Equation for Buoyant Force (F_b)

F_b = ρVg

ρ = density of fluid

V = Volume of fluid displaced

Change in pressure equation (ΔP_BA)

ΔP_BA = ρgd

Buoyant Force is caused by __

Difference in Pressure

Floating definition

Stationary with F_b = F_g

Ratio between V and ρ of a cube and water

V_W/V_c = ρ_c/ρ_W

Tells how much of cube is submerged

Ex) 40% submerged = 400 (kg/m³) / 1000 kg/m³)

Conservation Laws (Fluids) for mass and energy

Mass: Continuity Equation

Energy: Bernoulli’s Principle

Conservation of Mass (Fluid)

Same amount must pass through a point per second (speed can change)

Volume and Mass of liquid system conserved

Fluid Flow Rate Q = Volume/time

Ideal Fluid

Water assumed to be incompressible

Fluid Flow Rate (Q)

Q = Volume/Time (m³/s)

Continuity Equation

A₁V₁ = A₂V₂

A - Cross-sectional area

What kind of fluids can be used with Continuity Equation

Ideal/Incompressible fluids

Bernoulli’s Equation Relationships

• As Cross section decreases, Speed increases and Pressure decreases

• As Vertical position increases (down), Pressure increases

Bernoulli’s Equation

P₁ + ρgy₁ + ½ ρV₁² = P₂ + ρgy₂ + ½ ρV₂²

Statement of Conservation of Energy

Pressure as pipe goes up and narrows

A₁v₁ = a₂V₂

P₁ > P₂

Pressure as pipe goes down and widens

A₁ < A₂

V₁ > V₂

P₁ < P₂

Torricelli’s Theorem definition

Specific application of Bernoulli’s Equation

Container with a hole at a specified location at a specified height that sends fluid in projectile motion

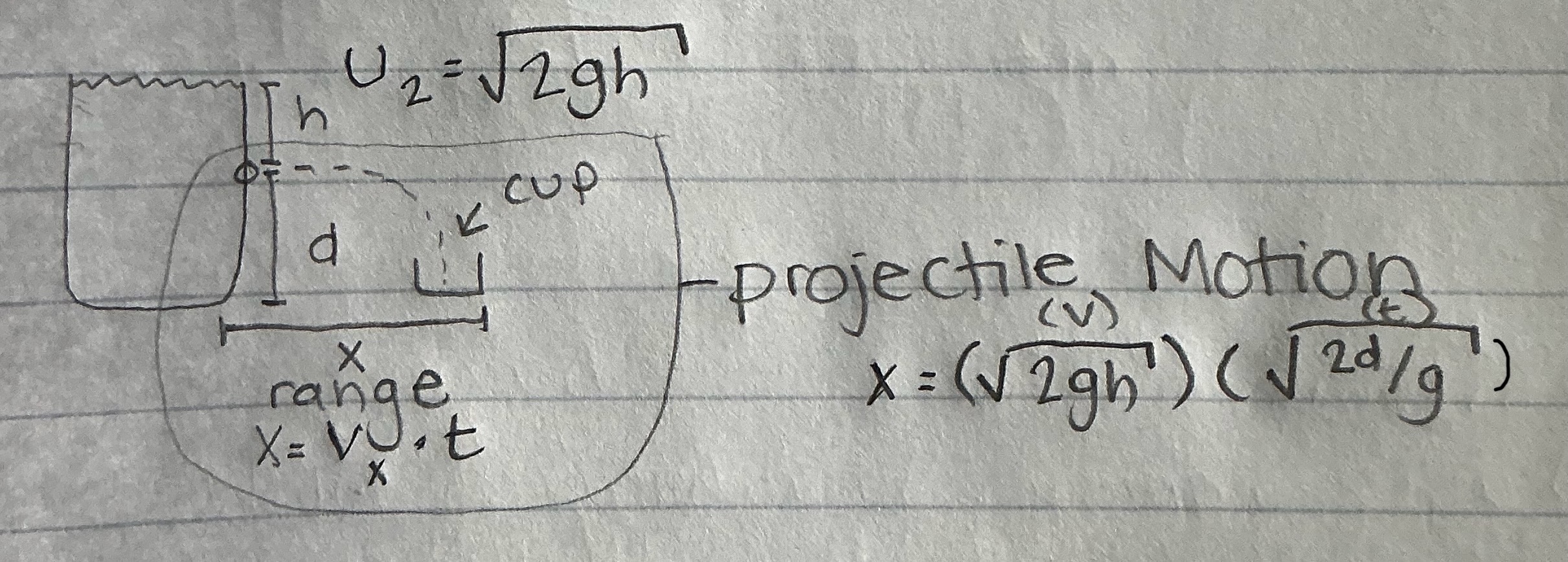
Torricelli’s Theorem

P₁ + ρgy₁ + ½ ρv₁² = P₂ + ρgy₂ + ½ ρv₂²

v = velocity

v₂ = Square root(2gΔy)