3.01-3.07 Longitudinal/Transverse Waves + Wave Speed + Frequency

Degree (°)

Unit for measuring angles

Hertz (Hz)

Unit for measuring frequency

1 Hz = 1 complete cycle per second

Meter (m)

Unit for measuring length

Meter/second (m/s)

Unit for measuring speed and/or velocity

Second (s)

Unit for measuring time

Wave

Vibrations that transfer energy and information without transferring matter

Oscillation

Vibration; repeated back-and-forth movement between any 2 states and/or positions of an object due to its displacement from its equilibrium

Transverse wave

Waves that vibrate or oscillate perpendicular to the direction of energy transfer

• Particle oscillations ⟂ to energy transfer’s direction

• Energy transferred in same direction as wave motion

• Energy transferred but particles of the medium are not

• Particles of the medium are not displaced and not transferred (although they move, they are not displaced because the particles move back and forth along the same axis/line so always return to their original position → hence the displacement of 0)

• Waves can move in solids and on the surface of liquids, but cannot move inside liquids or gases

• Some transverse waves (e.g. electromagnetic waves) can move in solids, liquids, gases, and vacuum

Examples of transverse waves

• Light waves

• Electromagnetic waves (e.g. radio, light, X-rays)

• Ripples on surface water

• Vibrations on guitar string (or vibrations on any string instrument)

Longitudinal wave

Waves where the points along its length vibrate parallel to the direction of energy transfer

• Particle oscillations are // to energy transfer’s direction

• Energy transferred in same direction as wave motion

• Energy transferred but particles of the medium are not

• Particles of the medium are not displaced and not transferred because the particles move back and forth along the same axis so always return to their original position → hence the displacement of 0)

• Can move in solids, liquids, and gases

• Cannot move in vacuum because there are no particles

Examples of longitudinal waves

• Sound waves

• Pressure waves caused by repeated movements in a fluid (liquid or gas)

• Shockwaves (e.g. some seismic waves)

Seismic wave

Waves that travel through or over Earth and which are generated by movement of the Earth’s tectonic plates

Transverse wave VS longitudinal wave

• Structure

  • Transverse → peaks/crests and troughs

  • Longitudinal → rarefactions and compressions

• Vibration

  • Transverse → ⟂ to energy transfer’s direction

  • Longitudinal → // to energy transfer’s direction

• Vacuum

  • Transverse → only electromagnetic waves can travel through vacuum

  • Longitudinal → cannot travel through vacuum

• Medium

  • Transverse → can move in solids and on the surface of liquids, but not inside liquids or gases

  • Longitudinal → can move in solids, liquids, and gases

• Density

  • Transverse → constant density

  • Longitudinal → changing density

• Pressure

  • Transverse → constant pressure

  • Longitudinal → changing pressure

• Wave speed

  • Transverse → dependent on medium

  • Longitudinal → dependent on medium

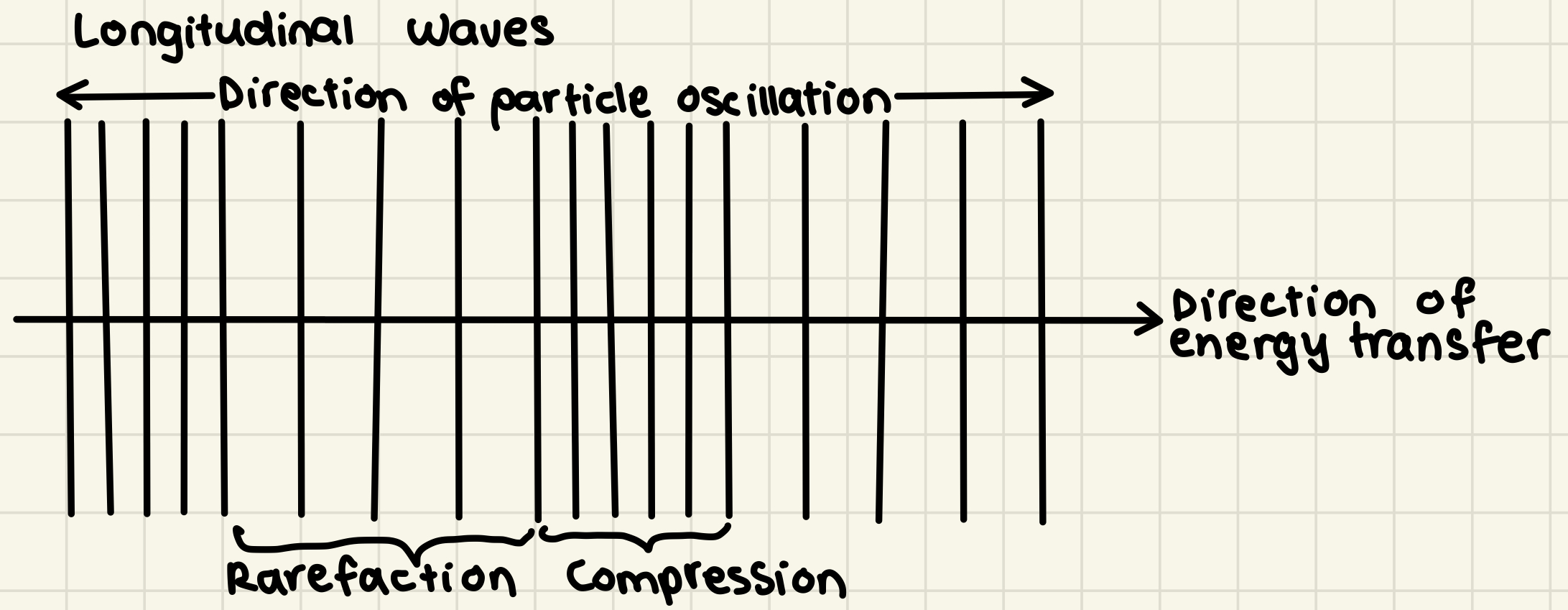
How are longitudinal waves drawn/represented?

Drawn as a set of vertical lines with rarefactions and compressions. Direction of energy transfer as well as direction of particle motion are also drawn with arrows to show these are parallel to one another

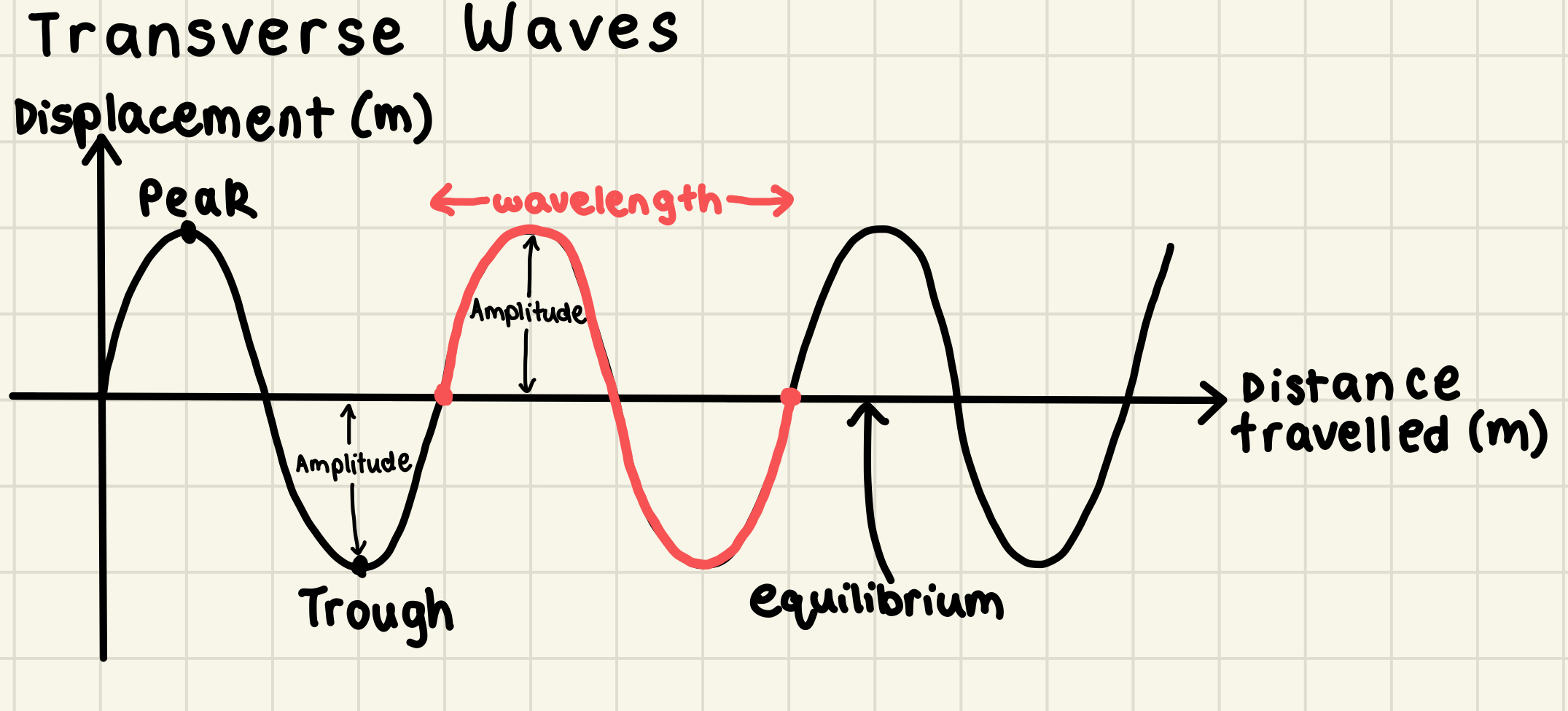
Crest (a.k.a. peak)

Highest point on a transverse wave

Trough

Lowest point on a transverse wave

Equilibrium

a.k.a. “undisturbed position” or “mean position”

Where all forces are balanced and the resultant force is 0

It is the position that the medium the wave is passing through would rest at if no disturbance (i.e. the wave’s energy and forces) were passing through or exerted onto it (e.g. resting position of a string when we are attempting to demonstrate a transverse wave by swinging it vertically up and down, if there were no disturbances moving through it)

Equilibrium is drawn as a horizontal line that is vertically in the middle of the transverse wave

Amplitude

Distance from the undisturbed position (equilibrium) to the crest/peak or trough of a wave

It is the maximum (if crest/peak) or minimum (if trough) displacement from the undisturbed position (equilibrium); amplitude is a vector so can have a positive (crest - equilibrium) or negative (trough - equilibrium) value

Measured in meters (m)

Wavelength

Distance between one point on a wave to the same point on the next wave; it is the length of a complete wave cycle

Measured in meters (m)

Usually represented by the Greek letter lambda or λ

Rarefaction

Region in a longitudinal wave where the particles are furthest apart, usually depicted by drawing the vertical lines farther away from one another

Compression

Region in a longitudinal wave where the particles are closest together, usually depicted by drawing the vertical lines closer to one another

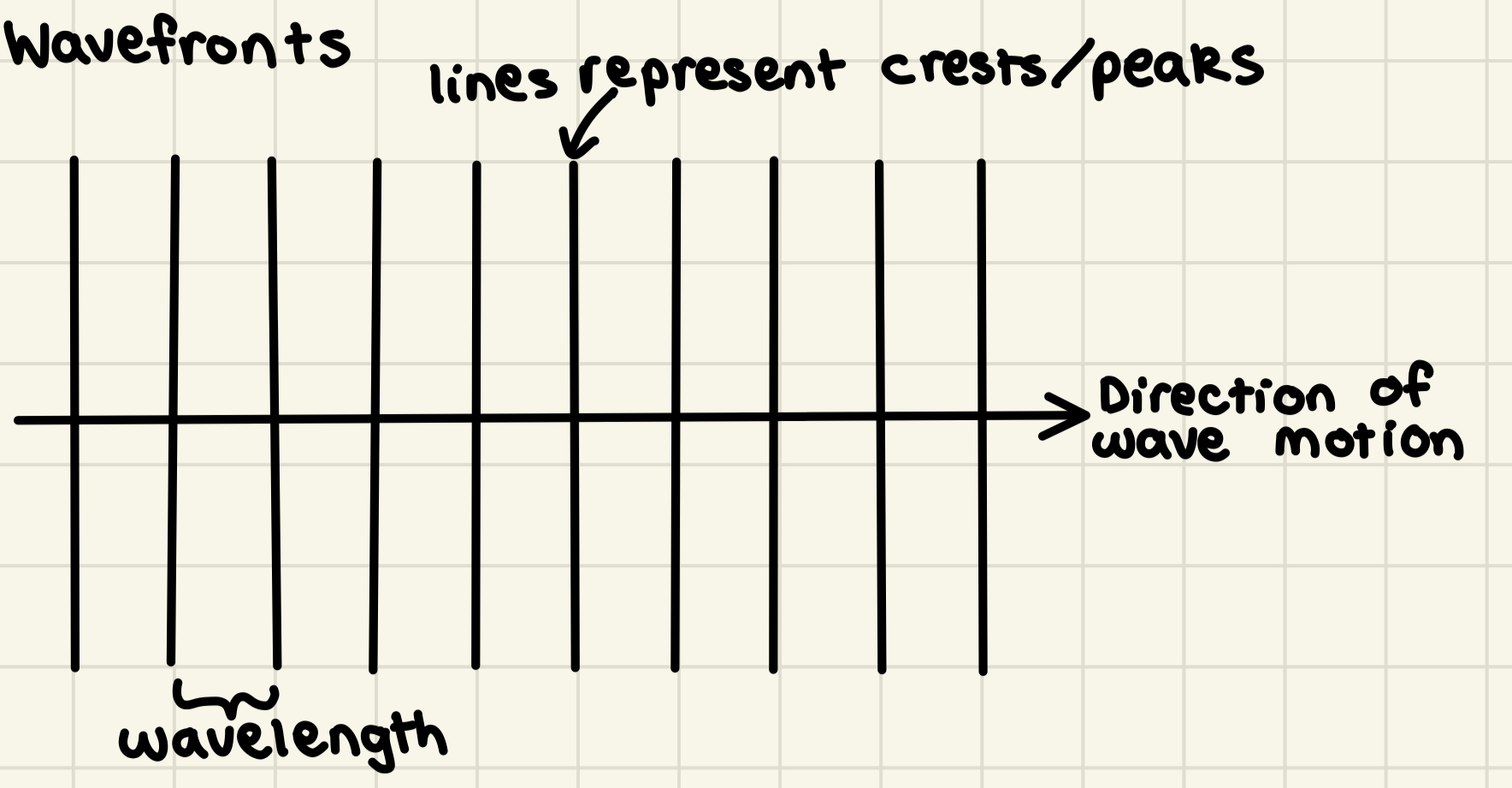
Wavefront

Useful diagrams that depict waves from a top view looking downwards (i.e. the lines we see are drawings of the wave’s crests/peaks)

Each vertical line/wavefront represents a crest/peak

Gaps between lines (i.e. gaps between successive crests/peaks) represent wavelength

• short gap → short wavelength

• long gap → long wavelength

Arrow (sometimes called a ray) depicts direction of wave motion

Frequency

Number of complete waves passing through a point per second

Measured in Hertz (Hz) where 1Hz = 1 complete wave passing through per second

Period (sometimes also called time period)

Time taken to complete 1 full wave cycle/vibration

Time taken for 1 full wave cycle/vibration to pass through a single point

Measured in seconds (s)

Wave speed equation

Wave speed (m/s) = Frequency (Hz) \* Wavelength (m)

v = f \* λ

Relationships (proportionalities) between wave speed, frequency, and wavelength

• frequency ∝ wave speed (for constant wavelength)

  • ↑ frequency → ↑ wave speed

  • ↓ frequency → ↓ wave speed

  • direct proportionality

• wavelength ∝ wave speed (for constant frequency)

  • ↑ wavelength → ↑ wave speed

  • ↓ wavelength → ↓ wave speed

  • direct proportionality

• frequency ∝ 1/wavelength (for constant wave speed)

  • ↑ frequency → ↓ wavelength

  • ↓ frequency → ↑ wavelength

  • inverse proportionality

Frequency equation

Frequency (Hz) = 1 / Time period (s)

f = 1 / T

Relationship (proportionality) between frequency and time period

• ↑ time period → ↓ frequency

• ↓ time period → ↑ frequency

• inverse proportionality

Wave speed in uniform medium

Wave speed stays constant in uniform medium

Even if wavelength changes, if waves are in the same medium, then the wave speed will stay uniform (frequency will decrease instead)