Transformations, Congruence, and Similarity

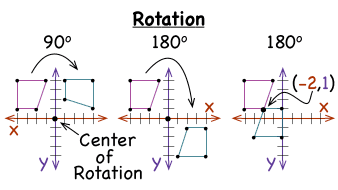
Rotation

Turn

Reflection

Flip or mirror image

Translation

slide

Dilation

enlarge or reduce a shape by multiplying/dividing by a scale factor

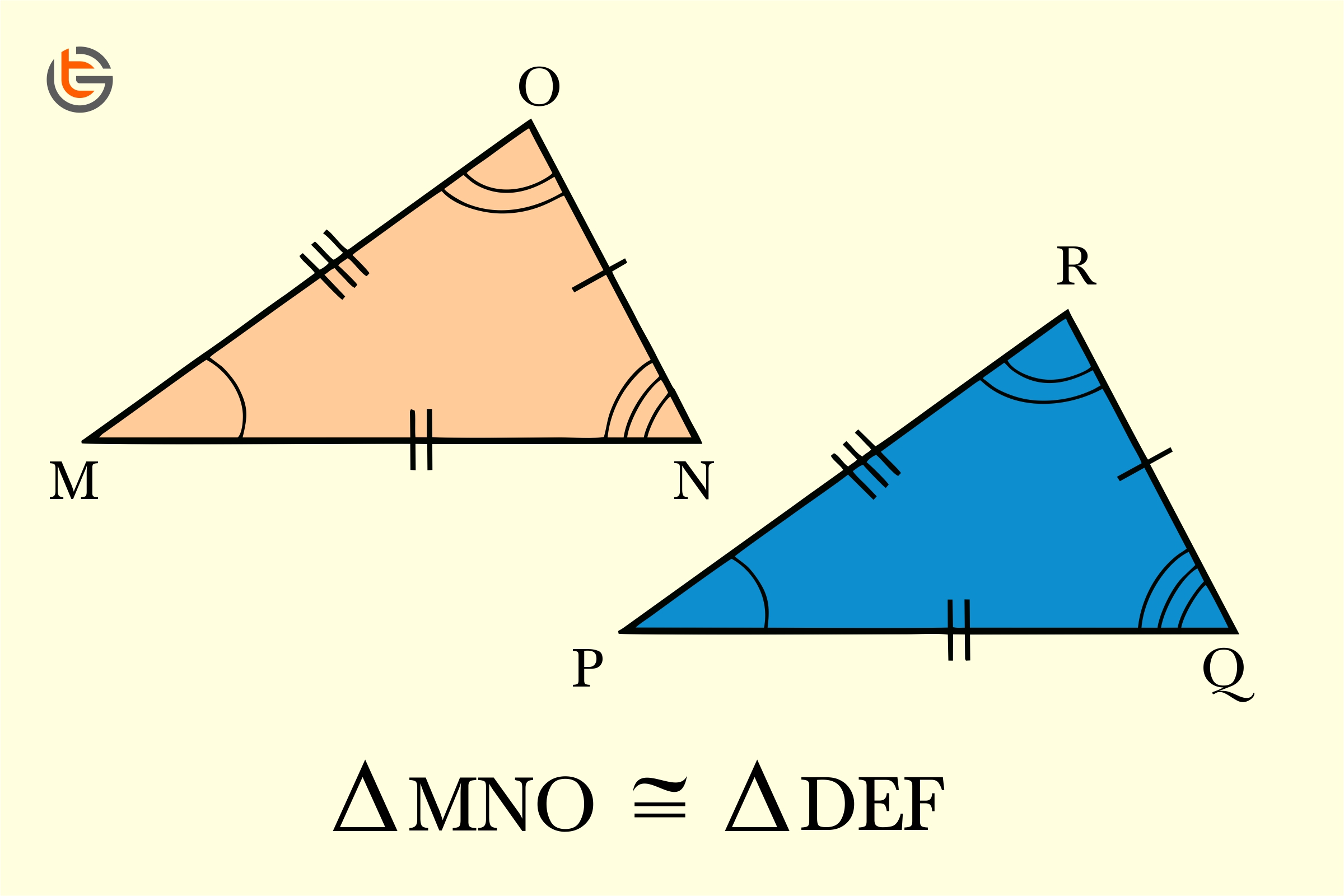
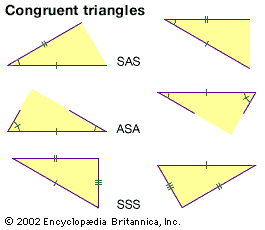
Congruent

shapes that are exactly the same—same shape and same size

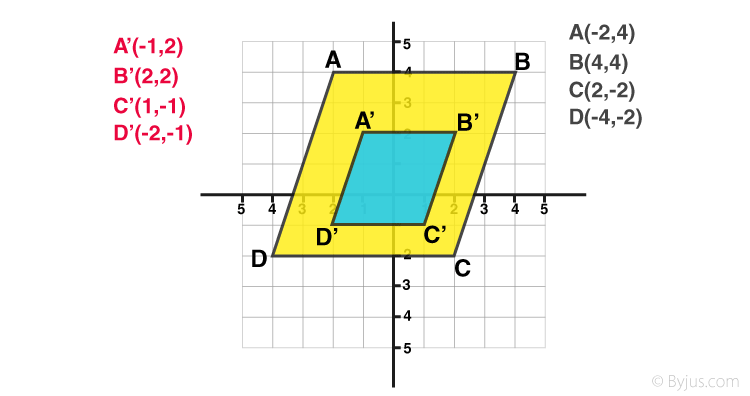
Similar

shapes that have the same shape but different (proportional) size

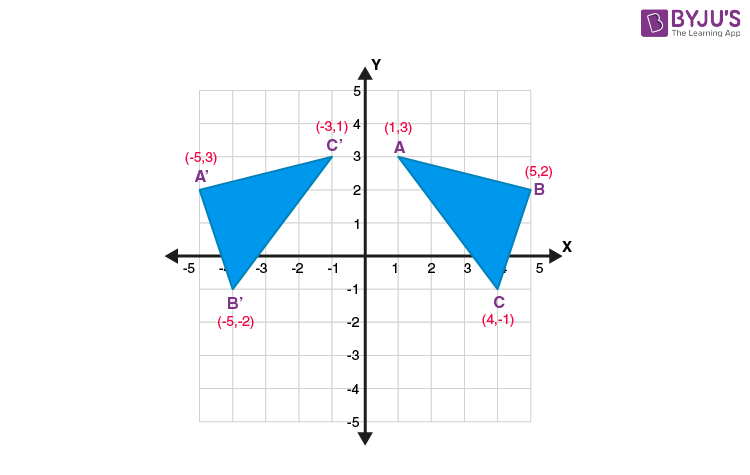
Reflection across the x-axis

Keep x-value the same, take the opposite of new y-value [Example: (3, 2)  (3, -2)]

Reflection across the y-axis

Keep y-value the same, take opposite of new x-value [Example: (3, 2)  (-3, 2)]

Rotation 90o clockwise

Switch coordinates, take opposite of new y-value [Example: (3, 2)  (2, -3)]

Rotation 90o counterclockwise

Switch coordinates, take opposite of new x-value [Example: (3, 2)  (-2, 3)]

Rotation 180

Take opposite of both x-value and y-value [Example: (3, 2)  (-3, -2)]

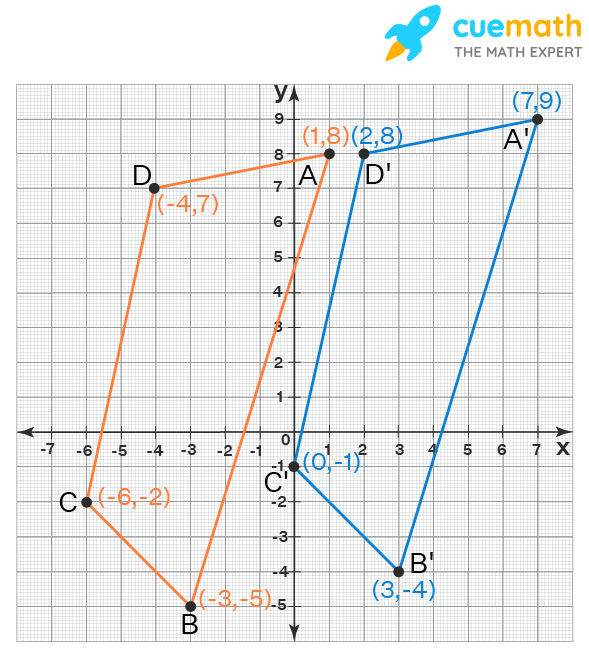
Translations

: If given a rule, use the coordinates given and “plug” them in for the x and y in the second part of the rule [Example: Rule: (x, y)  (x – 10, y + 4), Coordinate given: (3, 2); (3 – 10, 2 + 4) = (-7, 6)] -If given “directions”, remember “left” and “right” affect the x-value. “Up” and “Down” affect the y-value

Dilations

multiply both the x and y values by the scale factor (k) given. [Example: k = 3, coordinate given (3, 2) (9, 6) or k = ½ , coordinate given (3, 2)  (1.5, 1)]

≅

means congruent

~

means similar

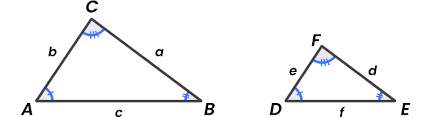
m∠x

means “ measure of angle the x

𝑿𝒀̅̅̅̅

means “line segment” or “side length” from point X to point Y

∥

means “is parallel to”