Geometry Vocabulary

4.5, 4.6, 5.1, 5.2, 5.3, and 5.4

Isosceles Triangle

Triangle with two congruent sides

Equilateral Triangle

Triangle with all congruent sides

Opposite Side

A side located to the opposite direction of a specific angle

Opposite Angle

An angle located to the opposite direction of a specific side

Corollary

A theorem that can be used to prove another theorem

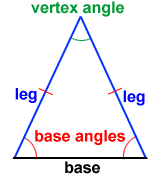
Parts of an Isosceles Triangle

Base

Legs

Vertex Angle

Base Angles

Base

Non-congruent side

Legs

Congruent sides

Vertex Angle

Angle between the 2 legs

Base Angles

Angles between the base and the legs

Isosceles Angle Theorem

If two sides of a triangle are congruent, then the angles opposite to those sides are congruent

Converse of the Isosceles Angle Theorem

If two angles of a triangle are congruent, then the sides opposite to those angles are congruent

Theorem 4.5

If a line bisects the vertex angle of an isosceles triangle, then the line is also a perpendicular bisector to the base

Corollary of Theorem 4.3

If a triangle is equilateral, then the triangle is also equiangular

Corollary of Theorem 4.4

If a triangle is equiangular, then the triangle is also equilateral

Right Triangle

Triangle that has 1 right angle

Hypotenuse

A side located to the opposite direction of the right angle in a right triangle

Legs (Right Triangle)

Sides that are not the hypotenuse

Hypotenuse-Leg Theorem (HL)

If the hypotenuse and the leg of one triangle are congruent to the hypotenuse and a leg of another right triangle, then the triangle are congruent

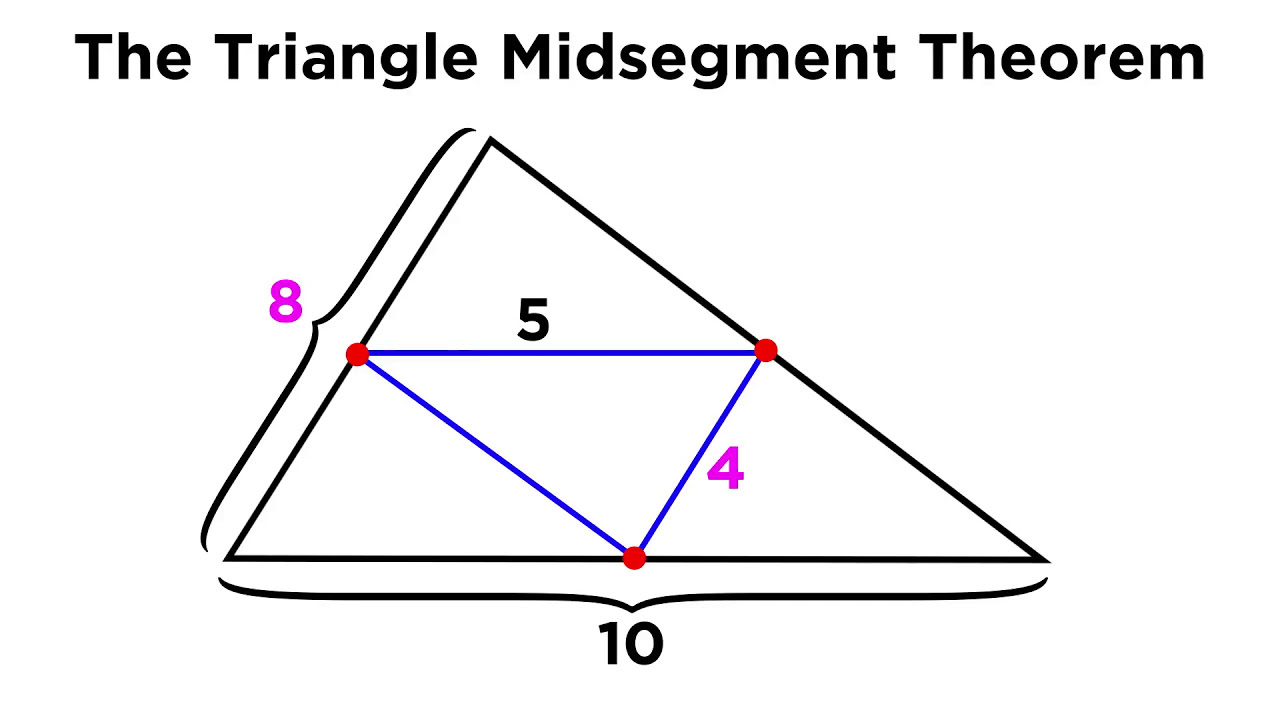
Triangle Midsegment Theorem

If a segment joins the midpoint of two sides of a triangle, the the segment is parallel to the third side, and is half long.

Perpendicular Bisector

Line that cuts another line into 90° angles

Angle Bisector

Line that cuts an angle in half

Equidistant

Something that is at the same distance from 2+ figures

Distance

Perpendicular segment from the point to the line. At the same time, the distance did the shortest segment from said point to said line.

Perpendicular Bisector Theorem

If a point is on the perpendicular bisector of a segment, then it is equidistant from the endpoints of the segments

Converse of the Perpendicular Bisector Theorem

If a point is equidistant from the endpoints of the segments, then it is on the perpendicular bisector of a segment

Angle Bisector Theorem

If a point is on the bisector of an angle, then the point is equidistant from the sides of the angle

Converse of the Angle Bisector Theorem

If the point on the interior of an angle is equidistant from the sides of the angle, then the point is on the bisector of an angle

Concurrency

When 3+ lines intersect at one point. The point where they intersect is the point of concurrency.

Concurrency of Perpendicular Bisectors Theorem

The perpendicular bisectors of the sides of a triangle are concurrent at a point equidistant to the vertices

Circumscribed

Point of concurrency of the perpendicular bisector of a triangle. If you trace a circle around the vertices of a triangle, the point of concurrency is also the center of said circle.

Concurrency of Angle Bisectors Theorem

The angle bisectors of a triangle are concurrent at a point equidistant to the sides of the triangle

Inscribed

The point of concurrency of the angle bisectors of a triangle is called the incenter. This is because if you trace a circle that touches all the sides of the triangle, the point of concurrency is the center of said circle.

Median of a Triangle

Segment whose endpoints are the vertex and the midpoint of the opposite side of a triangle

Centroid of a Triangle

Point of concurrency of the medians of a triangle (always inside)

Concurrency of Medians Theorem

The medians of a triangle are concurrent at a point (centroid) that is at the 2/3 the distance between the vertex and the midpoint of the opposite side

Altitude of a Triangle

A perpendicular segment from a vertex of a triangle to a line contained in the opposite side. It can be inside, on or outside the triangle

Orthocenter of a Triangle

The point of concurrency of the altitudes of a triangle. Inside, outside or on the triangle

Concurrency of Altitudes Theorem

The lines that contain the altitudes of a triangle are concurrent at an orthocenter