Chapter 8: Rotation II: Inertia, Equilibrium, and Combined Rotation/Translation

Solution

________ ● The minimum coefficient of friction occurs when the object is on the verge of slipping.

Angular momentum

________ is conserved if the external torque is zero.

gravitational force

○ The torque exerted by gravity acts as if the ________ is exerted at the center of mass.

● Tip

________: Once you know the rotational inertia for an axis through the CM, you can use this theorem to find I through a parallel axis.

Linear momentum

________ is conserved if the external force is zero.

axis of rotation

B) The mass density is given to you as a function of the distance from the ________.

Your choice of differential region will be guided by the requirement that every particle of mass in

side the differential region must share a common distance to the axis of rotation

\

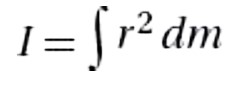
**Definition of rotational inertia**

There are two situations concerning these mass densities that you should be able to handle

a) The mass density is uniform

8.2

Parallel Axis Theorem ● The rotational inertia of an object about an axis a distance D from its center of mass (Iparallel axis) is related to the rotational inertia of the object about a parallel axis running through its center of mass (ICM) according to the equation

● Tip

Once you know the rotational inertia for an axis through the CM, you can use this theorem to find I through a parallel axis

8.3

Angular Momentum ● Definition of angular momentum for a point particle

Example 8.3.1 Problem

A person is sitting on a rotating lab stool holding a top that is free to rotate, as shown in Figure

8.4

Rolling Without Slipping Relating Linear and Angular Coordinates for the Center of Mass of an Object that Rolls Without Slipping ● Imagine a spool of thread of radius R that rolls along a surface without slipping, laying down thread ● The translational velocity of the center of mass equals the rate at which thread is laid down, dl/dt

Problem

A cylinder ( ) is at rest on a flat surface

● Now, for the object to roll without slipping, the equation 𝑎 = 𝑅α must be satisfied

𝑐𝑒𝑛𝑡𝑒𝑟

Satisfying 𝐹 = 0

Choose a convenient coordinate system, and sketch all forces acting𝑛𝑒𝑡 on the object

Satisfying τ = 0

The following statements are equivalent if the net force is zero

○ Proof

Consider the torque exerted by gravity about the z-axis on an arbitrary mass distributed along an xy-plane

○ Selection of axis

If we choose the axis to pass through the point where the ladder contacts the ground, the torque due to FN and Ffr will be zero, giving us a simple equation

This is straightforward because of our choice of axis

The last equation can be immediately solved for F′N, which can then be plugged into the first equation to calculate Ffr

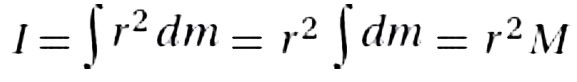
**Rotational inertia** for point masses, rings, and cylindrical shells rotating about their axes

**line segments**

One-dimensional mass ⇒ differential **_________**

**rings**

Two-dimensional mass rotating about an axis perpendicular to its plane ⇒ **_________**

**rectangular strips**

Two-dimensional mass rotating about an axis contained in its plane ⇒ **___________**

**cylindrical shells**

Three-dimensional mass ⇒ **_________** whose axes lies along the axis of rotation

2πr dr

**Area of a ring**

(2πr dr)h

**Volume of a cylindrical shell**

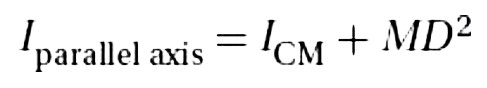
**Parallel Axis Theorem**

L = r x p

Definition of **angular momentum for a point particle**

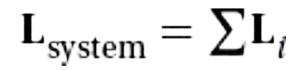
Net angular momentum of a system of particles

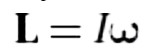
Relationship between angular momentum and angular inertia for an extended object rotating about a symmetry axis

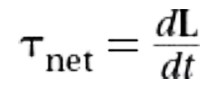
Relationship between net torque and angular momentum

Angular momentum

It is conserved if the external torque is zero.

Linear momentum

It is conserved if the external force is zero.

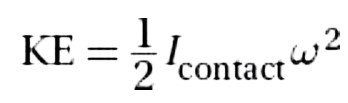
***Object’s Kinetic Energy***

**Equilibrium**

A system that is not accelerating

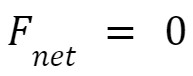
For a point mass, equilibrium is defined by the requirement that __________

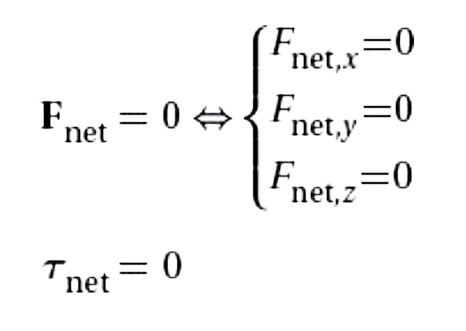
Conditions required for equilibrium