One continuous variable

ONE CONTINUOUS VARIABLE

What does a one-sample t-test evaluate? (t.test() or oneSampleTTest())

Formal name: Student’s t-test

It tests whether the mean of a sample differs significantly from a known or hypothesized population mean.

• H₀: population mean equals a specific value

• H₁: population mean does not equal a specific value

*If the population standard deviation is known: t-test becomes z-test

What is the t-test statistic, and how are degrees of freedom calculated?

• xˉ = sample mean

• μ0 = hypothesized population mean

• s = sample standard deviation

• n = sample size

Degrees of freedom: df = N − 1

• N is the number of observations in the dataset

*exact rejection regions depend on degrees of freedom

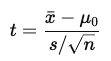
What is Cohen’s d and how is it interpreted?  (cohensD()) - Effect size

Cohen’s d measures the magnitude of difference between the sample mean and the population mean:

• 0.20 = small effect

• 0.50 = medium effect

• 0.80 = large effect

*larger values correspond to a greater difference from the value under H0

What are the 2 assumptions of a one-sample t-test?

• The continuous variable is normally distributed (check with Shapiro-Wilk test, histogram, Q-Q plot)

  • if normality is violated: use the Wilcoxon signed-rank test (wilcox.test())

• Observations are independent

What are key properties of the t-distribution used in t-tests?

• The t-distribution has thicker tails than the normal distribution (to account for extra uncertainty in small samples)

• As sample size increases, the t-distribution approaches the normal distribution

• Larger absolute t-values indicate more extreme results, corresponding to a lower probability of H₀ being true