psychology 2910 - lecture 8 (percentiles)

Is the 90th percentile better or worse than the 30th percentile?

The 90th percentile is always better than the 30th percentile

- 90th: 90% of scores are at or below this point; only 10% are higher

- 30th: 30% of scores are at or below this point; 70% are higher

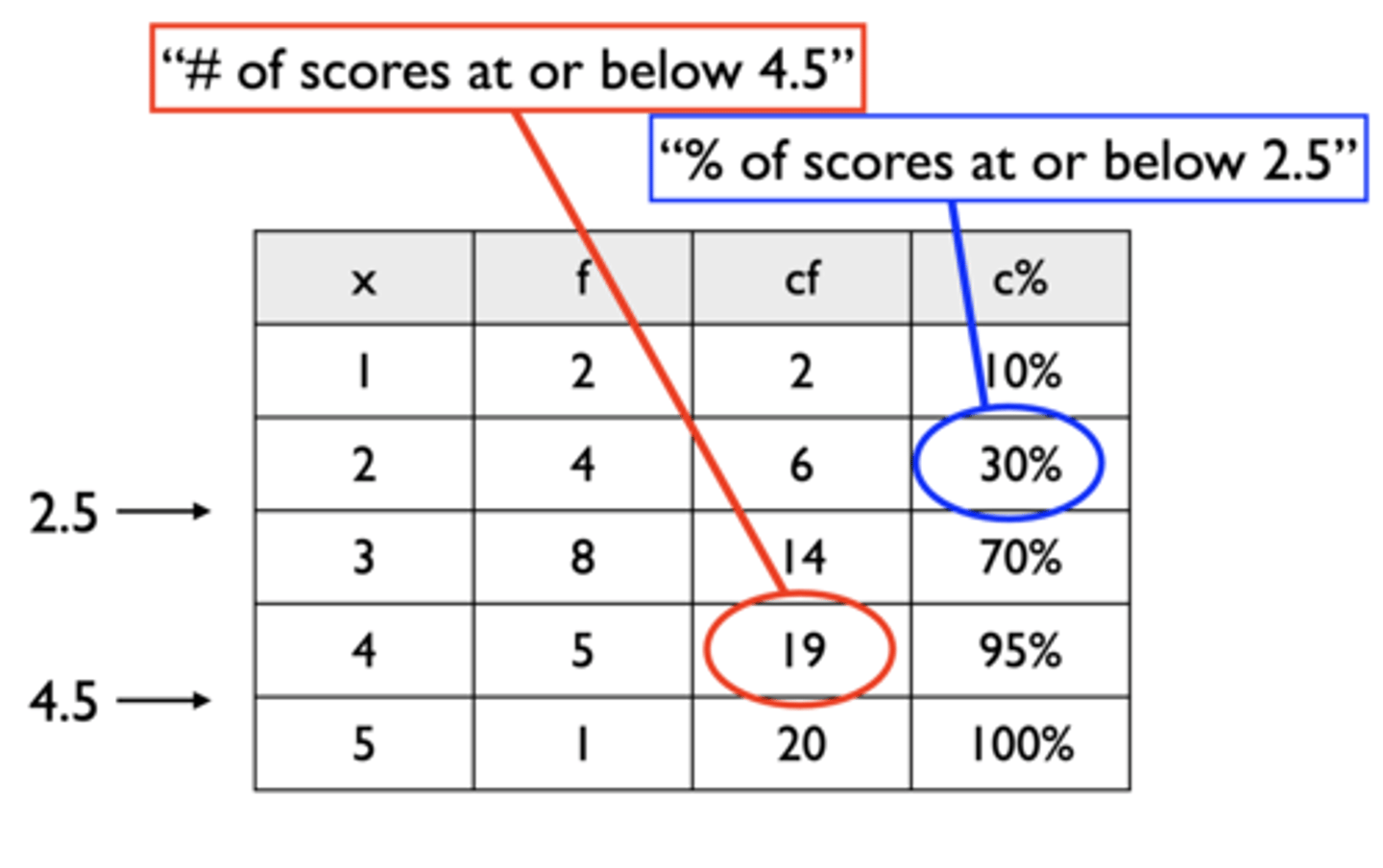
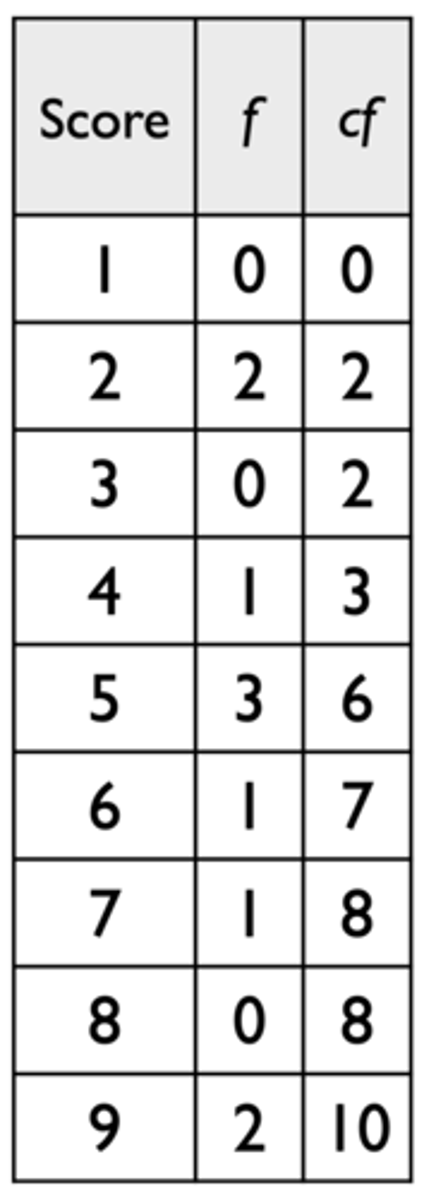
How do we derive percentiles from a frequency table?

30th percentile is at 2.5 or below; 95th percentile is at 4.5 or below

Real Limits

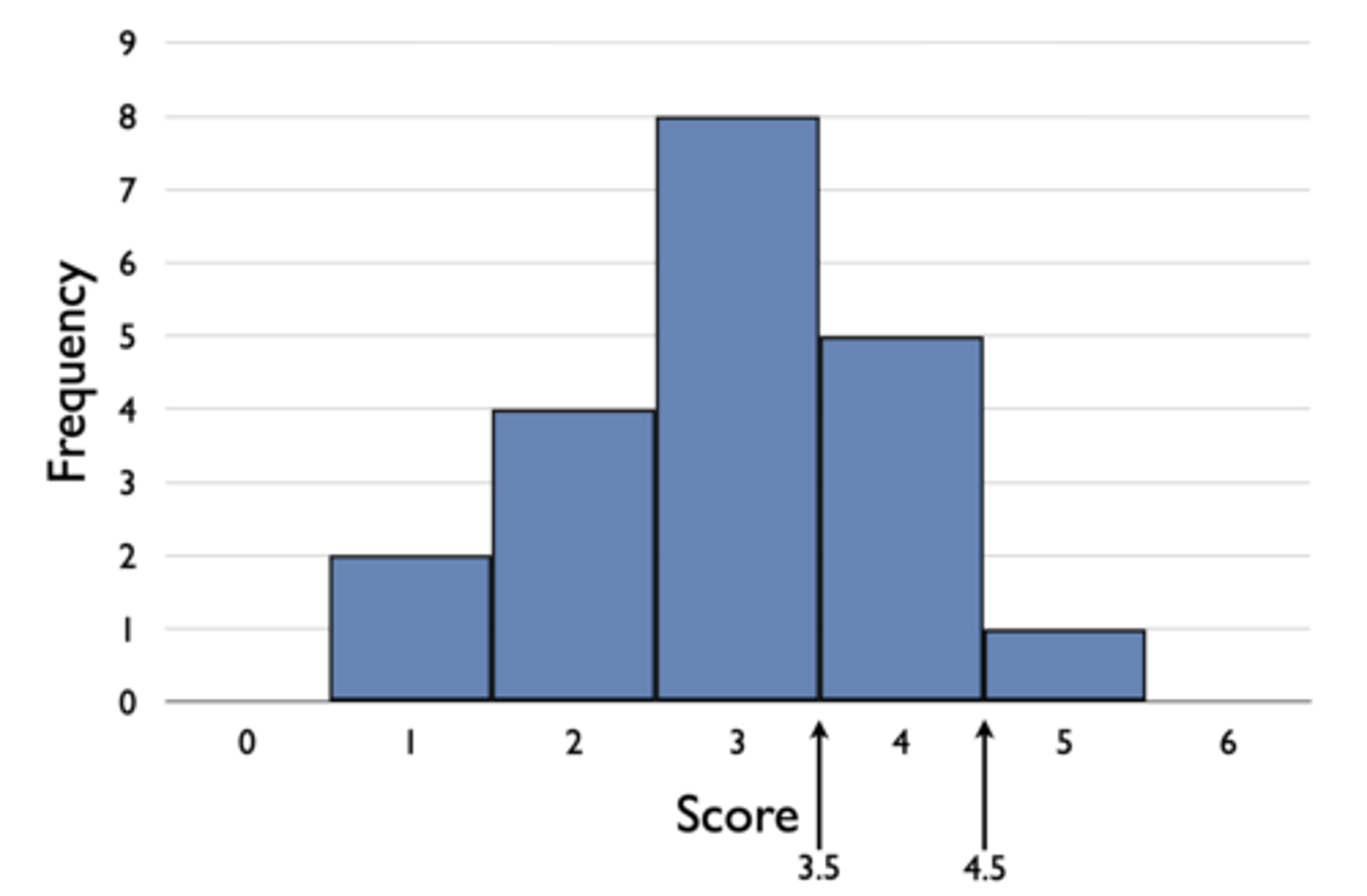
Scores are usually measurements of a continuous variable, but measurement is usually discrete; therefore, need to consider upper and lower real limits

- Scores from 2.5 to 3.5 measured as 3

- Scores from 3.5 to 4.5 measured as 4

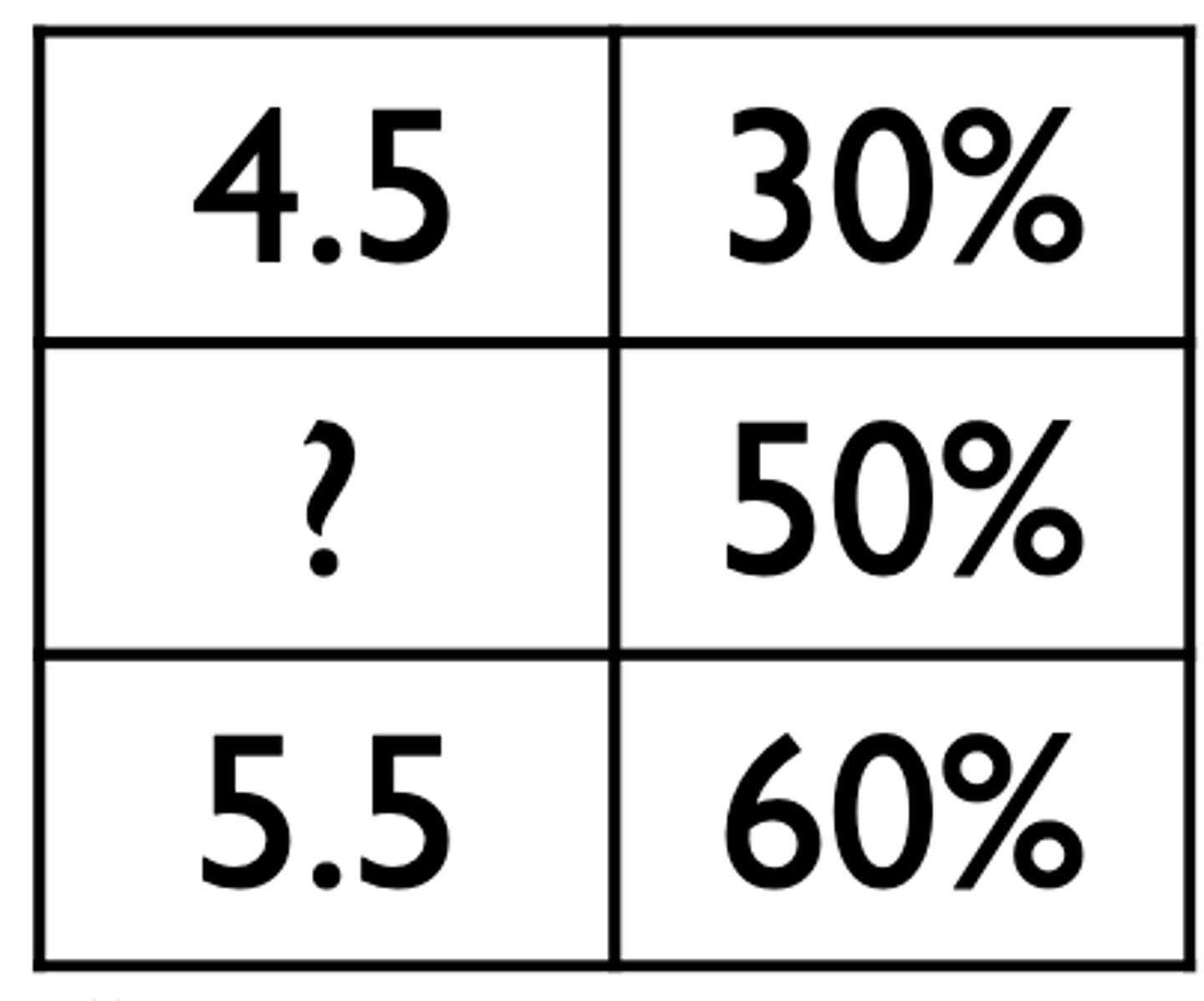
When the 50th percentile isn't specified, what two methods can we use to calculate it?

1. Interpolation

- Find the value that corresponds to 50th percentile

- Find the percentile that corresponds to a score

2. Formula

- Find the value that corresponds to 50th percentile

- Find the percentile that corresponds to a score

- You get the same answer!

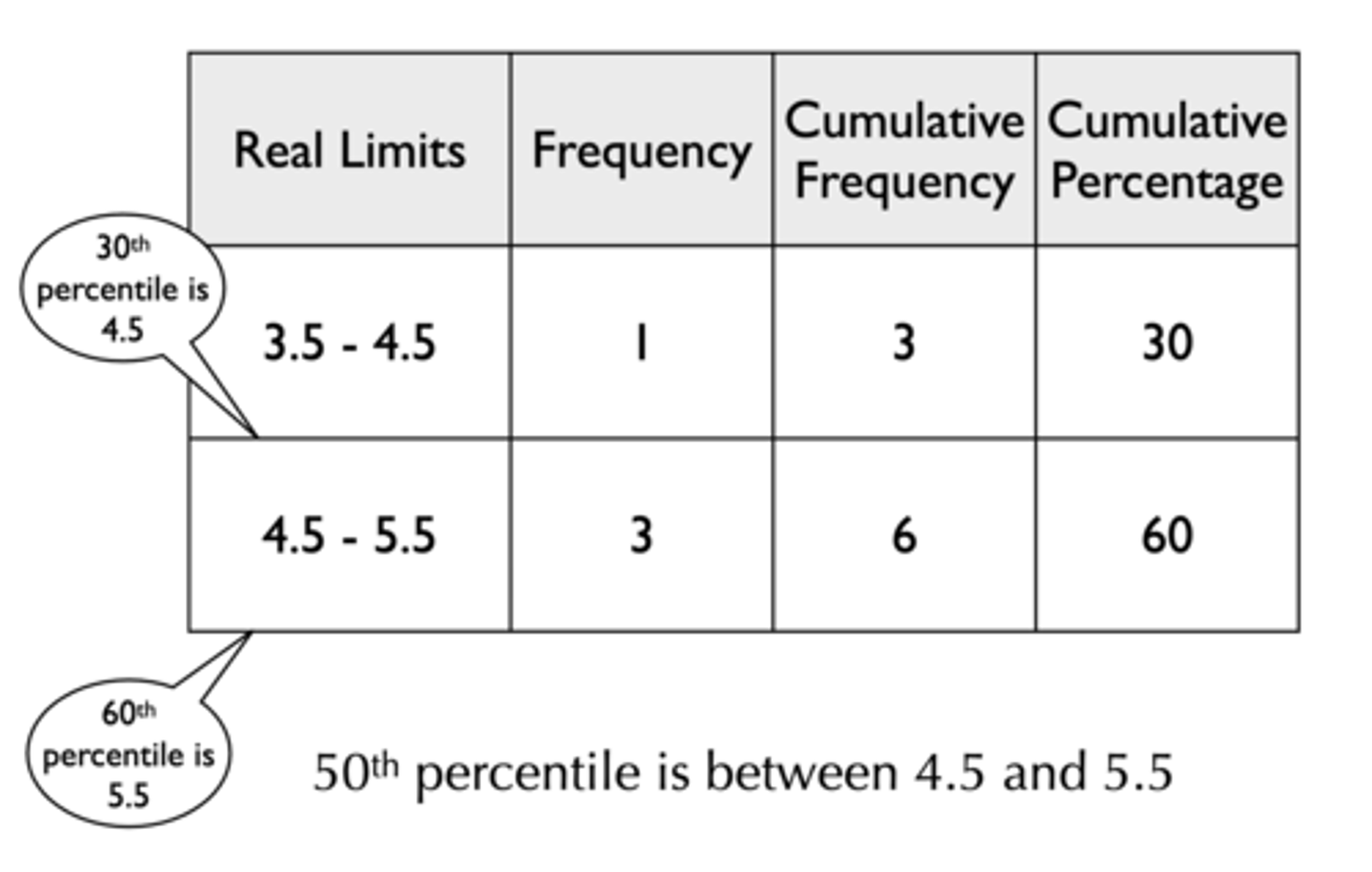
How can you calculate the 50th percentile using interpolation?

Step 1: Determine width of interval

- Width = 5.5 - 4.5 = 1

Step 2: Determine distance to go

- Where is 50% relative to 30% and 60%? (e.g. 45% is halfway)

- Distance between 50% and 30% is 20%

- Distance between 60% and 30% is 30%

- 20% / 30% = 2/3

Step 3: Determine 2/3 of distance between 4.5 and 5.5

- 4.5 + (2/3 x 1) = 5.167

- 4.5 plus (two-thirds times the interval size)

- 50th percentile = 5.167 (50% of scores at or below 5.167)

How can you calculate the 50th percentile using the precise median formula?

- Determine the real limits of interval containing the median: 4.5 to 5.5

- Total number of scores: 10

- Number of scores below: 3

- Number of scores in interval: 3

- Precise median will also be 5.167!

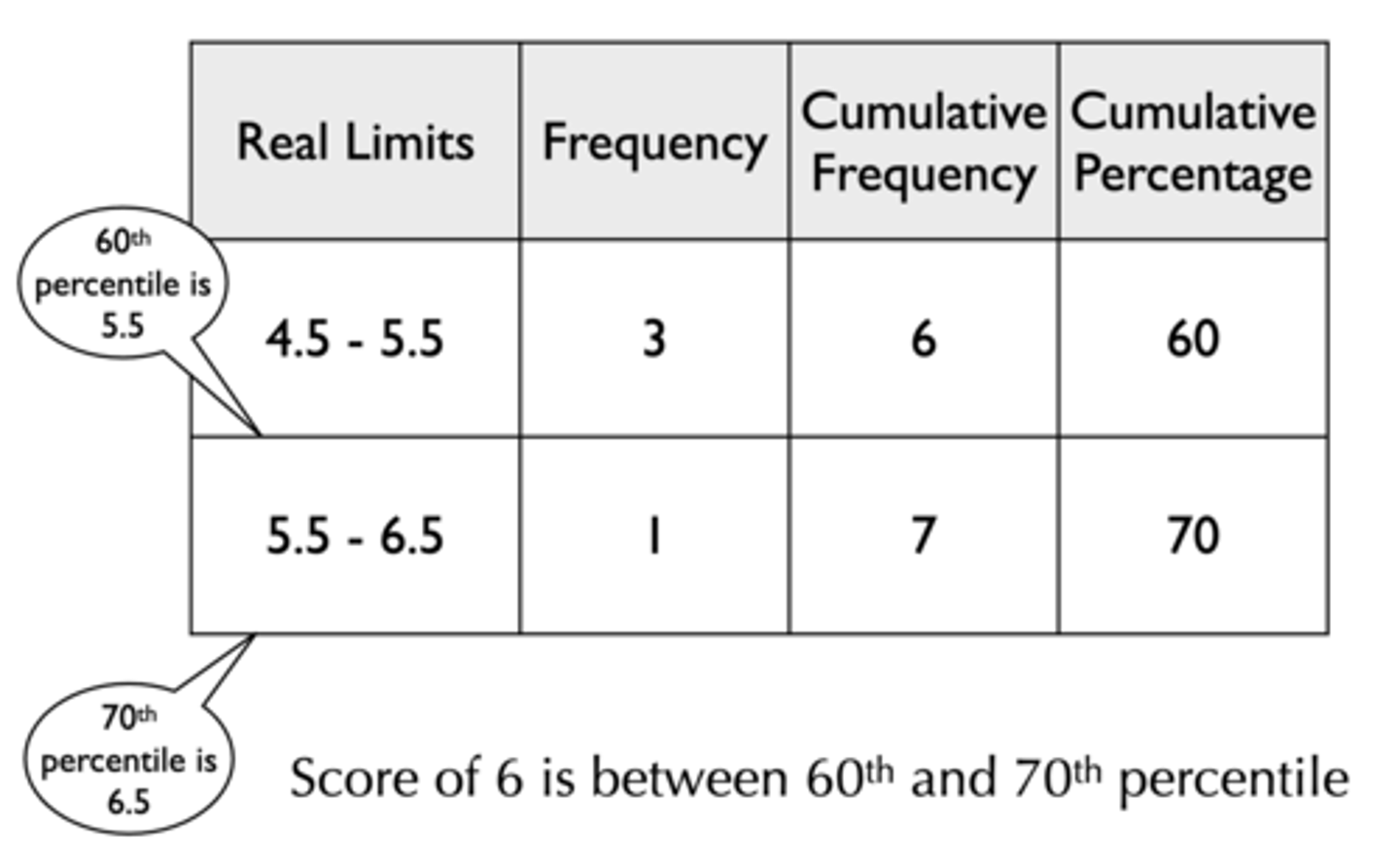
How do you calculate the percentile for a score using interpolation?

Step 1: Determine width of interval

- 70% - 60% = 10%

Step 2: Determine distance to go

- Where is 6 relative to 5.5 and 6.5?

- Distance between 6 and 5.5 is 0.5

- Distance between 6.5 and 5.5 is 1

- 0.5 / 1 = 0.5

Step 3: Determine 1/2 of distance between 60% and 70%

- 60% + (1/2 x 10%) = 65%

- A score of 6 corresponds to the 65th percentile

Interquartile Range

Interquartile Range = Q3 - Q1

- Range covered by middle 50%

- Q3 = 75th percentile

- Q2 = 50th percentile or median

- Q1 = 25th percentile

How can you calculate the percentile for a score of 6 using the percentile formula?

Score for which percentile rank is sought (x) = 6

cf = 6

ll = 5.5

w = 1

f of interval = 1

n = 10

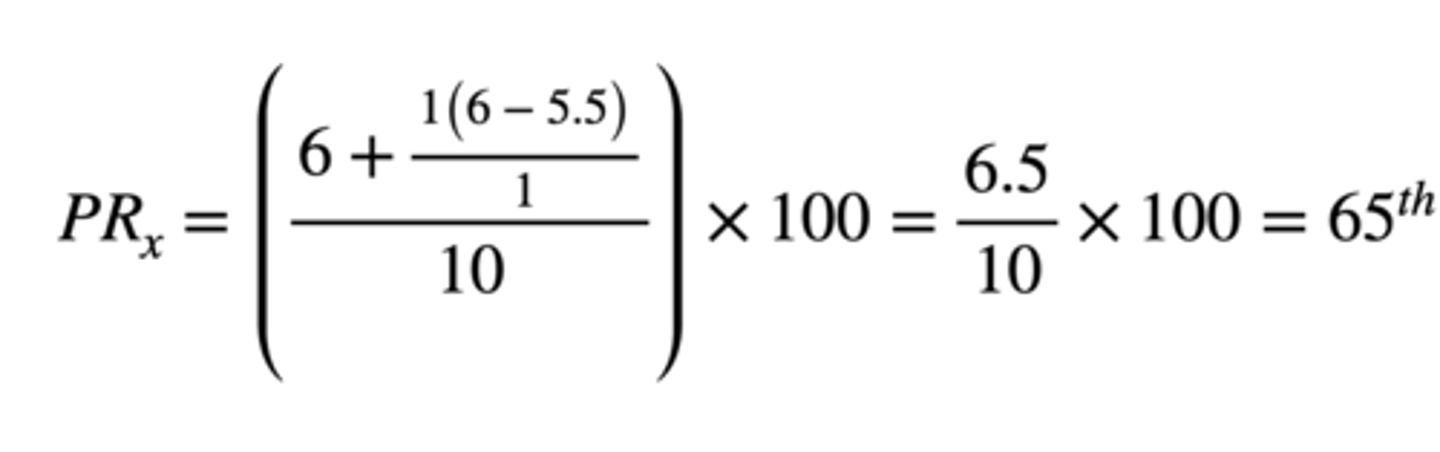
What score corresponds to the 50th percentile (using the percentile formula)?

Percentile rank of x = 50

cf = 2

ll = 4.5

w = 5

f of interval = 10

n = 20

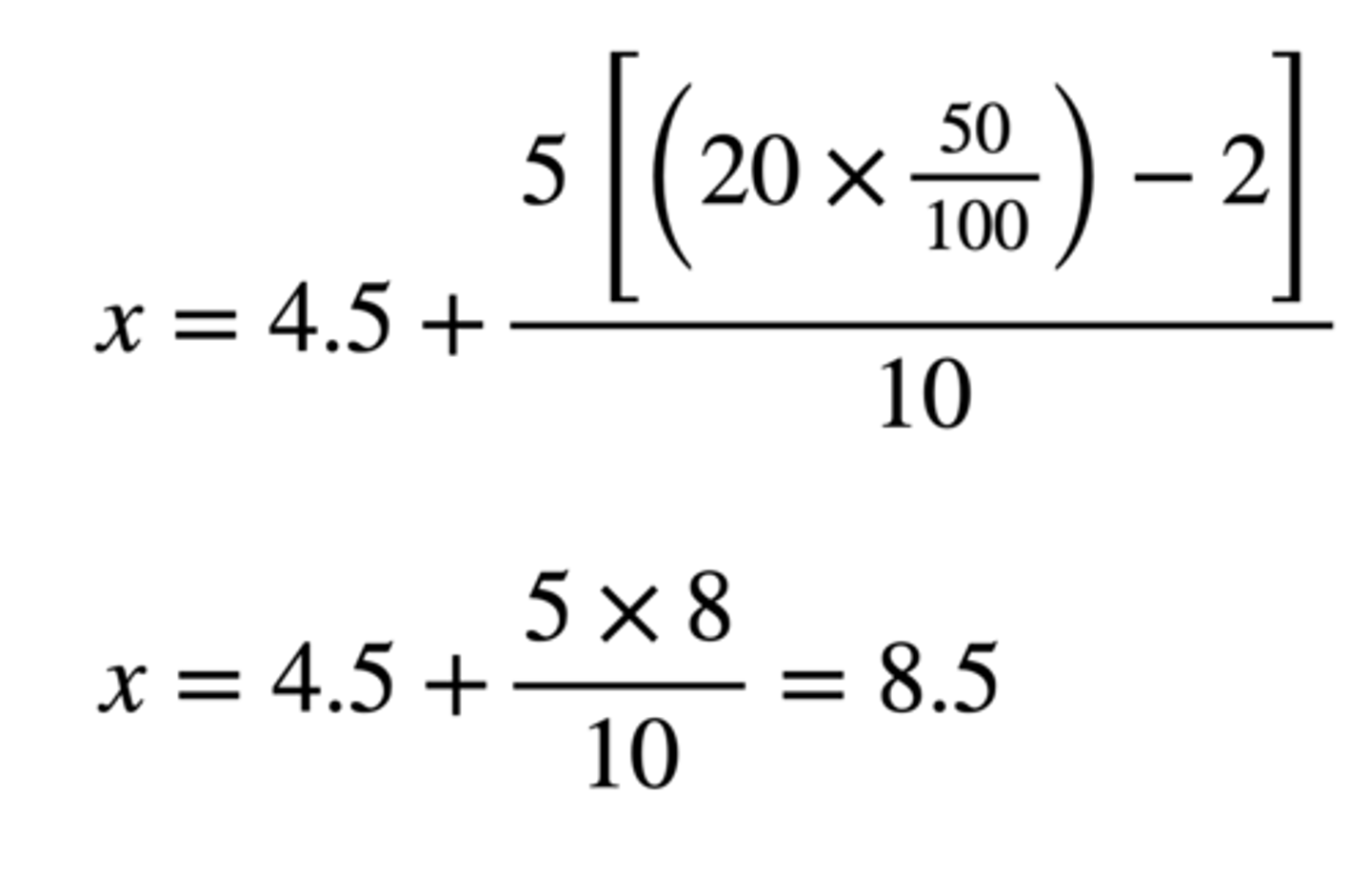
When calculating the precise median from frequency tables, how can you get different answers?

Depends on interval width

- Larger interval width = less precision (because there is less info)

- Smaller interval width = more precision (because there is more info)

- Precise median from 64 alone = 64

- Precise median from 60-69 = 60.125

- Precise median from 60-79 = 59.86