Barron's AP Calc AB+BC Flashcards (Units 1 - 5)

Deck Includes: - Key Formulae - Basic Derivatives + Rules for taking Derivatives - Basic Integrals + Rules for taking Anti-Derivatives (more will be added as I progress through the book)

Unit 1: Functions

Precalc Review of Properties of:

• Rational Functions

• Trig/Inverse Trig Functions

• Exponential/Logarithmic Functions

• Parametric Functions (BC)

• Polar Curves (BC)

Even Function

$f(-x) = -f(x)$

Odd Function

$f(-x) = f(x)$

Rational Function

$f(x) = \frac{p(x)}{q(x)}$
(Domain: set of all real # where $q(x) \neq 0$ )
(Range: $(-\infty, +\infty)$ )

State the Domain and Range for all Trig Functions

State the Domain and Range for all Inverse Trig Functions

Exponential Functions

f(x) = a^x (a>0, a\neq 1)

Logarithmic Function

$y=\log_ax$ IF AND ONLY IF $a^y=x$

Write down all the log properties you remember

• $$\log_a1=0$$

• $$\log_aa=1$$

• $$log_a a^m = m$$

• $\log_amn=\log_am+\log_an$ (Product Rule)

• $\log_a\frac{m}{n} = \log_am-\log_an$ (Quotient Rule)

• $\log_ax^m=m\log_ax$ (Exponent Rule)

• $\log_mn=\frac{\log_an}{\log_am}$ (Change of Base Rule)

Parametric Equation

$x=f(t), y=g(t)$ where $t$ is the parameter

Polar Function

$r=f(\theta)$
(very broad def.)

Write down all the types of polar functions you remember (BC)

• Spiral: $r=\theta$

• Rose Curve: $r= k \cdot sin(m \cdot \theta)$ or $r = k \cdot cos(m \cdot \theta)$

• Limacons: $r= k + m \cdot sin(\theta)$ or $r= k + m \cdot cos (\theta)$ -

  • Dimpled Limacons: k>m

  • Cardioid: $k=m$

  • Limacon w/Inner Loop: k<m

Unit 2: Limits and Continuity

• general properties of limits

• how to find limits

• horizontal and vertical asymptotes

• continuity

• types of discontinuities (removable, jump, infinite)

• Squeeze Theorem

• Extreme Value Theorem

• Intermediate Value Theorem

Limit and One-Sided Limit

• $$\lim_{x \to c} f(x) = L$$

  (as $x$ approaches $c$, $f(x) = L$ )

• $\lim_{x \to c^+} f(x) = L$ or $\lim_{x \to c^-} f(x) = L$

  (as $x$ approaches $c$ from the left or right, $f(x)=L$ )

Horizontal Asymptote and Vertical Asymptote

• $$\lim_{x \to \pm \infty}f(x)=b$$

  (horizontal asymptote)

• $\lim_{x \to a}f(x)=\pm \infty$ OR $\lim_{x \to a^ \pm} f(x) = \pm \infty$

  (vertical asymptote)

Write down all the properties of limits you remember

if $\lim f(x)$ and $\lim g(x)$ are finite numbers (not going to $\pm \infty$ ), then

• $$\lim k \cdot f(x) = k \cdot \lim f(x)$$

• $$\lim [f(x) + g(x)] = \lim f(x) \cdot \lim g(x)$$

• $$\lim (f(x) \cdot g(x)) = \lim f(x) \cdot \lim g(x)$$

• $$\lim {\frac {f(x)}{g(x)}} = \frac{\lim f(x)}{\lim g(x)}$$

• $$\lim_{x \to k} = k$$

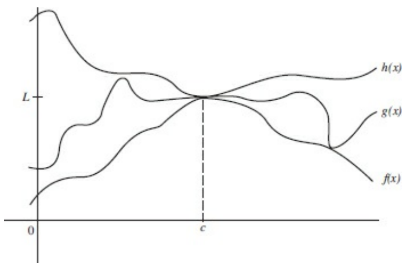
Sandwich (Squeeze) Theorem

if $f(x) \ge g(x) \ge h(x)$ AND
if $\lim_{x \to c} = \lim_{x \to c}=L$,
then $lim_{x \to c} = L$

Rational Function Theorem

• if the degree of p(x) < q(x), then $\lim_{x \to \pm \infty} \frac{p(x)}{q(x)}= 0$
  (horizontal asymptote)

• if the degree of $p(x) = q(x)$, then $\lim_{x \to \pm \infty} \frac{p(x)}{q(x)}= \frac{a_p}{b_q}$ , where a and b are the coefficients of the highest powers
  (horizontal asymptote)

• if the degree of p(x) > q(x), then $\lim_{x \to \pm \infty} \frac{p(x)}{q(x)}= \pm \infty$ (vertical asymptote/DNE)

What is the limit of $sin \theta$?

$\lim_{x \to \theta} \frac {sin \theta}{\theta} = 1$
(if $\theta$ is in rads)

Continuous

• $f(a)$ exists

• $\lim_{x \to a} f(x)$ exists

• $$\lim_{x \to a} f(x) = f(a)$$

Define the three types of discontinuities

• Removable Discontinuity: $\lim_{x \to a} f(x)$ AND $f(a)$ exists, but $\lim_{x \to a} f(x) \ne f(a)$

• Jump Discontinuity: $\lim_{x \to a^+} f(x) \ne \lim_{x \to a^-} f(x)$

• Infinite Discontinuity: $\lim_{x \to a^-} f(x) = \pm \infty$

Extreme Value Theorem

if $f$ is continuous in $[a, b]$, then $f$ has a min and max value in that interval

Intermediate Value Theorem

if $f$ is continuous in $[a, b]$, and $f(a) \le m \le f(b)$, then there is at least one number $d$ in $[a, b]$ that $f(d) = m$

• if $f(a)$ and $f(b)$ have opposite signs then there is a value $d$ in $[a, b]$ where $f(d) = 0$.

Continuous Function Theorem

if $f(x)$ and $g(x)$ are both continuous at $x=c$, the following will also be continuous:

• $$k \cdot f(x)$$

• $$f(x) \pm g(x)$$

• $$f(x) \cdot g(x)$$

• $\frac{f(x)}{g(x)}$, if $g(x) \neq 0$

Unit 3: Differentiation

• definitions of derivatives

• estimating derivatives

• derivatives of basic functions

• product, quotient, chain rules

• implicit differentiation

• Rolle’s Theorem

• Mean Value Theorem

• L’Hopital’s Rule

• derivatives of parametric functions (BC)

Derivative

• $\lim_{\Delta x \to 0} \frac{f(x+\Delta x)-f(x)}{\Delta x}$, often notated as $f’(x), y’, \frac{dy}{dx}$, or $D_xy$

Difference Quotient

• $$\frac{f(a+h)-f(a)}{h}$$

• Represents the avg. rate of change from $a$ to $a+h$.

Symmetric Difference Quotient

$$f’(a) \simeq \frac{f(a+h)-f(a-h)}{2h}$$

Derivatives of Constants and Coefficients

($a$ and $n$ are constants and $u$ and $v$ are differentiable functions of $x$)

• $$\frac{da}{dx}=0$$

• $$\frac{d}{dx}au=a\frac{du}{dx}$$

Chain Rule

$$\frac{dy}{du} \cdot \frac{du}{dx}$$

“Take the derivative of the “outside” function w/the “inside” function left the same, then multiply by the derivative of the “inside” one”

^^very important concept, make sure you understand!

Power Rule

($a$ and $n$ are constants and $u$ and $v$ are differentiable functions of $x$)

• $$\frac{d}{dx}u^a=au^{a-1}\frac{du}{dx}$$

Addition and Subtraction Rules

($a$ and $n$ are constants and $u$ and $v$ are differentiable functions of $x$)

• $$\frac{d}{dx}(u+v)=\frac{d}{dx}u+\frac{d}{dx}v$$

• $$\frac{d}{dx}(u-v)=\frac{d}{dx}u-\frac{d}{dx}v$$

Product Rule

($a$ and $n$ are constants and $u$ and $v$ are differentiable functions of $x$)

$$\frac{d}{dx}(u \cdot v)=u \frac{dv}{dx}+v \frac{du}{dx}$$

Quotient Rule

$$\frac{d}{dx}(\frac{u}{v})=\frac{{v \frac{du}{dx}}-u \frac{du}{dx}}{v²}, (v \neq 0)$$

Sine and Cosine Derivatives

($a$ and $n$ are constants and $u$ and $v$ are differentiable functions of $x$)

• $$\frac{d}{dx} \sin u = \cos u \frac{d}{dx}$$

• $$\frac{d}{dx} \cos u = -\sin u \frac{d}{dx}$$

Tangent and Cotangent Derivatives

($a$ and $n$ are constants and $u$ and $v$ are differentiable functions of $x$)

• $$\frac{d}{dx} \tan u = \sec²u \frac{du}{dx}$$

• $$\frac{d}{dx} \cot u = -\csc²u \frac{du}{dx}$$

Secant and Cosecant Derivatives

($a$ and $n$ are constants and $u$ and $v$ are differentiable functions of $x$)

• $$\frac{d}{dx} \sec u = \sec u \tan u \frac{du}{dx}$$

• $$\frac{d}{dx} \csc u = -\csc u \cot u \frac{du}{dx}$$

Exponent and Natural Log Derivatives

($a$ and $n$ are constants and $u$ and $v$ are differentiable functions of $x$)

• $$\frac{d}{dx}a^u = a^u \ln a \frac{du}{dx}$$

• $$\frac{d}{dx} e^u = e^u \frac{du}{dx}$$

• $$\frac{d}{dx} \ln u = \frac{1}{u} \cdot \frac{du}{dx}$$

Arcsin and Arccos Derivatives

($a$ and $n$ are constants and $u$ and $v$ are differentiable functions of $x$)

• \frac{d}{dx} \sin^{-1}u = \frac{1}{\sqrt{1-u²}} \cdot \frac{du}{dx}, (-1<u<1)

• \frac{d}{dx} \cos^{-1}u= -\frac{1}{\sqrt{1-u²}}, (-1<u<1)

Arctan and Arccot Derivatives

($a$ and $n$ are constants and $u$ and $v$ are differentiable functions of $x$)

• $$\frac{d}{dx} \tan^{-1}u = \frac{1}{1+u²} \cdot \frac{du}{dx}$$

• $$\frac{d}{dx} \cot^{-1}u = -\frac{1}{1+u²} \cdot \frac{du}{dx}$$

Arcsec and Arccsc Derivatives

($a$ and $n$ are constants and $u$ and $v$ are differentiable functions of $x$)

• \frac{d}{dx} \sec^{-1}u = \frac{1}{|u| \sqrt{u²-1}} \cdot \frac{du}{dx}, (|u|>1)

• \frac{d}{dx} \csc^{-1}u = -\frac{1}{|u| \sqrt{u²-1}} \cdot \frac{du}{dx}, (|u|>1)

What is the relationship between differentiability and continuity?

“Differentiability implies continuity, but continuity does not imply differentiability”

Parametric First Derivative (BC)v

$\frac{dy}{dx} = \frac{\frac{dy}{dt}}{\frac{dx}{dt}}$ where $t$ is the parameter

Parametric Second Derivative (BC)

$$\frac{d²y}{dx²} = \frac{d}{dx}(\frac{dy}{dx}) = \frac{\frac{d}{dt}(\frac{dy}{dx})}{\frac{dx}{dt}}$$

Unit 4: Applications of Differential Calculus

• slopes of curves/eqs. of tangent lines

• maxima, minima, points of inflections

• increasing, decreasing, concave up and down

• motion along a line

• local linear approximations

• related rates

• slope of parametric and polar curves (BC)

• motion along parametrically defined curves (BC)

Slope of a curve

slope of the tanget to the curve at point $(x_1, y_1)$ is $f’(x)$ at $x=x_1$

Critical Point

• $f’(a)=0$ or $f’(a)=$ undefined

• if $f$ has a derivative everywhere, solve $f’(x)=0$

Equation of the tangent to a curve

(curve =$y=f(x)$ at point $P(x_1, y_1)$) is:

$$y-y_1=f’(x_1)(x-x_1)$$

• if the tangent is horizontal at a point, then the derivative = 0 (no slope=no rate of change=no derivative)

• if the tangent is vertical at a point, then the derivative does not exist

Tangents to Parametrically Defined Curves