Geometry Honors Semester 2 Finals

what is a diagonal?

A diagonal of a polygon is a segment that connects any two nonconsecutive vertices.

what is a parallelogram?

A parallelogram is a quadrilateral with both pairs of opposite sides parallel.

what is a rectangle?

A rectangle is a parallelogram with four right angles.

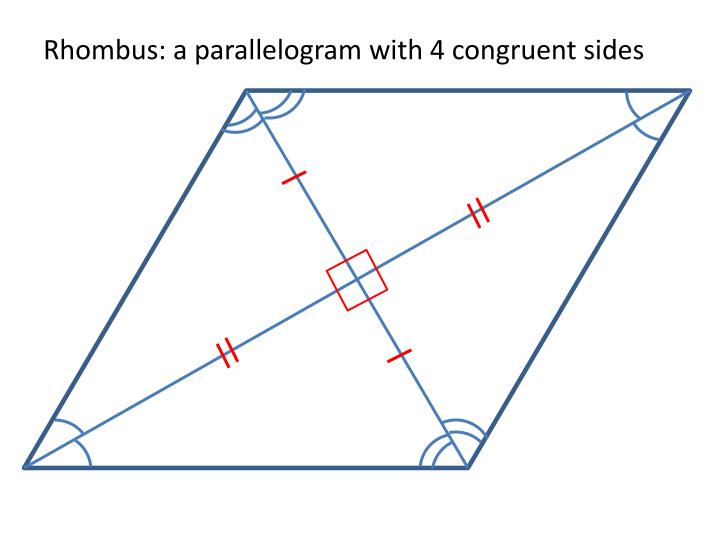
Rhombus Postulate

A rhombus is a parallelogram with all four sides congruent.

Square Postulate

A square is a parallelogram with four congruent sides and four right angles.

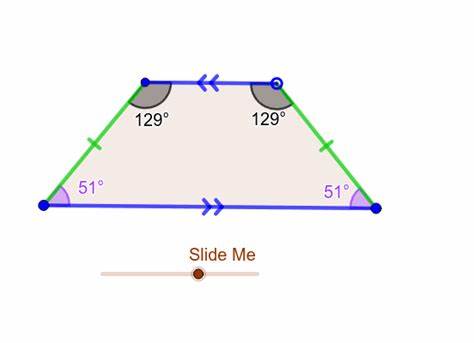
what is a trapezoid?

A trapezoid is a quadrilateral with exactly one pair of parallel sides. The parallel sides are called the bases. The nonparallel sides are called the legs. The base angles are formed by the base and one of the legs.

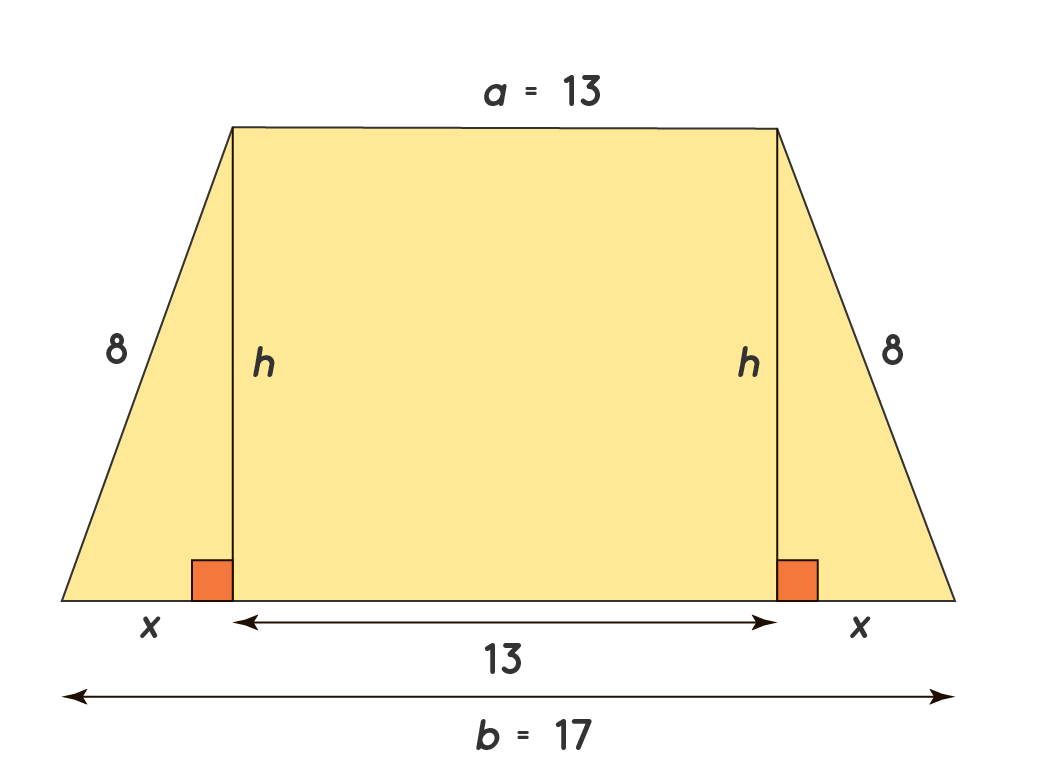
what makes a trapezoid isosceles?

If the legs of a trapezoid are congruent, then the trapezoid is an isosceles trapezoid.

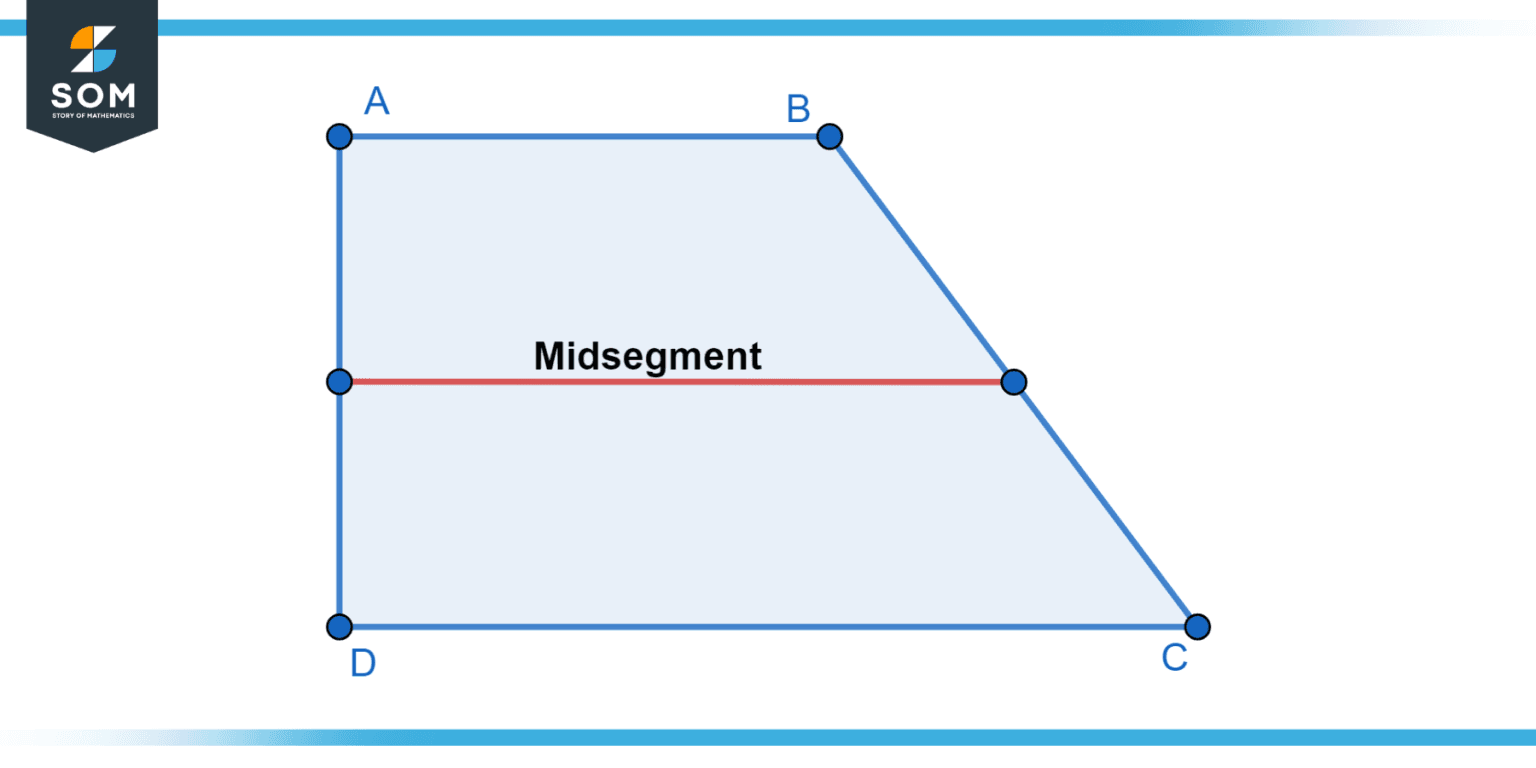
Midsegment of a Trapezoid Postulate

The midsegment of a trapezoid is the segment that connects the midpoints of the legs of the trapezoid.

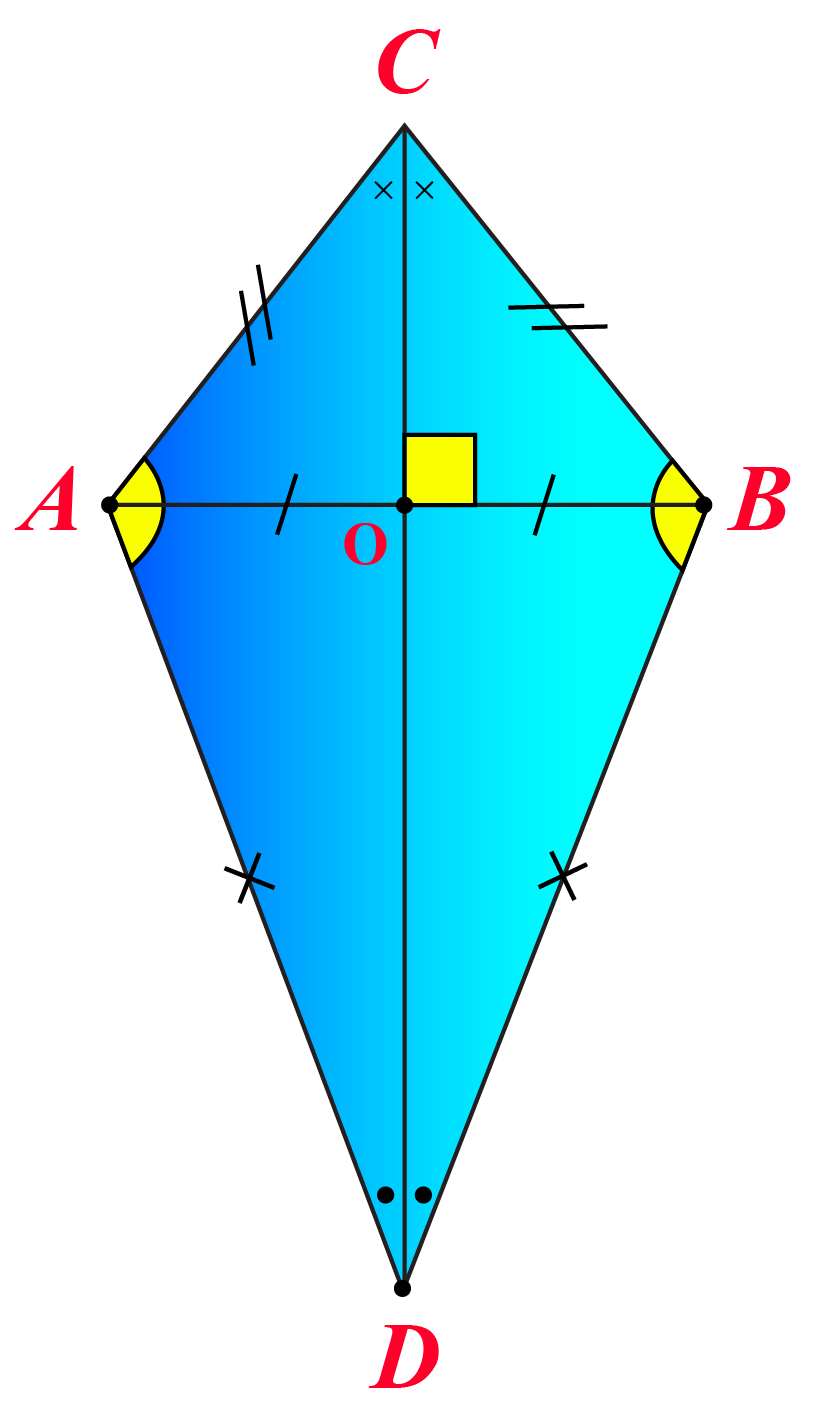
what is a a kite?

A kite is a quadrilateral with exactly two pairs of consecutive congruent sides.

what is sum of a polygon’s interior angles?

The sum of the interior angles of an n-sided convex polygon is (n-2)180.

what is the sum of a polygon’s exterior angles

The sum of the exterior angles of an n-sided convex polygon, one angle at each vertex, is 360.

If a quadrilateral is a parallelogram, (sides…)

then its opposite sides are congruent. 

if a quadrilateral is a parallelogram…(angles) (3 answers)

• then its opposite angles are congruent. 

• then its consecutive angles are supplementary. 

• If a parallelogram has one right angle, then it has four right angles.

If a quadrilateral is a parallelogram, (diagonals)

then its diagonals bisect each other.

If a parallelogram is a rectangle then..(diagonals)

its diagonals are congruent.

If a parallelogram is a rhombus, then…(diagonals)

its diagonals are perpendicular.

If a parallelogram is a rhombus, then each of the diagonals do what?

bisects a pair of opposite angles.

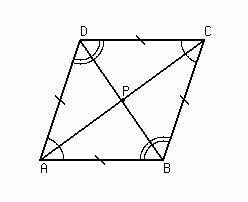
If the parallelogram is a rhombus then it has….(sides)

one pair of congruent consecutive sides

What happens if a quadrilateral is both a rectangle and a rhombus?

it is a square.

If a trapezoid is isosceles, then (angles)…

• each pair of base angles is congruent.

OR

• one pair of congruent base angles

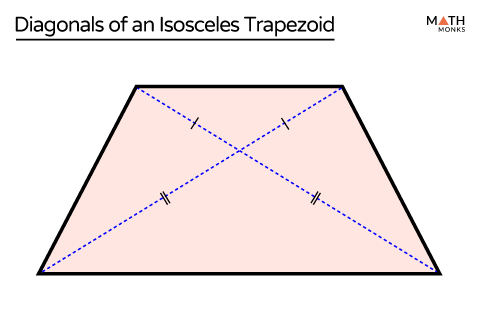
A trapezoid is isosceles if and only if (diagonals)…

its diagonals are congruent

what is the trapezoid midsegment theorem?

The midsegment of a trapezoid is parallel to each base and its measure is one half the sum of the lengths of the bases (the average of the bases).

If a quadrilateral is a kite, then (diagonals)…

its diagonals are perpendicular.

If a quadrilateral is a kite, then (angles)…

exactly one pair of opposite angles is congruent.

what is a ratio?

a comparison of two quantities using division.

what are extended ratios?

can be used to compare three or more quantities. (a:b:c means a:b, b:c, and a:c are ratios).

what is a proportion?

an equation stating that two ratios are equal.

what are means and extremes?

in the proportion the numbers a and d are called Extremes, and the numbers b and c are called Means.

what are cross products?

the product of the extremes and the product of the means

what are similar polygons?

polygons that have the same shape but not necessarily the same size.

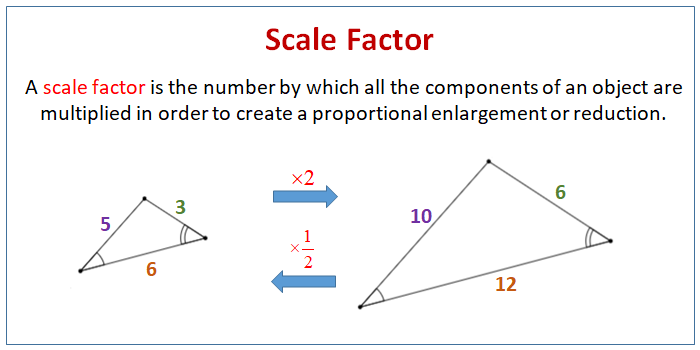
what is a scale factor?

the ratio of the lengths of the corresponding sides of two similar polygons.

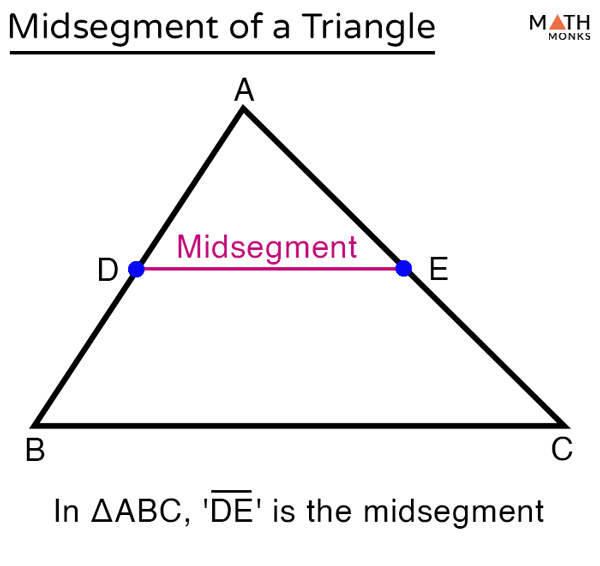
what is the midsegment of a triangle?

a segment with endpoints that are the midpoints of two sides of the triangle.

if two polygons are similar, then (perimeters)…

their perimeters are proportional to the scale factor between them.

Angle – Angle Similarity (AA~)

if two angles of one triangle are congruent to two angles of another triangle, then.. the △s are similar.

Side-Side-Side Similarity (SSS~)

If the corresponding side lengths of two triangles are proportional, then the triangles are similar.

Side-Angle-Side Similarity (SAS~)

If the lengths of two sides of one triangle are proportional to the lengths of two corresponding sides of another triangle and the included angles are congruent, then the triangles are similar.

Properties of Similarity

• Reflexive Property of Similarity – ΔABC ~ ΔABC.

• Symmetric Property of Similarity – If ΔABC ~ ΔDEF, then ΔDEF ~ ΔABC.

• Transitive Property of Similarity - If ΔABC ~ ΔDEF, and ΔDEF ~ ΔXYZ, then ΔABC ~ ΔXYZ.

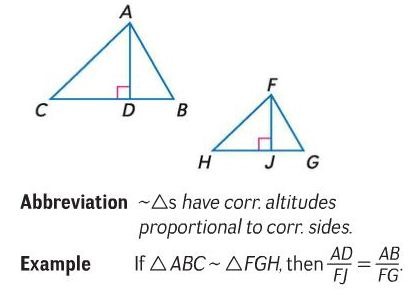
If two triangles are similar, the (altitudes)...

the lengths of corresponding altitudes are proportional to the lengths of corresponding sides

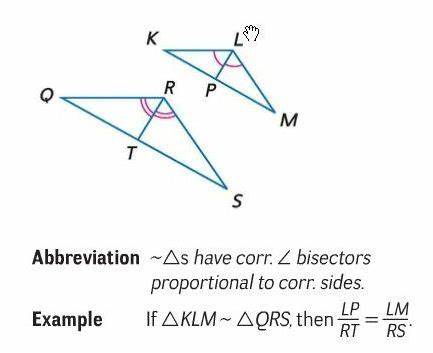
If two triangles are similar, the (angle bisectors)…

lengths of corresponding angle bisectors are proportional to the lengths of corresponding sides

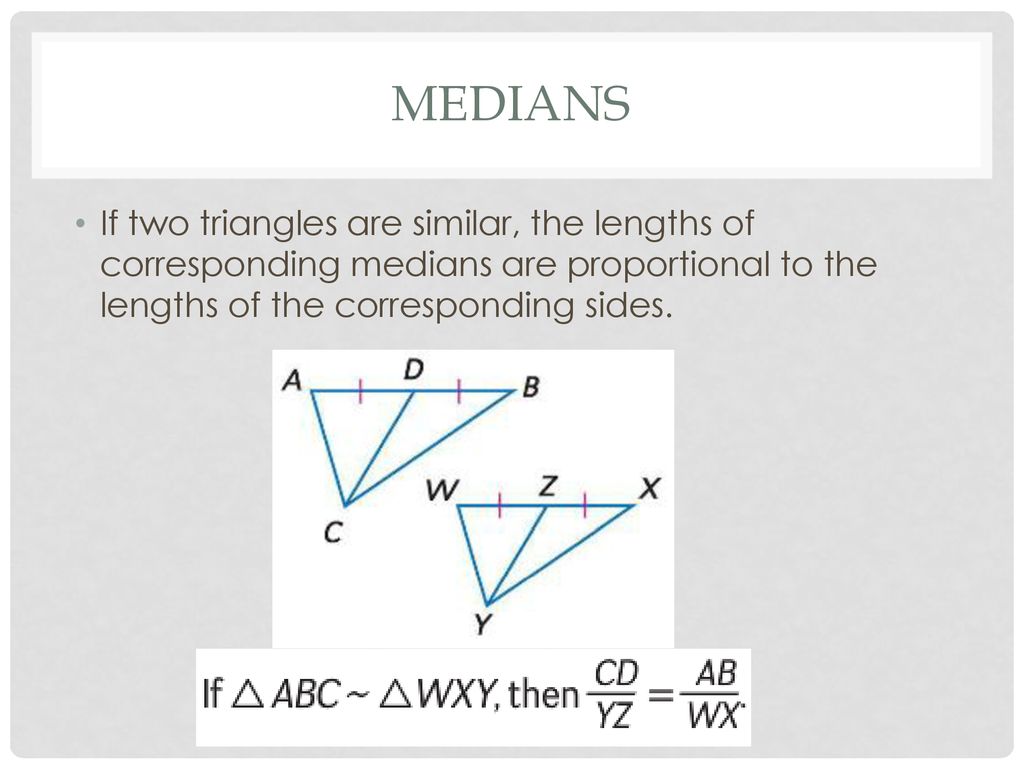
If two triangles are similar, the (medians)...

the lengths of corresponding medians are proportional to the lengths of corresponding sides

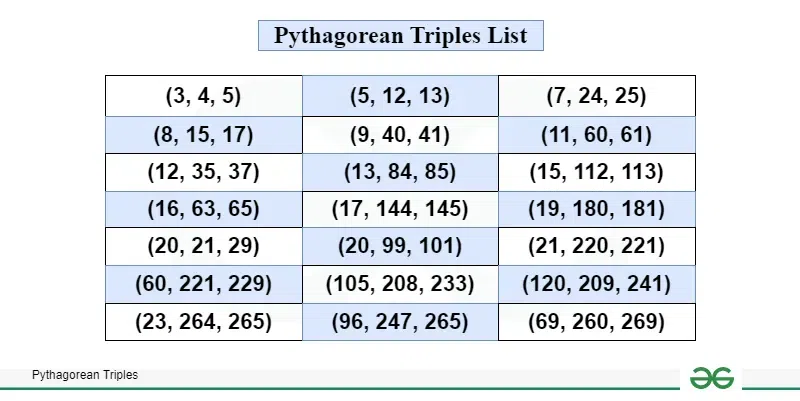
Pythagorean Triple

A set of three nonzero whole numbers a, b, and c such that a2+b2=c2.

Trigeomentry

The study of the properties of triangles and trigonometric functions and their applications.

Trigonometric Ratio

A ratio of the lengths of sides of a right triangle.

Angle of Elevation

The angle between the line of sight and the horizontal when an observer looks upward.

Angle of Depression

The angle between the line of sight and the horizontal when an observer looks downward.

A circle is …..

the locus or set of all points in a plane equidistant from a given point call the center of the circle.

A radius is….

a segment with endpoints at the center and on the circle.

A chord is….

a segment with endpoints on the circle.

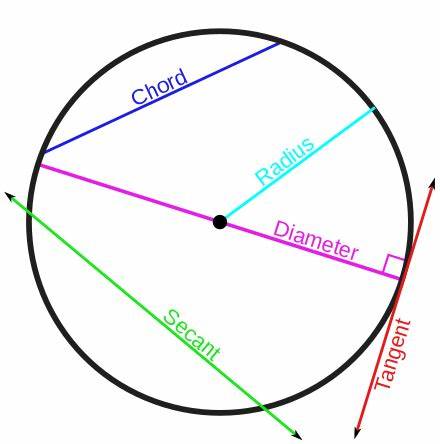
A diameter is….

a chord that passes through the center and is made up of collinear radii.

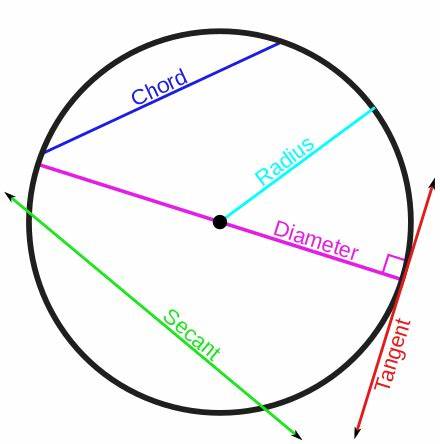
Concentric circles are…

are coplanar circles that have the same center.

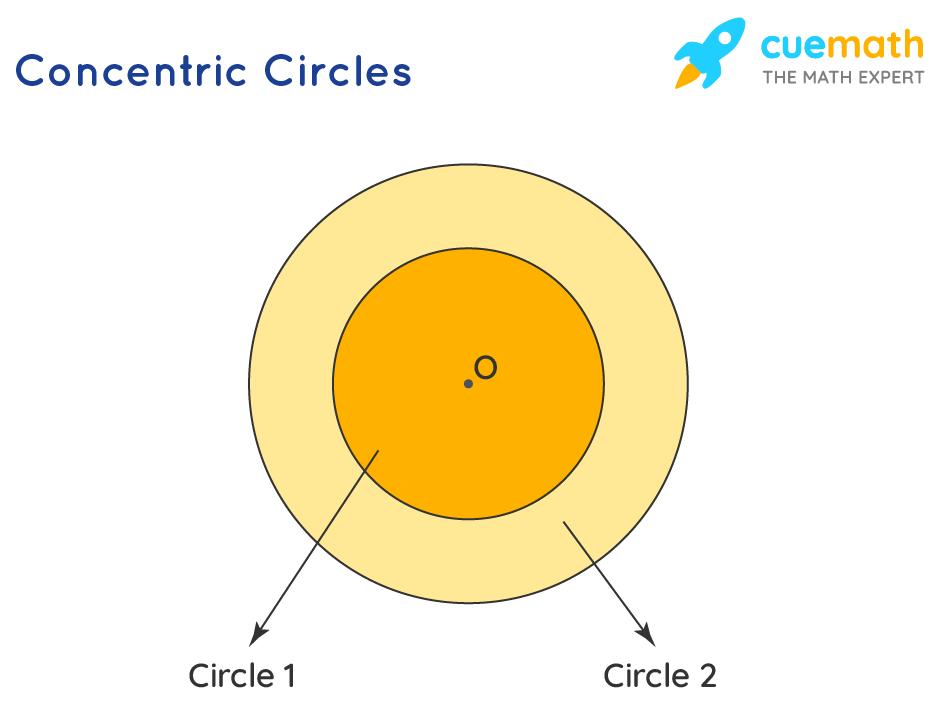
The circumference of a circle is

the distance around the circle.

If a polygon is inscribed about a circle…

if all of its vertices lie on the circle.

if a circle is circumscribed about a polygon…

it contains all the vertices of the polygon.

A central angle of a circle is….

an angle with a vertex in the center of the circle.

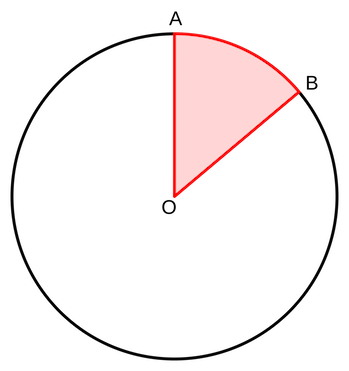
An arc is…

a portion of a circle defined by two endpoints.

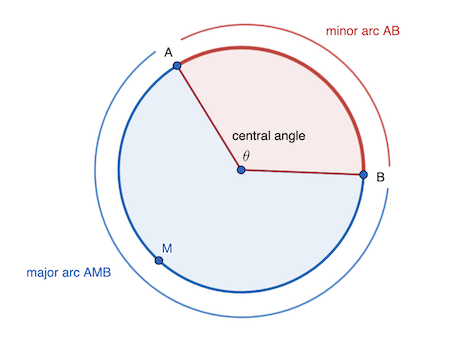
A minor arc is….

the shortest arc connecting two endpoints on a circle.

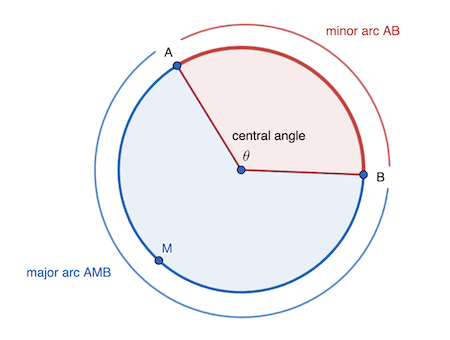
A major arc is

the longest arc connecting two endpoints on a circle.

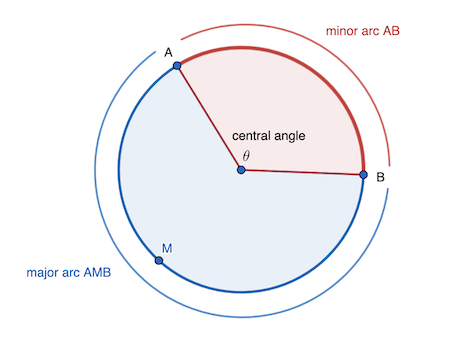
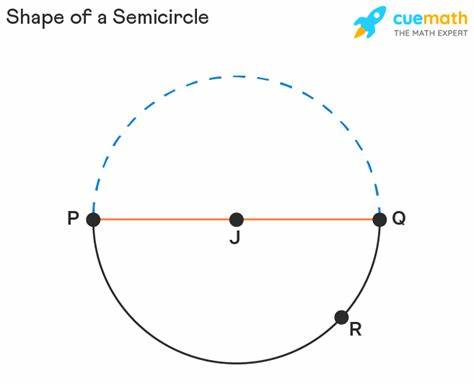
A semicircle is…

an arc with endpoints that lie on a diameter.

Congruent arcs are ….

arcs in the same or congruent circles that have the same measure.

Adjacent arcs….

are arcs in a circle that have exactly one point in common.

Arc length is….

the distance between endpoints along an arc measured in linear units.

An inscribed angle …

has a vertex on a circle and sides that contain chords of the circle.

An intercepted arc has…

endpoints on the sides of an inscribed angle and lies in the interior of the inscribed angle.

A tangent is….

a line in the same plane as a circle that intersects the circle in exactly one point called the point of tangency.

A common tangent is ….

a line, ray or segment that is tangent to two circles in the same plane.

A secant is ….

a line that intersects a circle in exactly two points.

Chord segments are …

the segments each chord is divided into when two chords intersect inside a circle.

A secant segment is…

a segment of a secant line that has exactly one endpoint on the circle.

A secant segment that lies in the exterior of the circle is ….

called an external secant segment.

A tangent segment is…

a segment of the tangent with one endpoint on the circle.

what is the Arc Addition Postulate?

The measure of an arc formed by two adjacent arcs is the sum of the measures of the two arcs.

two minor arcs are congruent if and only if (central angles)

their central angles are congruent.

two minor arcs are congruent if and only if (chords)

their corresponding chords are congruent.

If a diameter or radius of a circle is perpendicular to a chord, then….

it bisects the chord and its arc.

two chords are congruent if and only if

they are equidistant from the center.

what is the Inscribed Angle Theorem

If an angle is inscribed in a circle, then the measure of the angle equals ½ the measure of its intercepted arc.

If two inscribed angles of a circle intercept the same arc or congruent arcs, then

he angles are congruent.

An inscribed angle of a triangle intercepts a diameter or semicircle if and only if

the angle is a right angle.

If a quadrilateral is inscribed in a circle, then

its opposite angles are supplementary.

In a plane, a line is tangent to a circle if and only if

it is perpendicular to a radius drawn to the point of tangency.

If two segments from the same exterior point are tangent to a circle, then

they are congruent.

If two secants or chords intersect in the interior of a circle, then

the measure of an angle formed is one half the sum of the measure of the arcs intercepted by the angle and its vertical angle.

If a secant and a tangent intersect at the point of tangency, then

the measure of each angle formed is one half the measure of its intercepted arc.

If two secants, a secant and a tangent, or two tangents intersect in the exterior of a circle, then

the measure of the angle formed is one half of the difference of the measures of the intercepted arcs.

If two chords intersect inside a circle, then

the products of the lengths of the chord segments are equal.

If two secants intersect in the exterior of a circle, then

the product of the measures of one secant segment and its external secant segment is equal to the product of the measures of the other secant and its external secant segment.

If a tangent and a secant intersect in the exterior of a circle, then

the square of the measure of the tangent is equal to the product of the measures of the secant and its external secant segment.

Base of a parallelogram –

Any side of a parallelogram.

Height of a parallelogram -

The perpendicular distance between any two parallel bases.

Base of a triangle –

Any side of a triangle.

Height of a triangle/trapezoid –

The length of an altitude drawn to a given base.

Sector of a circle –

A region of a circle bounded by a central angle and its intercepted arc.

Center of a regular polygon .

The center of a circle circumscribed about the polygon

Radius of a regular polygon

The radius of a circle circumscribed about the polygon.

Apothem –

A segment that is drawn from the center of a regular polygon perpendicular to a side of the polygon.

Central Angle of a Regular Polygon –

An angle that has its vertex at the center of a polygon and with sides that pass through consecutive vertices of the polygon.

Area Addition Postulate –

The area of a region is the sum of the areas of its nonoverlapping parts.

Area Congruence Postulate

If two figures are congruent, then they have the same area.

Areas of Similar Polygons –

If two polygons are similar, then their areas are proportional to the square of the scale factor between them.