Topic 1 - Quantization of Energy: Wave-Particle Duality and the Photo-Electric Effect

Photons

Discrete packets (quantized) of light energy 

Quantum Mechanics: Wave-Particle Duality

Discovered that:

• Light (waves) shows particle-like properties. 

• Small particles (e.g., electrons) show wave-like (light) properties.

1. Photons — Photons absorbed/emitted by atoms, molecules, or surfaces when they increase/decrease in energy. This is the basis of spectroscopy.

• When atoms/molecules gain energy → photon is absorbed

• When atoms/molecules lose energy → photon is emitted

2. Electrons — Not point particles orbiting a nuclei but wavefunctions/orbitals with shape (s, p, d, f) and quantised energy (energy levels)

Orbitals/Wavefunctions

Specific regions around a nucleus where electrons are most likely to be found.

Photon Properties in Quantum Mechanics

• Massless

• Chargeless

• Energy is quantized into discrete packets “quanta” proportional to frequency, as opposed to being continuous in classical mechanics

Photoelectric Effect - Hertz's Observation (1887)

• Light of sufficiently high frequency ejects electrons from a metal surface, when shined upon it.

• Key findings:

  • Below a frequency threshold → no electrons emitted 

  • Threshold varies for different metals.

  • Increasing intensity (brightness) without meeting threshold → no effect

    • Contradicts classical physics as it proposed that electrons would be released when the intensity of light was further increased.

Intensity (Brightness)

• Classical Mechanics: The amplitude of the wave.

• Quantum Mechanics: The amount of photons hitting the surface per second.

Photoelectric Effect - Einstein’s Explanation

• E = hν

• Alternative formula: E = hc/λ

  • E in Joules (J)

  • v in Hertz (Hz)

  • h = 6.626 x 10^-34  J/s (Planck Constant)

• Photon energy depends on (proportional to) frequency, not intensity.

• Photon energy is inversely proportional to the wavelength.

Photoelectric Effect - Frequency Dependence Equation

• E = hν

• Alternative formula: E = hc/λ

  • E in Joules (J)

  • v in Hertz (Hz)

  • h = 6.626 x 10^-34  J/s (Planck Constant)

Wave Equation

c = λν (c = 2.998 × 10⁸ m/s)

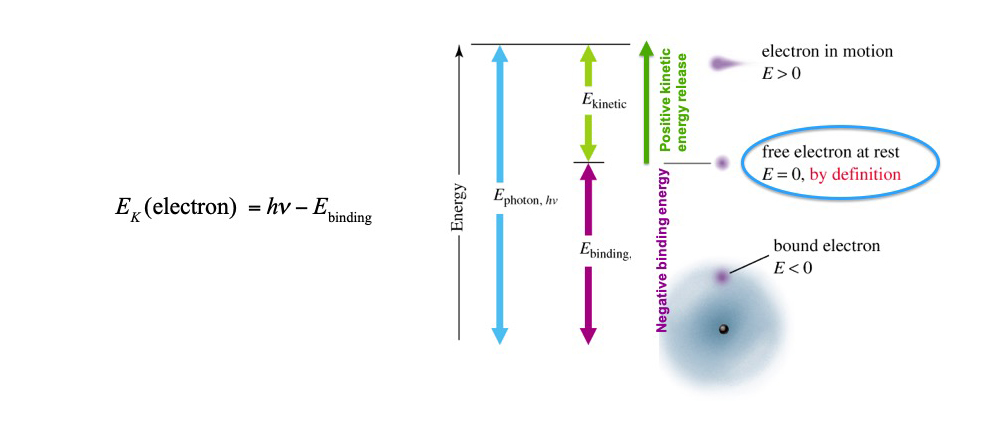
Photoelectric Effect - Electron Kinetic Energy Equation

E_k = E_photon(hv) - E_binding

Calculates the energy of the electron ejected from the atom (bound → free)

Photoelectric Effect - Electron Kinetic Energy's Atomic Structure

• Binding energy (energy for an electron bound to a metal) depends on the atom/metal.

• One excess photon energy beyond binding energy → is capable of liberating one electron = kinetic energy of ejected electron.

  • Insufficient energy = no electron ejected.

  • Just enough energy = electron ejected + small kinetic energy.

  • Plenty of energy = electron ejected + large kinetic energy.

• Free electron at rest has zero kinetic energy, hence the binding energy has negative (-) value and the kinetic energy has (+) value.

Tips

• The binding energy can also be called a work function.

• Under certain conditions, the binding energy can also be referred to as ionization energy.