Physics Quarterly

What is intertia?

Objects cannot move or change its state of motion

What is inertia of rest?

Inability of an object to change its state of rest

\
Example: A book lying on a table until pushed

A stationary bus beginning to move

Inertia of motion

Inability of an object to change its state of uniform speed on its own

\
Examples: An athlete finishing a race will continue to run past the finish line

A ball will continue rolling if pushed

Inertia of direction

Inability of an object to change its direction of motion on its own

\
Examples: A bus moring along a straight line takes a turn to the right and the passengers move left

\
A stone and a string is whirling and if the string is suddenly cut the stone will not continue to move in a circular but will move tangential to the circle

What is Newtons second law?

The force acting on an object is equal to the rate of change of its momentum

What is one newton?

The force that acts on 1kg of mass to give an acceleration 1ms^-2 in the direction of the force

Show it is easier to pull an object than to push it using the free body diagram

When a body is pushed at an arbitrary angle θ the applied force F can be split into two parts as F sin 0 parallel to the surface and F cos 0 perpendicular to the surface.

Total downward force acting on the body is mg+F cos θ.

This means the normal force acting on the body increases

The maximal static friction also increases. Greater force needs to be applied to push the object into motion.

When pulled at angle θ, the applied force is resolved into two pieces. The total downward force acting on the object less than the total force when pushed. Therefore, it is easier to pull an object than to push it

What are the types of friction?

Static Friction (opposes the initiation of motion)

\
Kinetic Friction (force exerted by surface when an object slides)

How can you reduce friction?

* using lubricants
* polishing
* stream lining
* ball bearings

What does pseudoforce mean?

a force with no origin

* arises due to the non-inertial nature of the frame considered

Empirical laws of friction

* friction is independant of surface of contact
* coefficiant of kinetic friction is less than coefficient of static friction
* directional of frictional force is always opposite to the motion of one body over the other
* always acts on the object parallel to the surface on which the object is placed
* magnitude of frictional force between any two bodies in contact is directly proportional to the normal reaction between them

What is Newton’s third law?

For every action there is an equal and opposite reaction

What is an inertial frame?

The one in which if there is no force on the object the object moves at constant velocity

What are concurrent forces?

A collection of forces called concurrent if the lines of forces act at a common point

What is Lami’s theorem

If a system of three concurrent and coplanar forces is in equilibrium, than the magnitude of each force is proportional to the sine of the angle between the other two forces

Explain the motion of blocks connected by a string in vertical motion and horizantal motion

When objects are connected by strings and a force F is applied either vertically or horizantally or along an inclined plane it produces a tension T in the string, which affects the acceleration to an extent

What is the origin of friction?

It is the opposing force exerted by the surface on an object.

What is the significance of Newton’s Laws?

* Newton's Laws of Motion describe the fundamental principles of motion and forces.
* essential for understanding and predicting the behavior of objects in motion.
* basis for classical mechanics and are used in various fields, including engineering, physics, and everyday life.

Centripetal vs. Centrifugal Force

**Centripetal**

* a real force
* acts in inertial and non-inertial frames
* acts toward the axis of rotation/center of circle in circular motion
* origin of centripetal force is interaction between two objects
* must be included in inertial frames when drawing free bodies

\
**Centrifugal**

* pseudo force
* acts only in non-inertial frames
* acts outward from axis of rotation/center of circular motion
* origin in inertia
* does not arise from interaction

\

Centrifugal force

* pseudo force
* acts only in non-inertial frames
* acts outward from axis of rotation/center of circular motion
* origin in inertia
* does not arise from interaction

What is Newton’s First Law?

Every object continues to be in the state of rest or of uniform motion (constant velocity) unless there is external force acting on it

What is Newton’s Second Law?

The force acting on an object is equal to the rate of change of its momentum

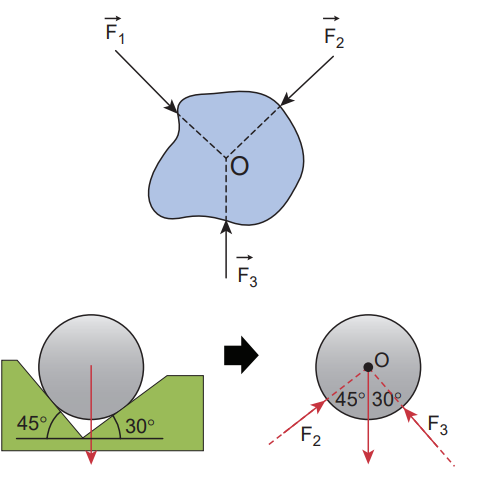
What is concurrent force?

When lines of forces act at a common point

Conserved Force

• conserves the total mechanical energy of a system.

• When doing work the total mechanical energy of the system remains constant

• The most common example of a conserved force is gravity. In the absence of air resistance and other external factors, gravity conserves the mechanical energy of an object as it moves up and down in a gravitational field.

• The sum of kinetic energy (KE) and potential energy (PE) remains constant: KE + PE = constant.

Nonconserved Force

• does not conserve the total mechanical energy of a system.

• When doing work, the total mechanical energy of the system changes.

• Friction is a common example of a non-conserved force. When an object moves across a surface with friction, some of its mechanical energy is converted into heat due to the work done against friction, resulting in a decrease in mechanical energy.

• The sum of kinetic energy (KE) and potential energy (PE) is not constant: KE + PE may decrease over time due to the work done by the non-conserved force.

Conserved vs. Nonconserved Force

The distinction between conserved and non-conserved forces is based on whether the force conserves or changes the total mechanical energy of a system.

Moment of Inertia

The moment of inertia of a rigid body is the sum of moments of inertia of all such individual point masses that constitute the body

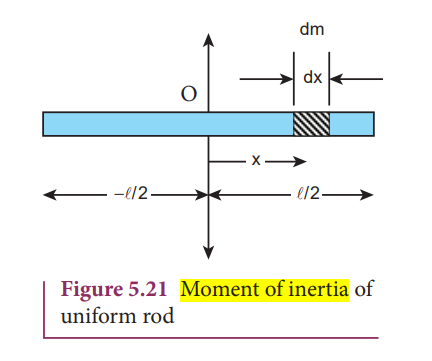
Moment of Inertia of a Uniform Rod

• fix an origin at the centre of mass

• take an infinitely small mass (dm) at distance (x) from the origin

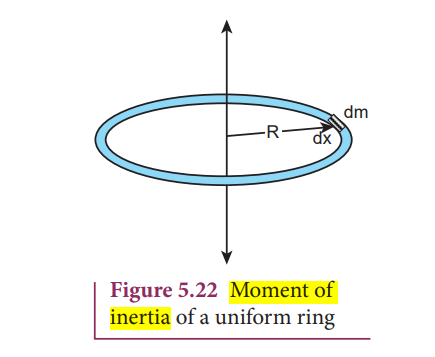
Moment of Inertia of a Uniform Ring

• take an infinitely small mass (dm) of length (dx) of the ring

• Dm is distance R (radius of the ring from the axis)

[

Moment of Inertia of a Uniform Disk

• consider ring of mass (dm) and thinkness (dr) and radius ®

Moment of Inertia (dI) is

dI=(dm)r

Parallel Axis Theorem

The moment of inertia of a body about any axis is equal to the sum of its moment of inertia about a parallel axis through its centre of mass and the product of the mass of the body and the square of the perpendicular distance between the two axes

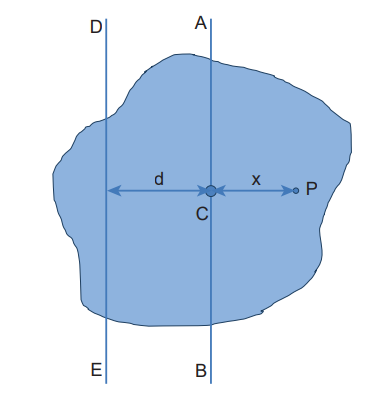
Perpendicular Axis Theorem

The theorem states that the moment of inertia of a plane laminar body about an axis perpendicular to its plane is equal to the sum of moments of inertia about two perpendicular axes lying in the plane of the body such that all the three axes are mutually perpendicular and have a common point

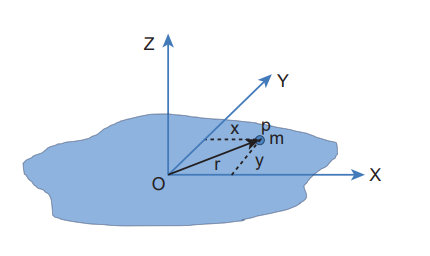
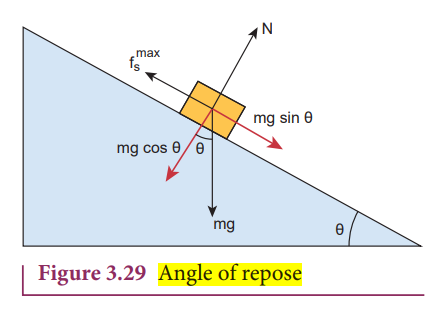
Angle of Repose

The angle of inclined plane with the horizontal such that an object placed on it begins to slide