Medical Genetics - Chapter 4: Autosomal Dominant and Recessive Inheritance

A man who has achondroplasia marries a phenotypically normal woman. If they have four children, what is the probability that none of their children will be affected with this disorder? What is the probability that all of them will be affected?

Because this is an autosomal dominant disorder, and because affected homozygotes die early in life, the man is a heterozygote and has a 50% chance of passing the disease-causing allele to each of his offspring.

The probability that all four will be affected is given by the product of each probability: (1/2)4 = 1/16.

The probability that none will be affected (1/16) is obtained in exactly the same way

The estimated penetrance for familial retinoblastoma is approximately 90%. If a man has had familial retinoblastoma and mates with a woman who does not have a retinoblastoma mutation, what is the risk that their offspring will develop retinoblastoma?

The probability that the offspring will inherit the retinoblastoma susceptibility allele is 0.50, because familial retinoblastoma is an autosomal dominant disease. However, we must also consider the penetrance of the disorder. The probability of both inheriting the disease-causing allele (0.50) and expressing the disease phenotype (0.90) is given by multiplying the two probabilities together: 0.90 × 0.50 = 0.45.

A 30-year-old woman had a sister who died from infantile Tay-Sachs disease, an autosomal recessive disorder that is fatal by age 6 years. What is the probability that this woman is a heterozygous carrier of the Tay-Sachs mutation?

Because the woman’s sister had Tay–Sachs disease, both parents must be heterozygous carriers. This means that, at birth, one fourth of their offspring will be affected, one half will be carriers, and one fourth will be genetically normal. Note, however, that the woman in question is 30 years old. She cannot possibly be an affected homozygote because affected individuals die by age 6 years.

A man has neurofibromatosis type 1. His mother also has this condition. What is the probability that his sister also has this disease?

b) In the absence of knowledge of his sister's phenotype, what is the probability that his sister's daughter has neurofibromatosis type 1?

Because the mother has neurofibromatosis and can be assumed to be a heterozygote (homozygotes for this condition have not been reported), the probability that her daughter (the man’s sister) inherits the disease-causing allele is 1/2.

b) The probability that the sister transmits the disease-causing allele to her daughter is again 1/2, so the probability that both events occur is 1/2 × 1/2 = 1/4.

If we knew that the man’s sister was affected, then the probability that his sister’s daughter is affected is simply 1/2.

Consider a woman who is a known heterozygous carrier of a mutation that causes PKU (autosomal recessive).

a) What is the probability that her two grandchildren, who are first cousins, are both heterozygous carriers of this PKU-causing allele? b) Suppose instead that the woman is affected with PKU. Now what is the probability that both of her grandchildren carry the disease-causing allele

The probability that the woman’s disease-causing allele is transmitted to her offspring is 1/2, and the probability that this offspring in turn transmits the disease-causing allele to his or her offspring (i.e., the grandchild) is again 1/2. Thus, the probability that one grandchild has inherited the allele is 1/2 × 1/2, or 1/4.

Similarly, the probability that the other grandchild has inherited the allele is 1/4. The probability that both grandchildren have inherited the allele is 1/4 × 1/4 = 1/16.

b) If the grandmother has PKU, she must be homozygous for the disease-causing allele. Thus, both of her children must be heterozygous carriers (probability = 1). The probability that one of these individuals transmits the disease-causing allele to their offspring is 1/2. The probability that they both transmit the disease-causing allele to their offspring (i.e., that both grandchildren are heterozygous carriers) is 1/2 × 1/2 = 1/4.

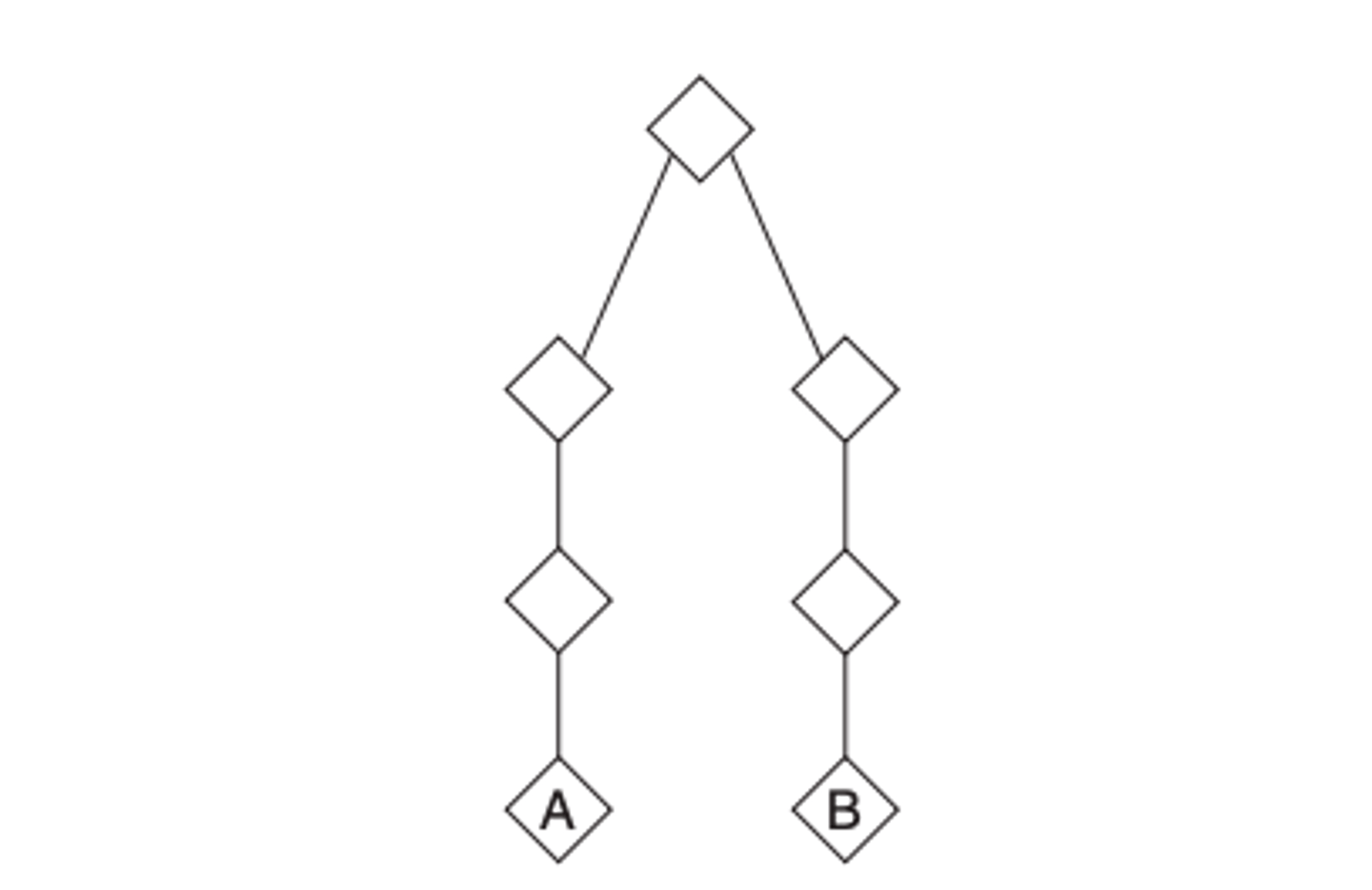
Two mating individuals labeled A and B, share a single great-grandparent. What is their coefficient of relationship?

Suppose that one member of this couple is a heterozygous carrier for PKU. What is the probability that this couple will produce a child affected with PKU?

The coefficient of relationship is (1/2)6 , or 1/64.

This gives the probability that the second member of the couple carries the PKU allele. The probability that two carriers will produce an affected offspring is 1/4. The overall probability that this couple will produce a baby affected with PKU is given by multiplying the probability that the mate also carries the allele (1/64) by the probability that the couple both transmit the allele to their offspring (1/4): 1/64 × 1/4 = 1/256. This demonstrates that the probability of producing an affected offspring in this consanguineous mating is actually quite small.

A suspect in a rape case has been typed for three STR (short tandem repeat) loci. His alleles match those of the evidentiary sample (semen taken from the rape victim) for each locus. He is a heterozygote for the first two loci and a homozygote for the third. The allele frequencies for locus 1 in the general population are 0.05 and 0.10. For locus 2, they are 0.07 and 0.02. For locus 3, the allele frequency in the general population is 0.08. What is the probability that a random individual in the general population would match the evidentiary sample?

The frequency of the heterozygote genotype in the general population is given by 2pq, according to the Hardy-Weinberg law. Thus, the frequency of the first genotype in the general population is predicted to be 2 × 0.05 × 0.10 = 0.01. Similarly, for the second system, the frequency of heterozygotes in the general population is 2 × 0.07 × 0.02 = 0.0028. The perpetrator was a homozygote for the third system; the frequency of the homozygote genotype in the general population is given by p2 , or 0.082 = 0.0064. If we can assume independence of the three STR loci in the general population, we can then multiply the frequencies of the three genotypes together to get the probability that a randomly chosen individual in the general population would have the same genotypes as the perpetrator.We thus multiply 0.01 × 0.0028 × 0.0064 to obtain a probability of 0.000000179, or 1/5,580,357. This probability can be made smaller by typing additional loci.

A man implicated in a paternity suit has had his DNA tested to establish whether or not he is the father of the baby. Four STR loci were tested for him, the mother, and the baby. The baby's alleles and the man's alleles match for all four loci. The frequencies of these alleles in the general population are 0.05, 0.01, 0.01, and 0.02.What is the probability that someone else in the general population could be the father of the baby?

We assume independence of the four STR loci. In this case, we multiply the four allele frequencies together to get the probability: 0.05 × 0.01 × 0.01 × 0.02 = 0.0000001 = 1/10,000,000.

In the paternity case, the father has contributed only half of the baby’s genotype at each locus, the other half being contributed by the mother. Thus, we examine only a single allele for each locus. We need to know the frequency of each genotype in the general population. We use the Hardy–Weinberg law to estimate the population frequency of each genotype, based on the known allele frequencies.