AP Calculus BC Formula Sheet Terms
1/93
Earn XP
Description and Tags
Quiz 1: 1-18, Quiz 2: 1-51, Quiz 3: 1-60, Quiz 4: 1-84, Quizzes 5 and 6: 1-94
Name | Mastery | Learn | Test | Matching | Spaced |
|---|
No study sessions yet.
94 Terms
Definition of e
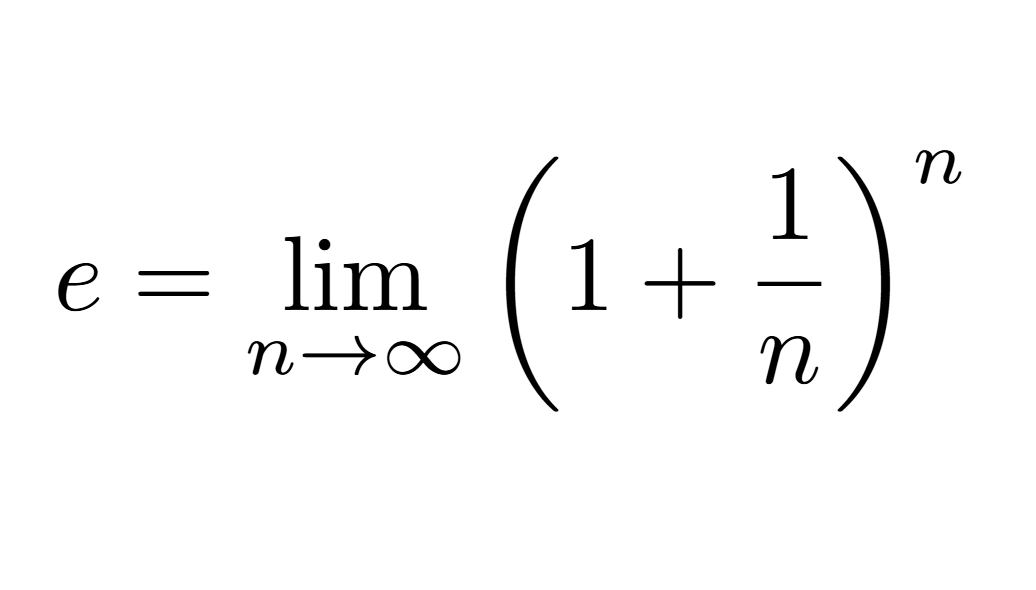
Absolute value
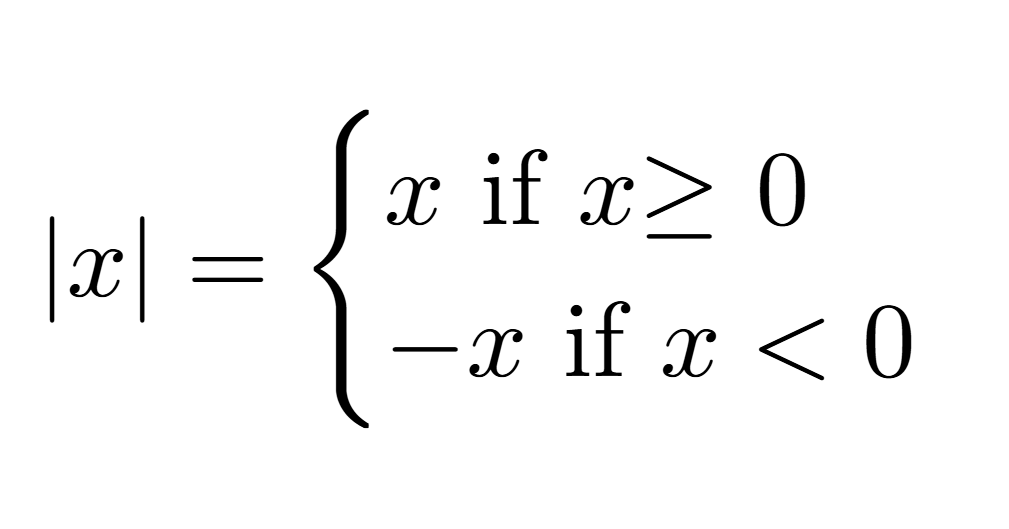
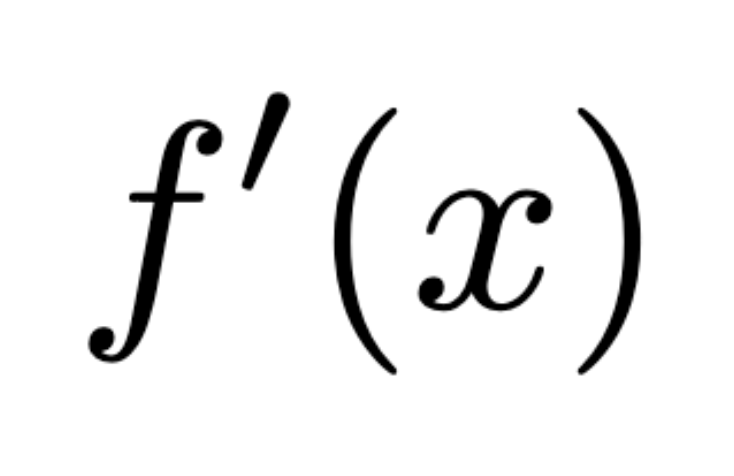
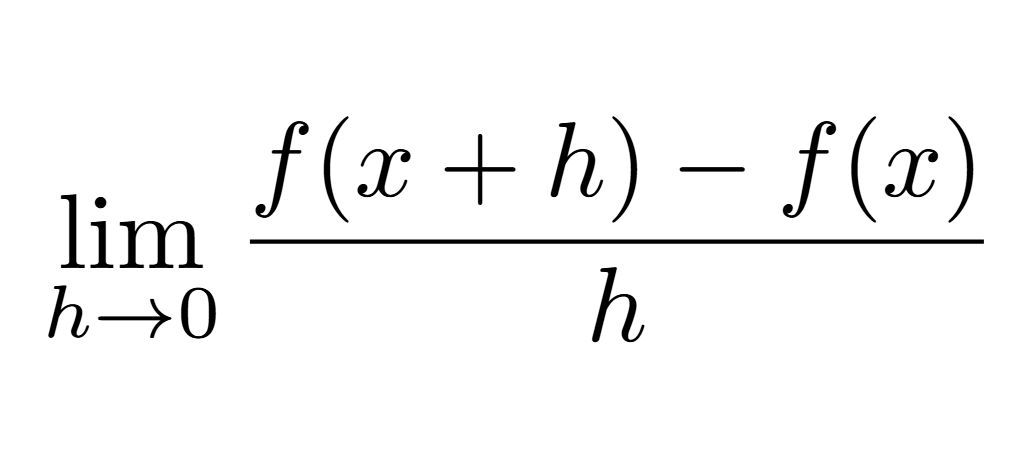
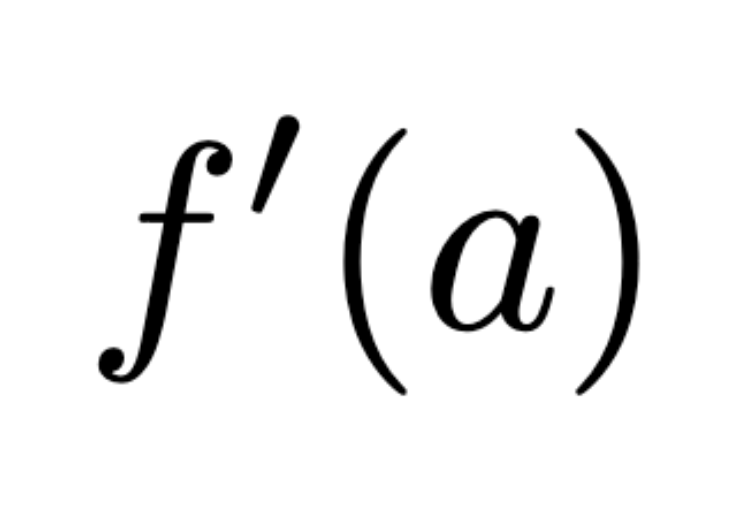
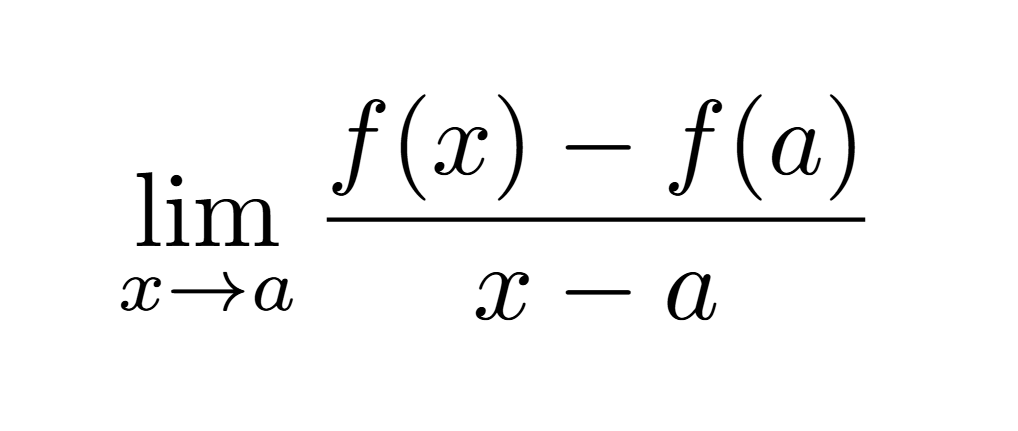
Definition of continuity
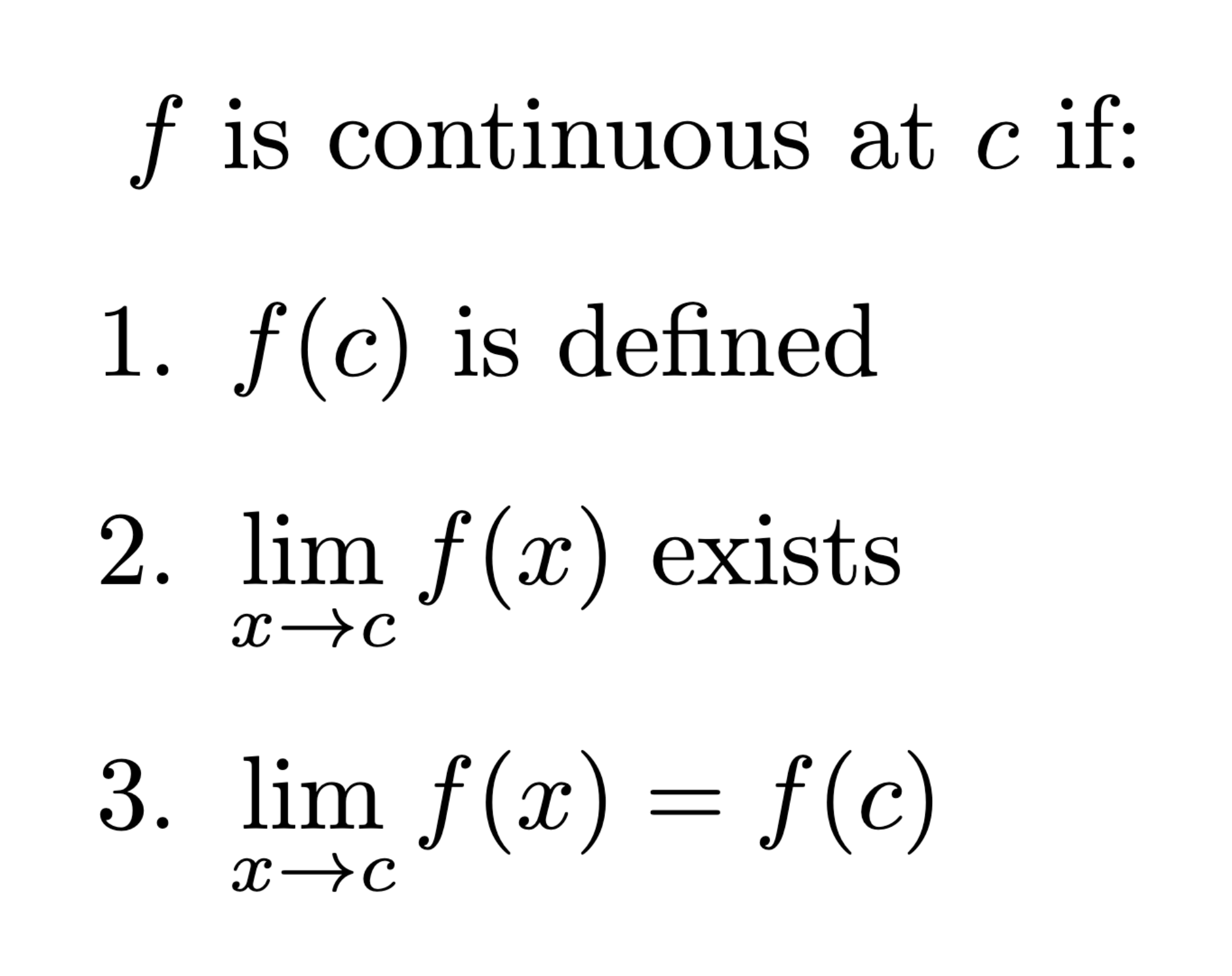
Average rate of change of f(x) on [a,b]
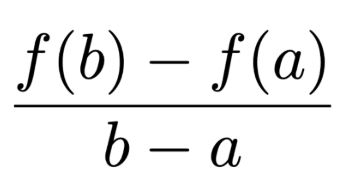
Average value of f(x) on [a,b]
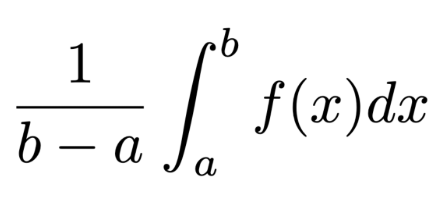
Rolle’s Theorem

Mean Value Theorem
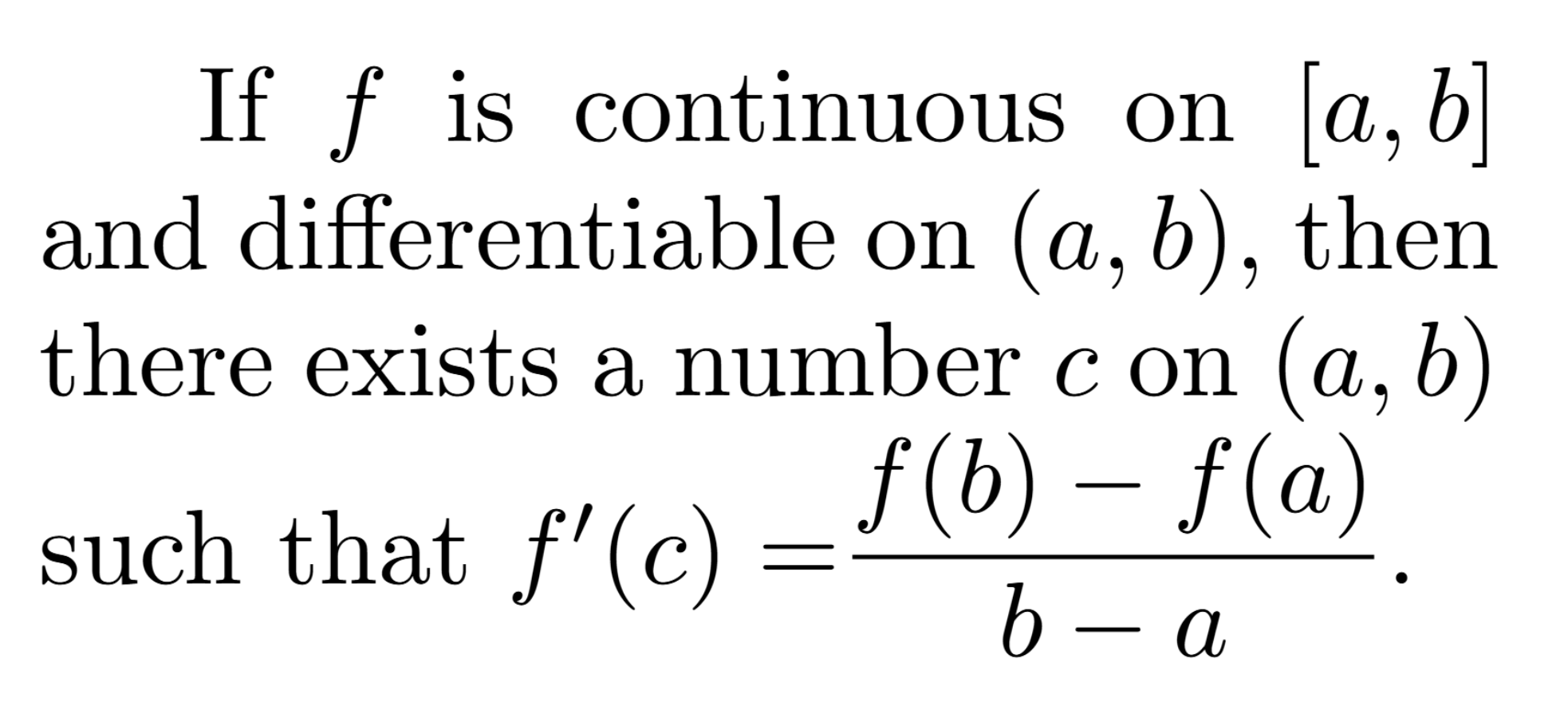
Intermediate Value Theorem

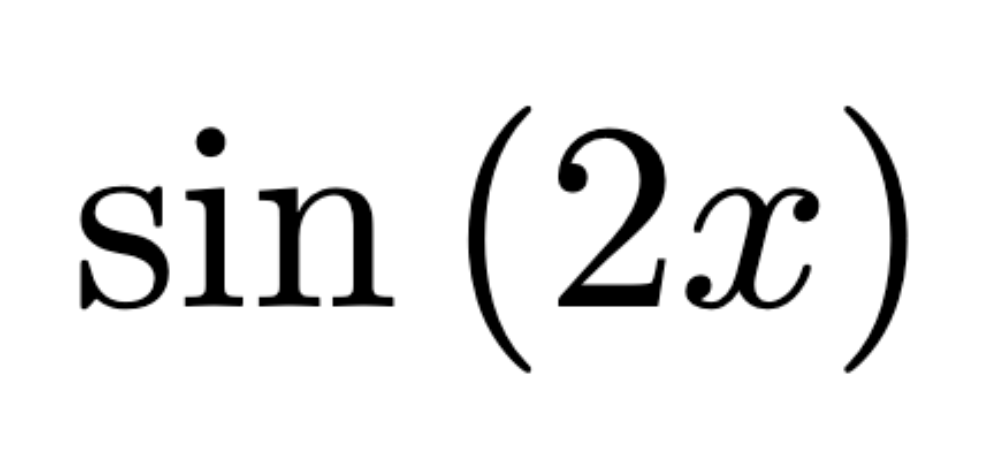
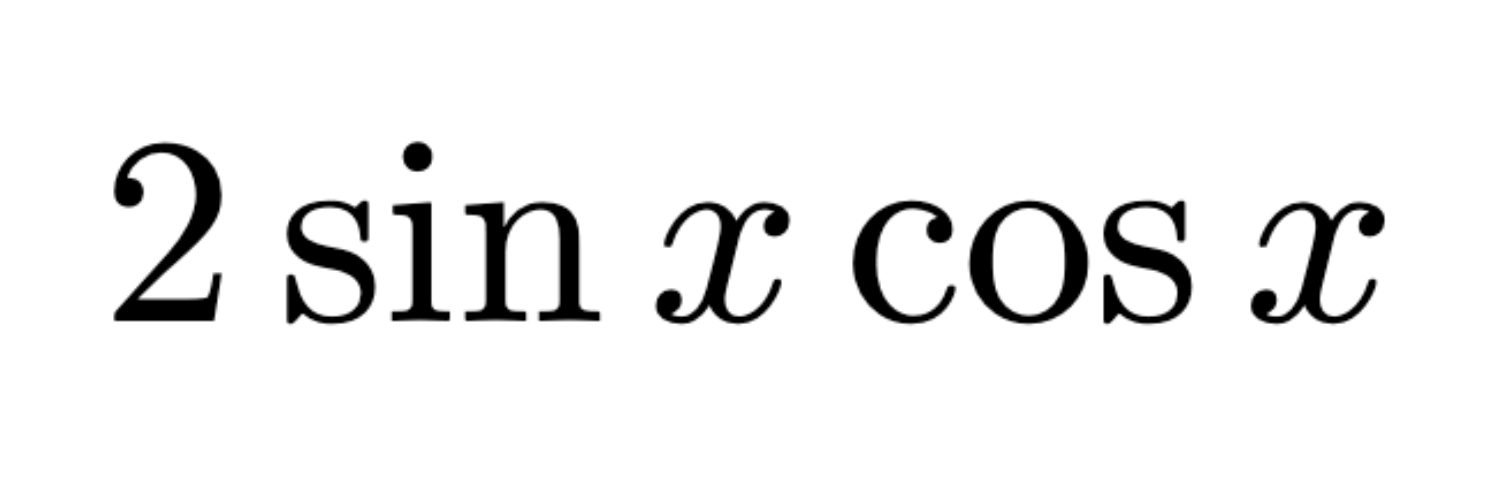
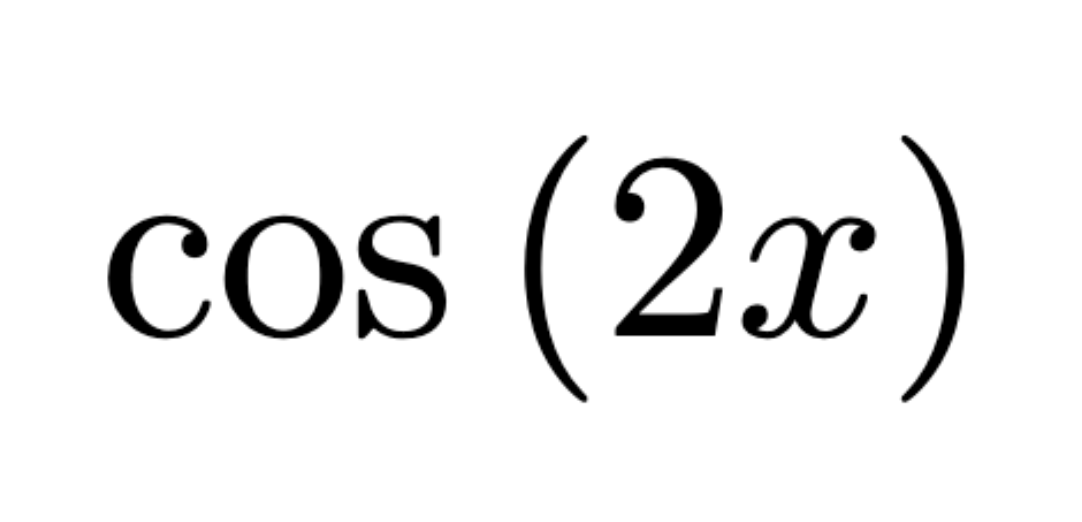
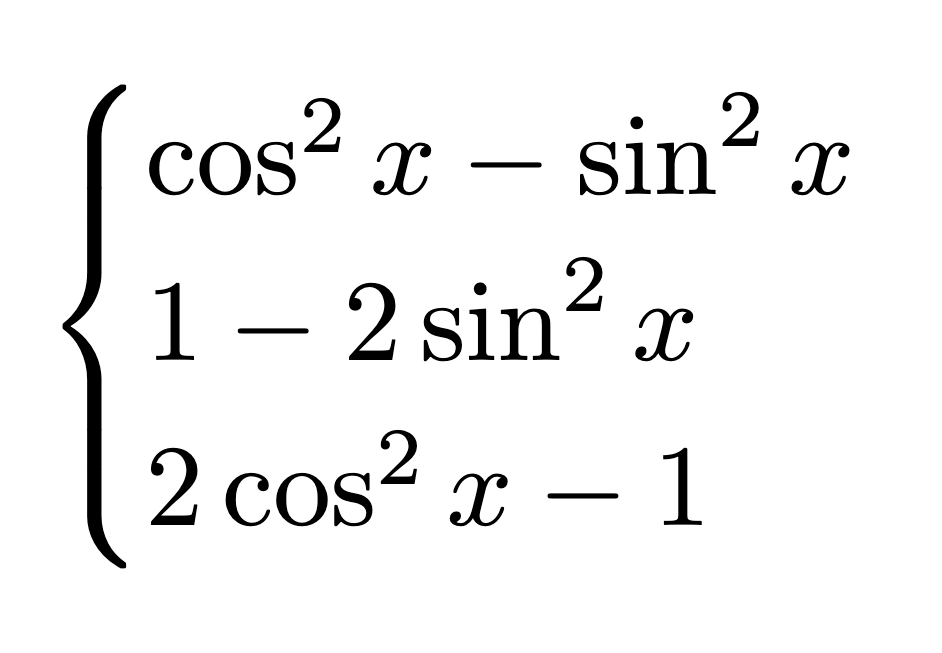
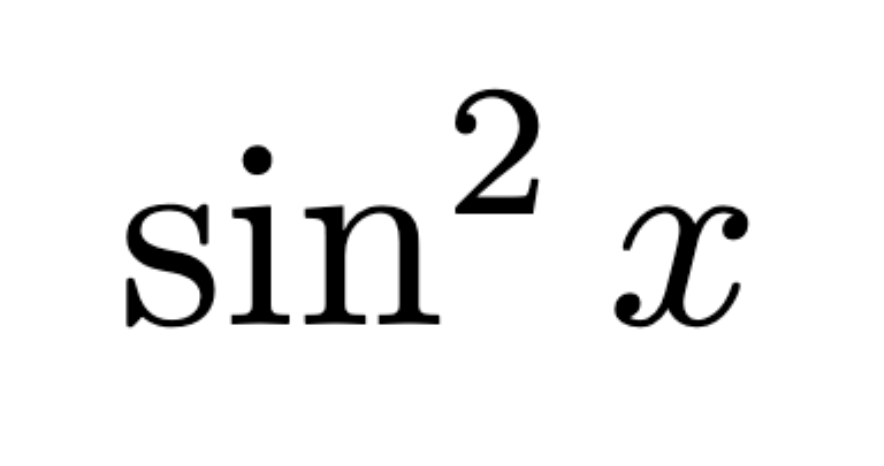
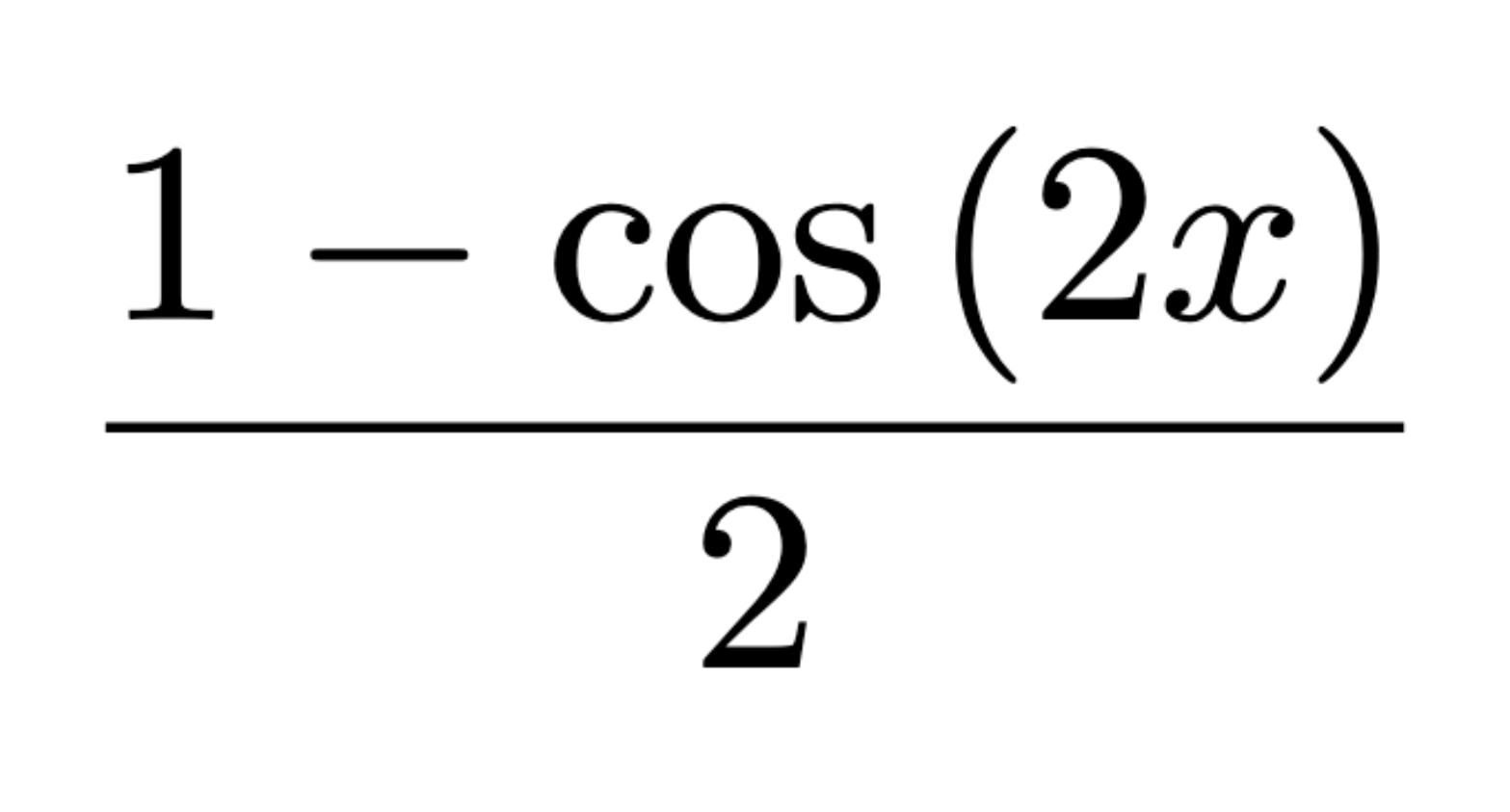
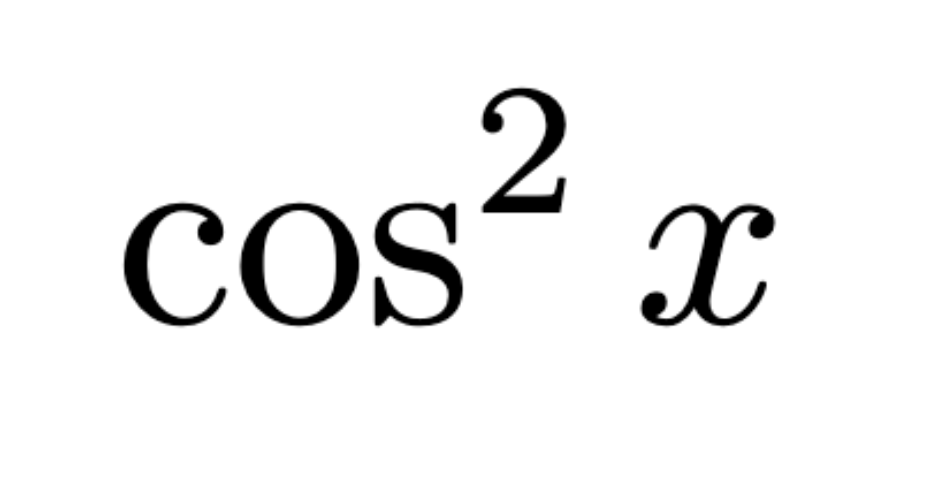
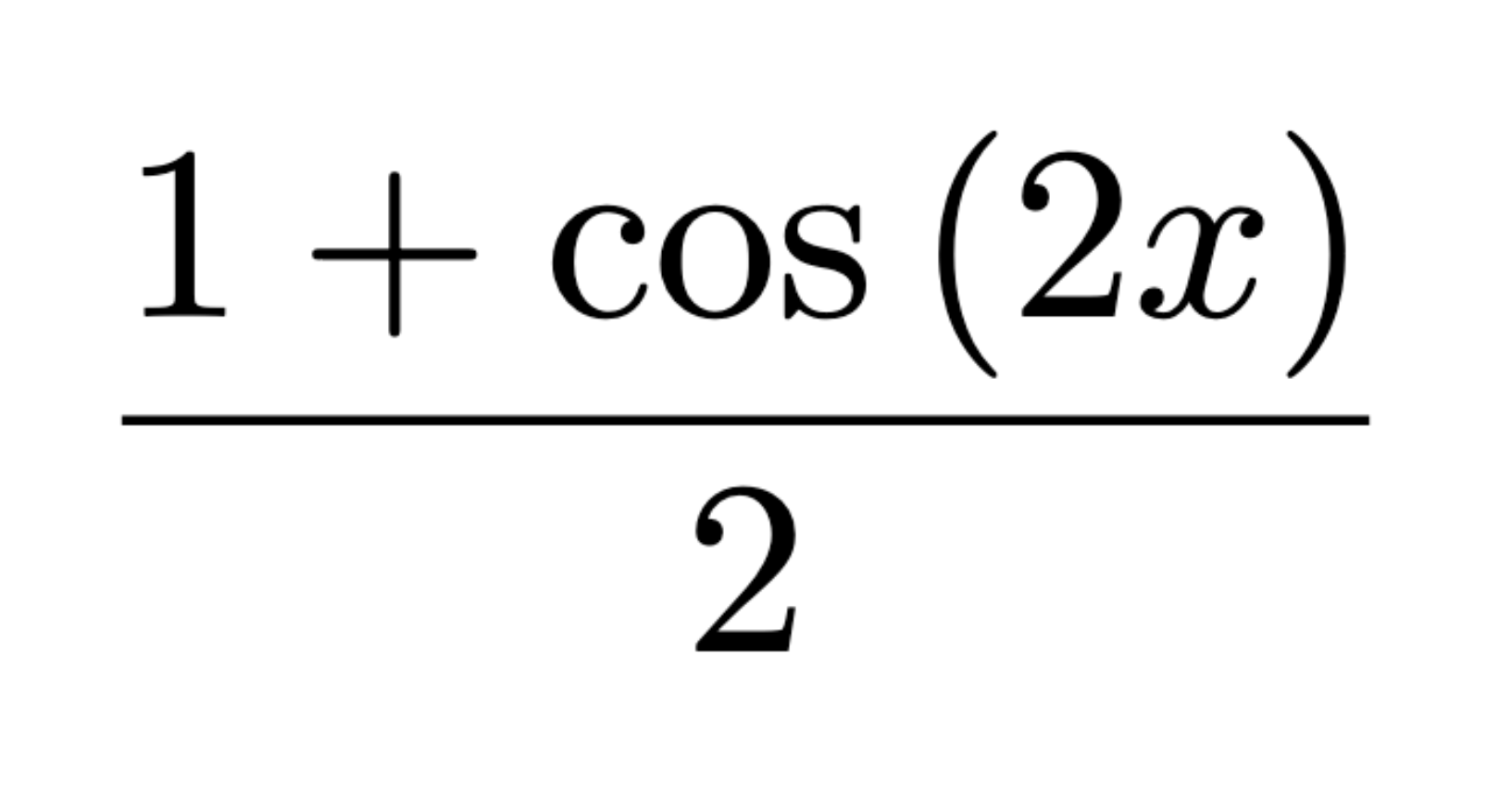
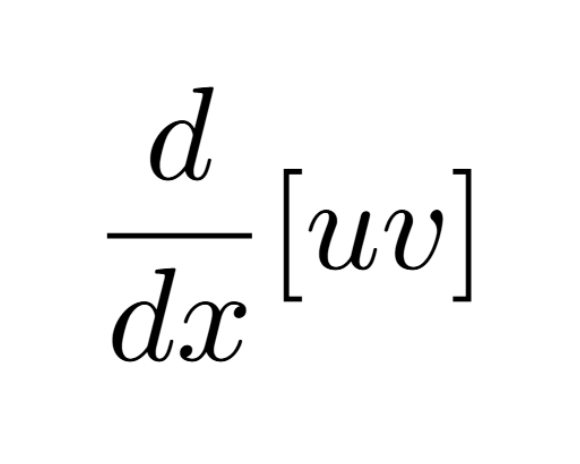
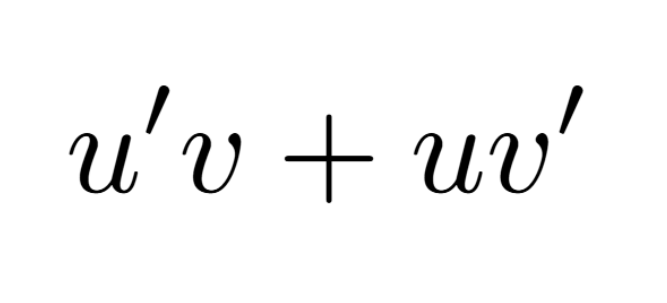
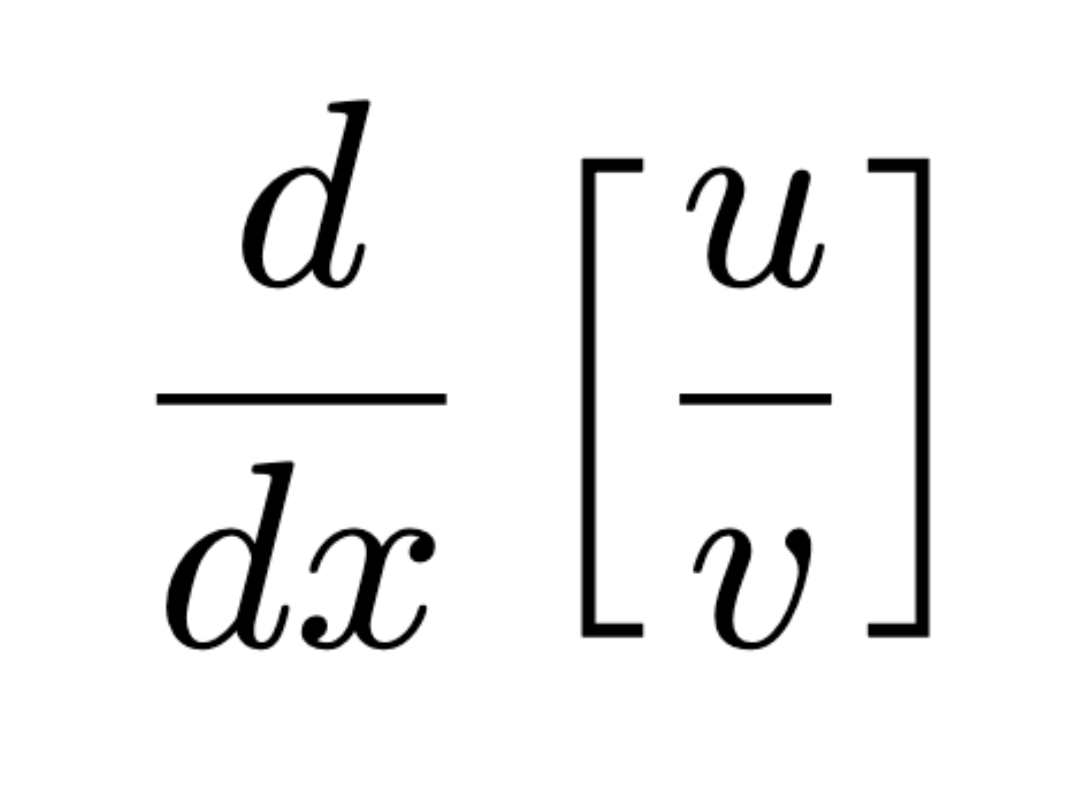
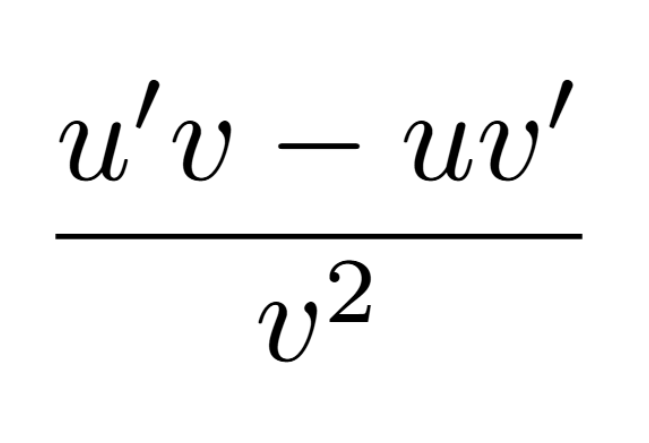
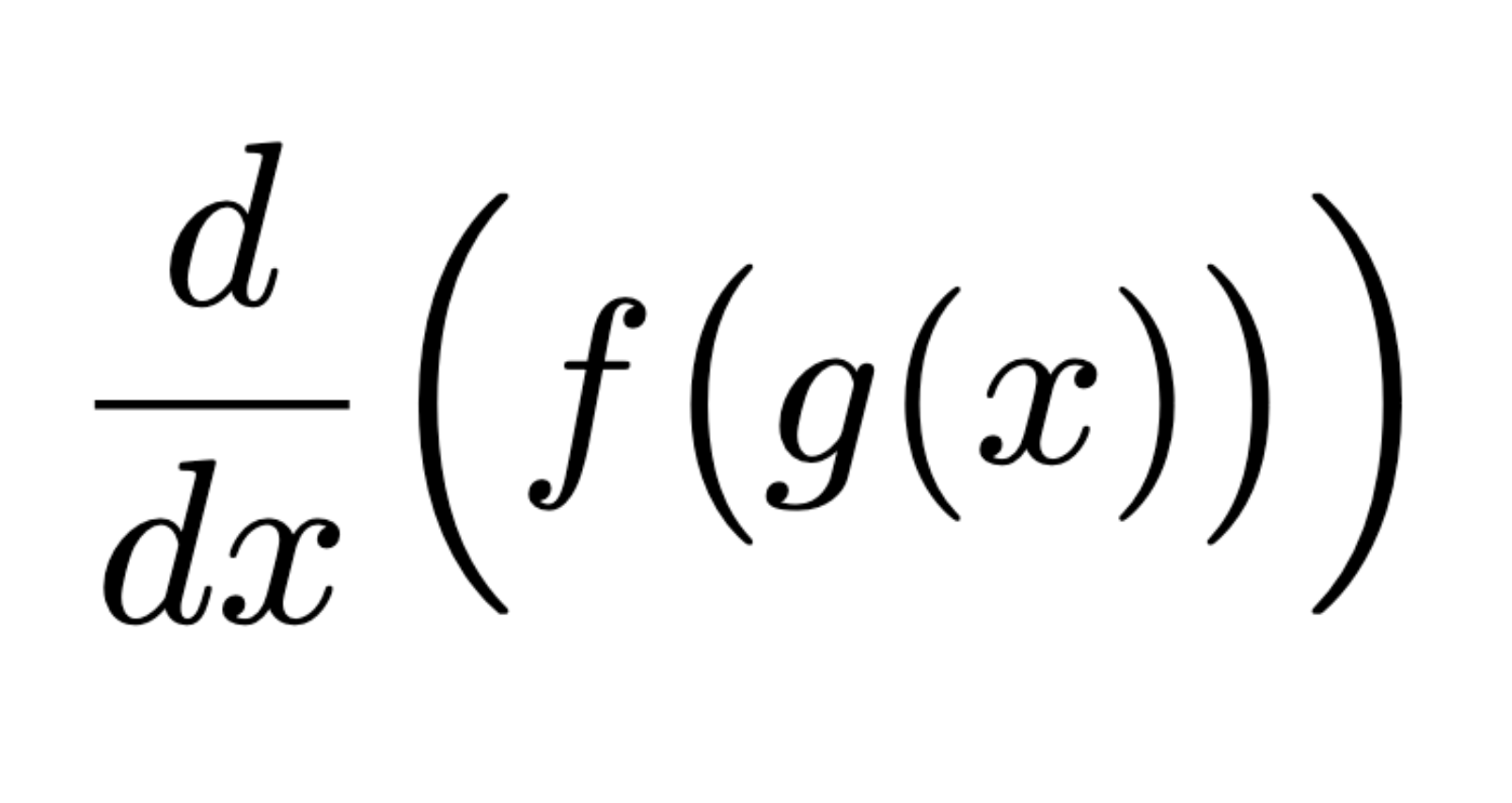
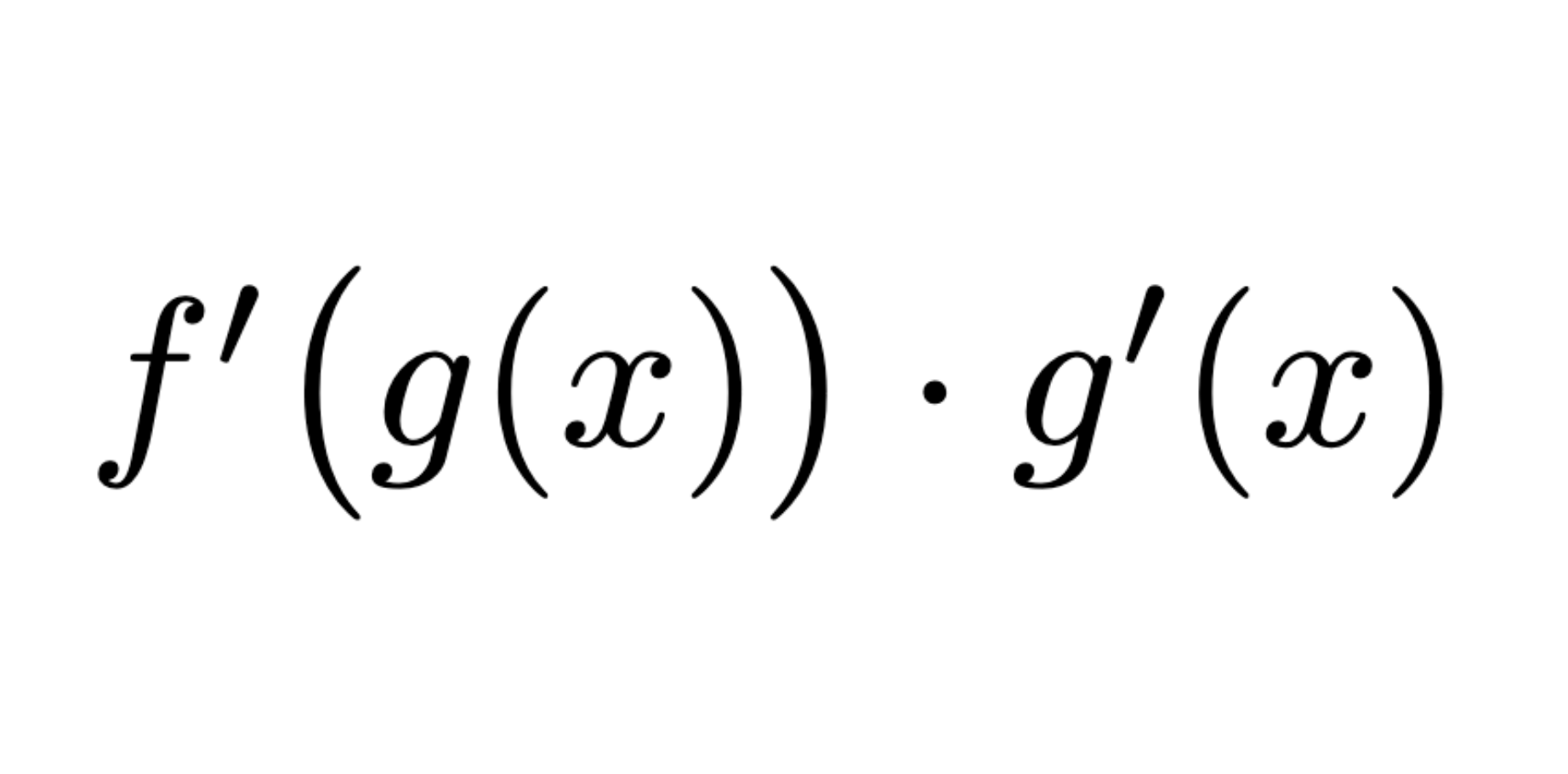
Extreme Value Theorem

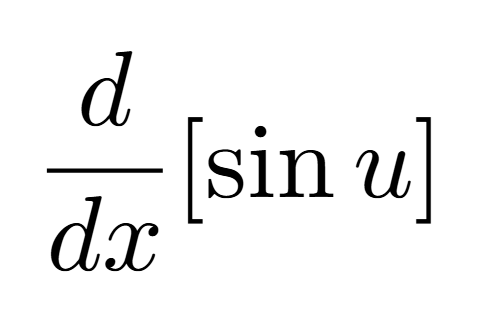
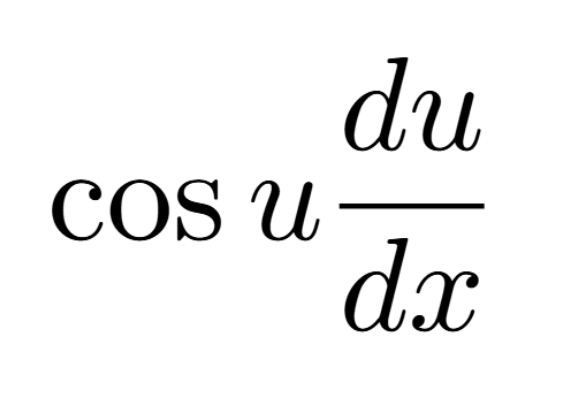
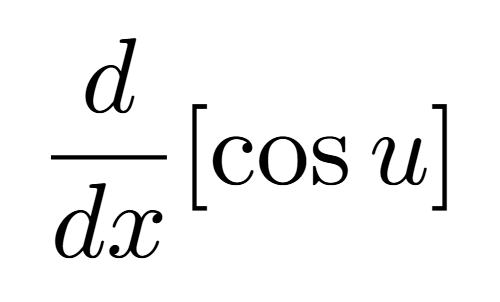
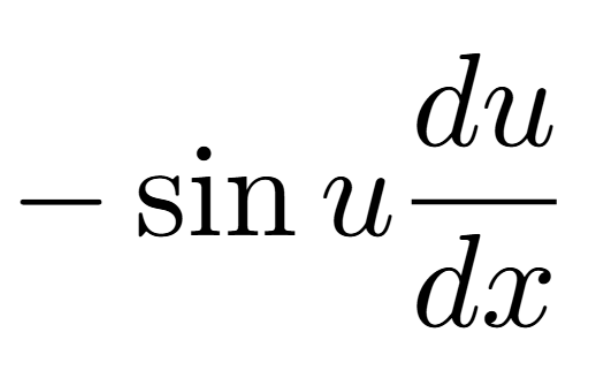
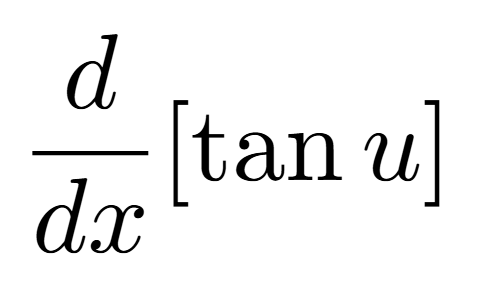
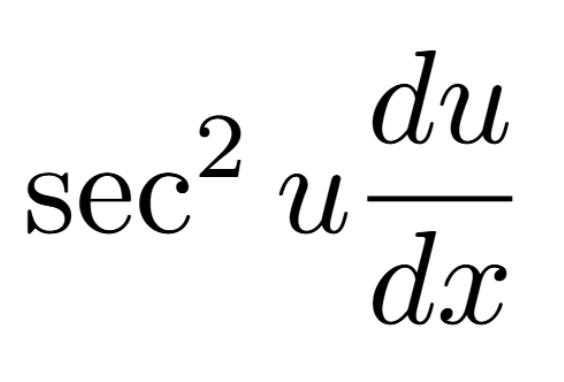

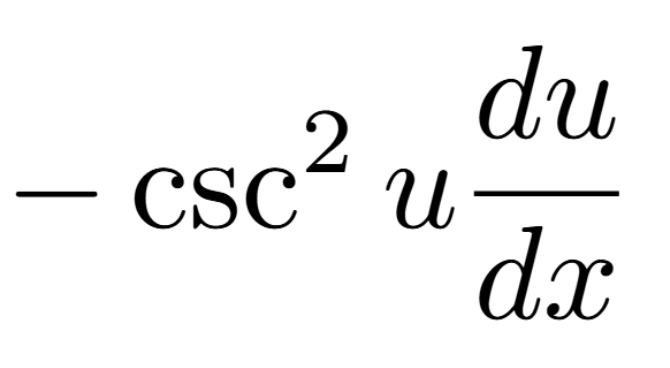
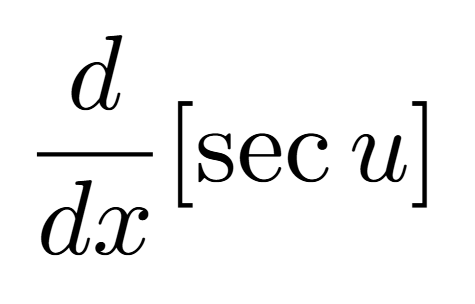
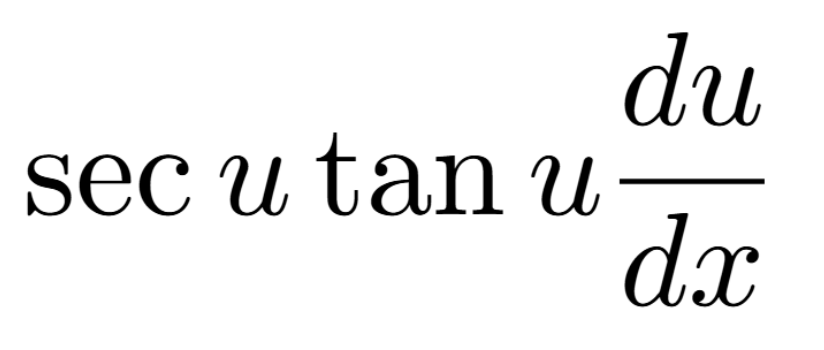
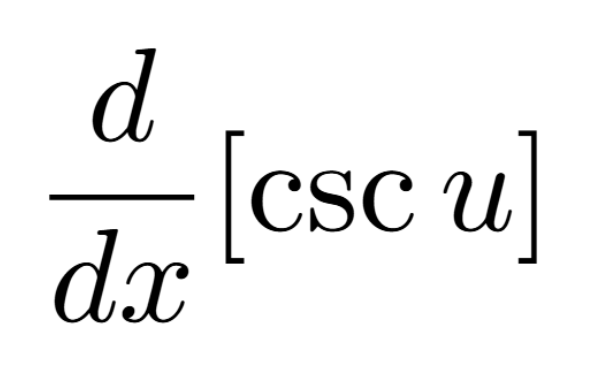
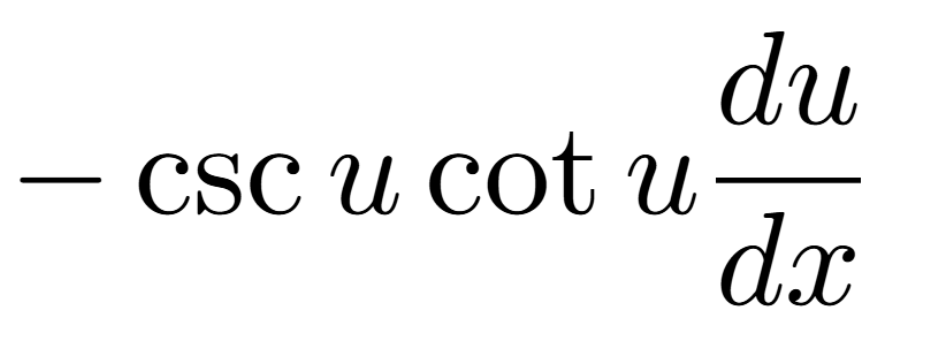
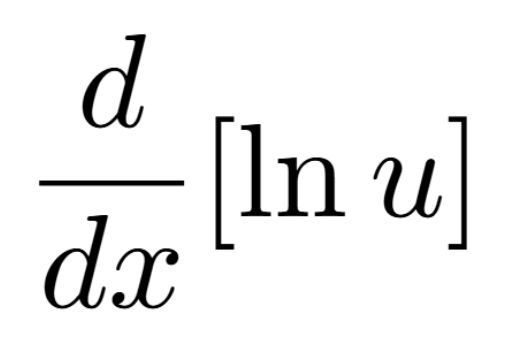
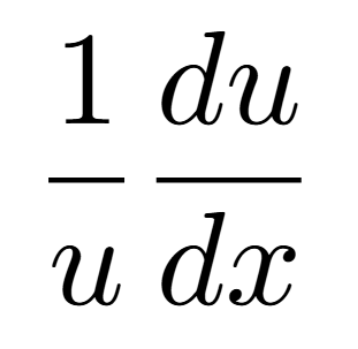
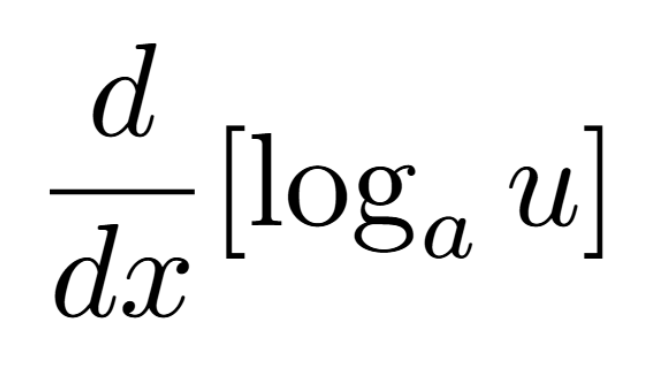
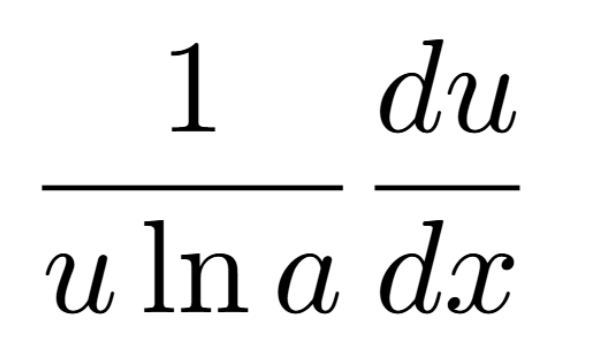
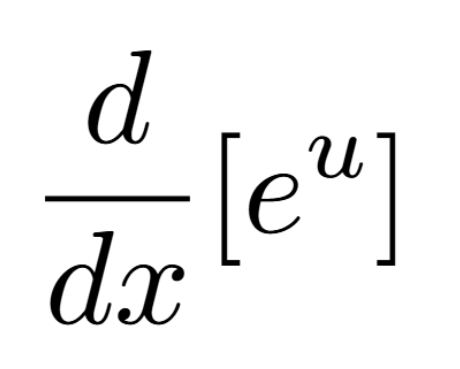
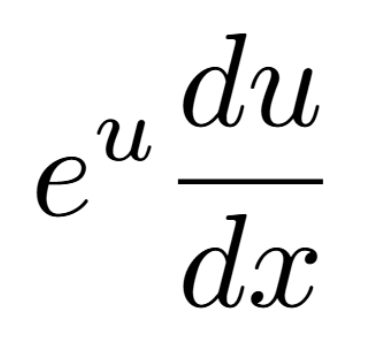
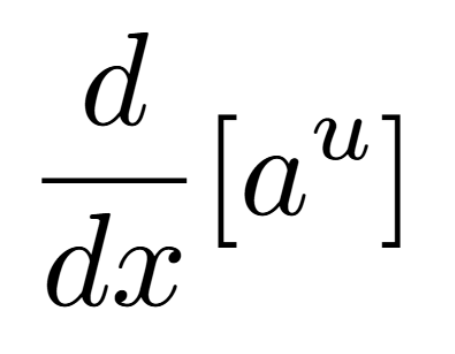
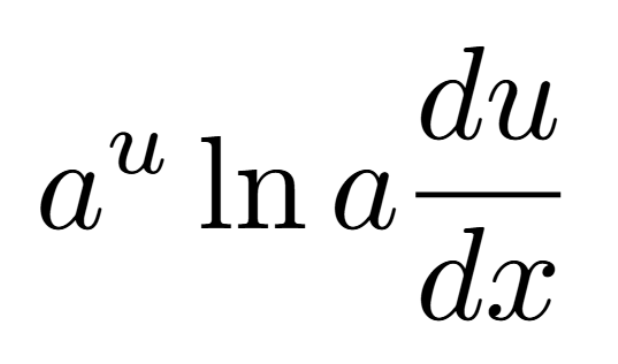

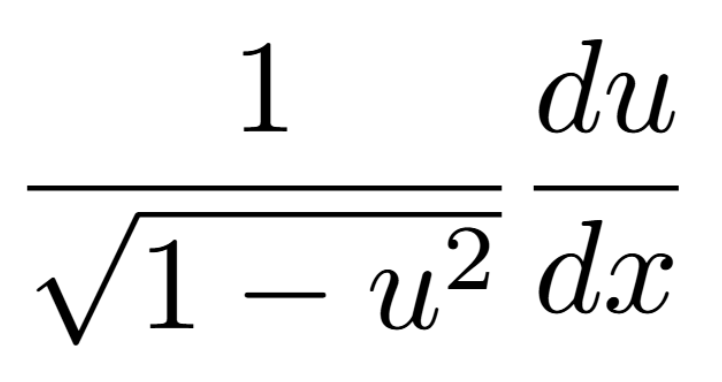
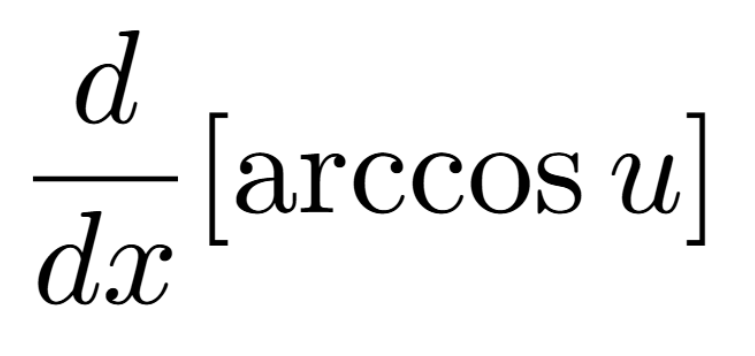
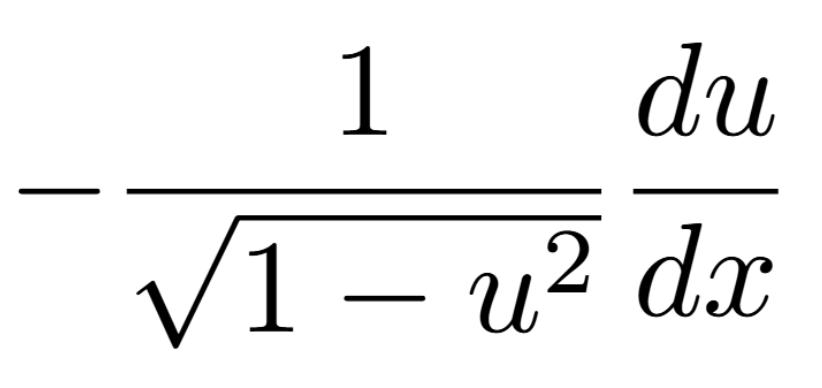

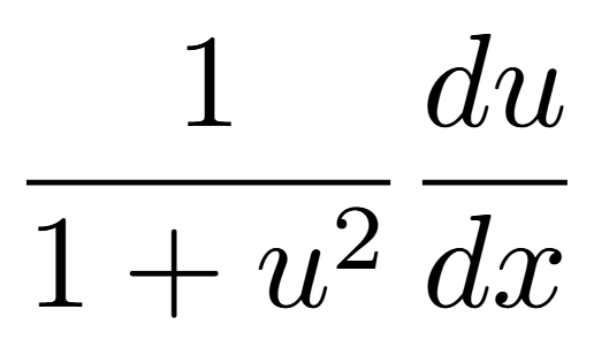
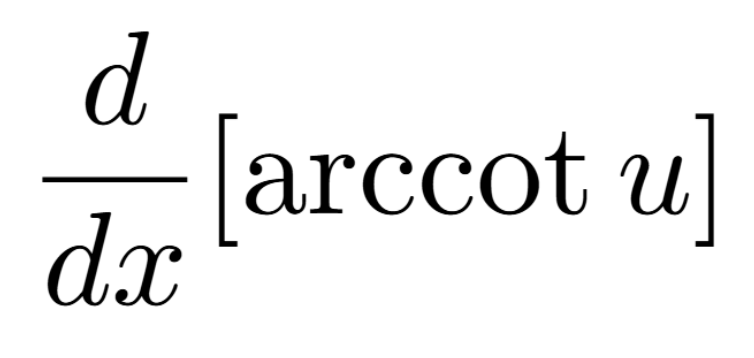
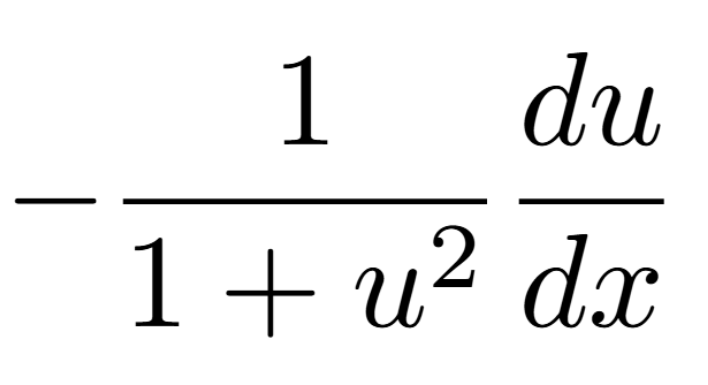
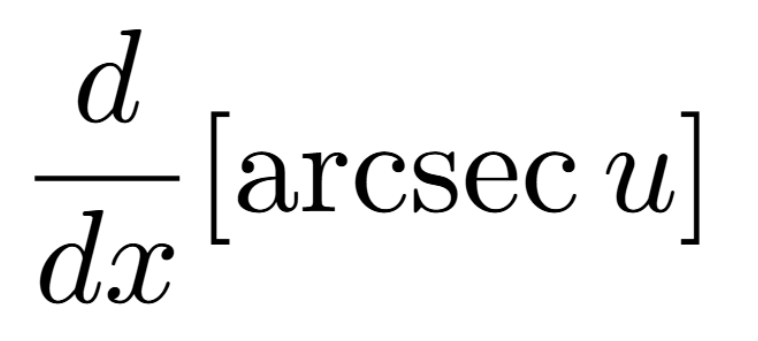
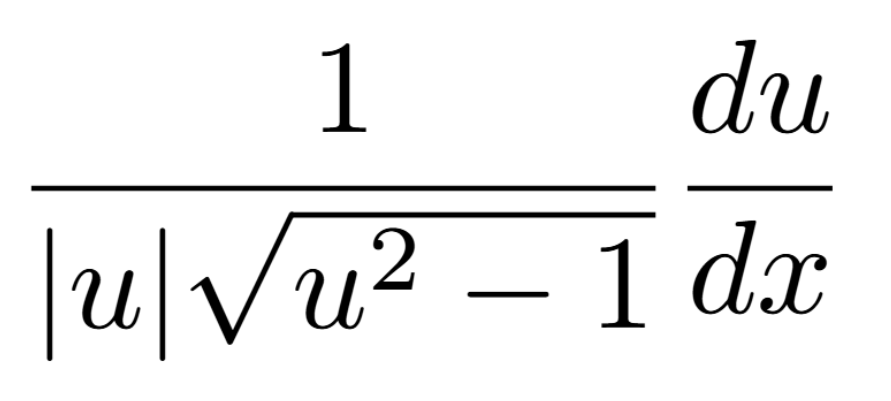
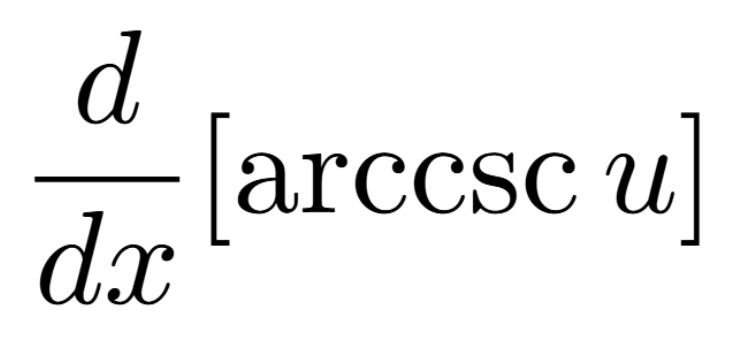
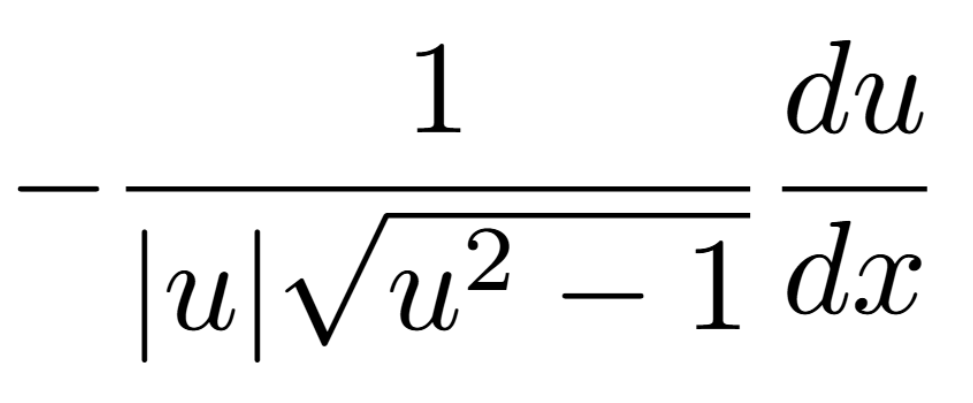
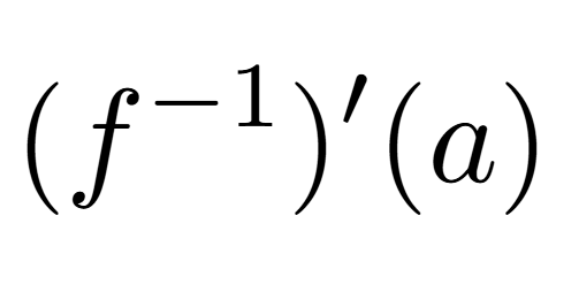
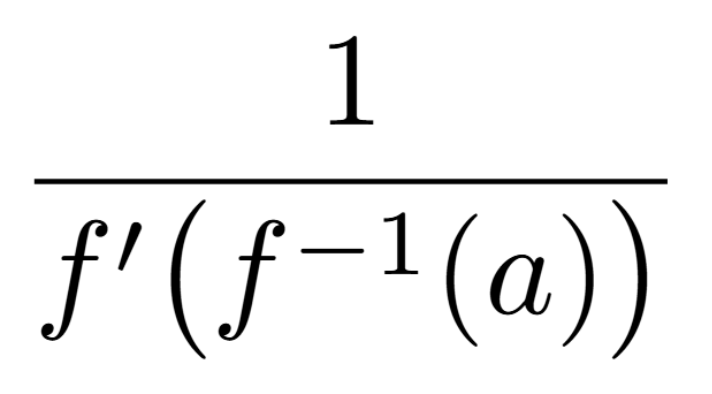
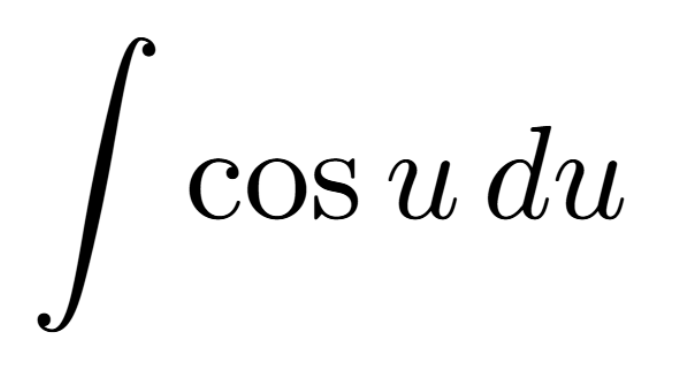
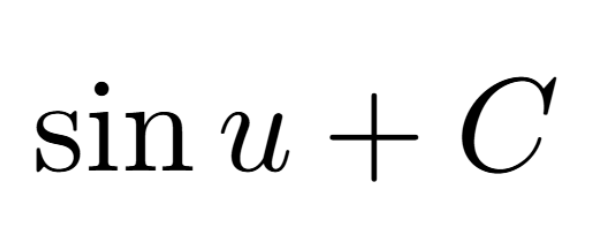
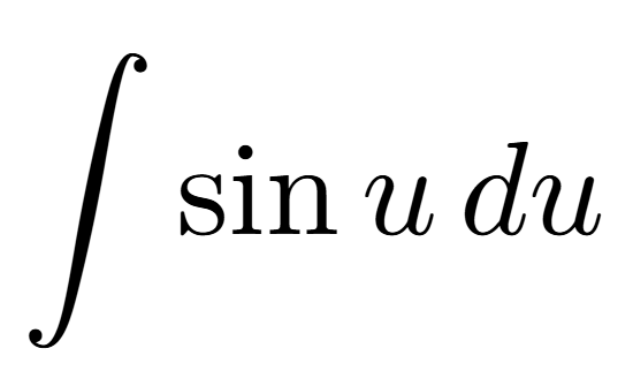
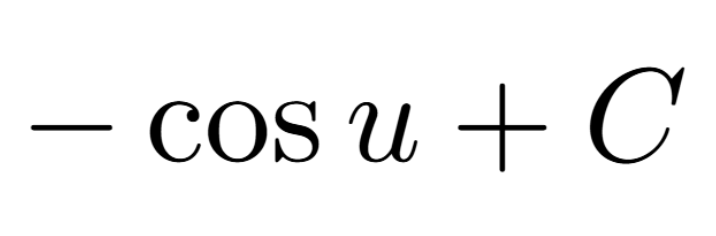
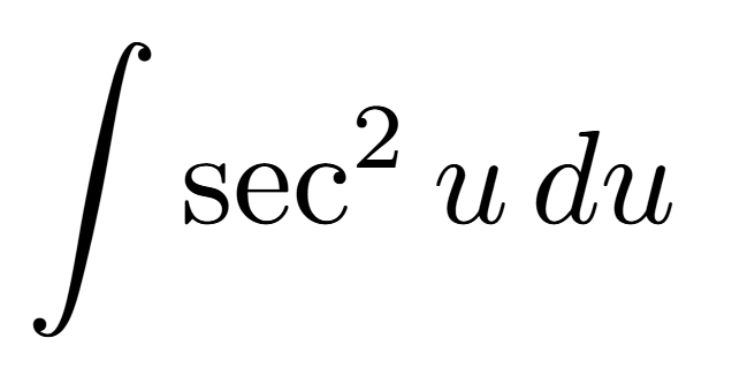
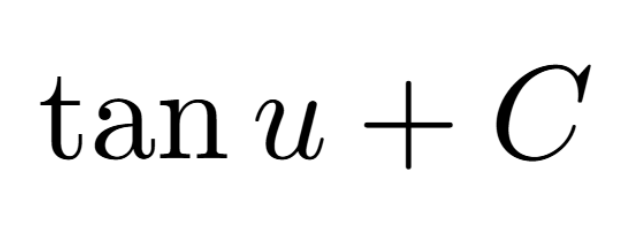
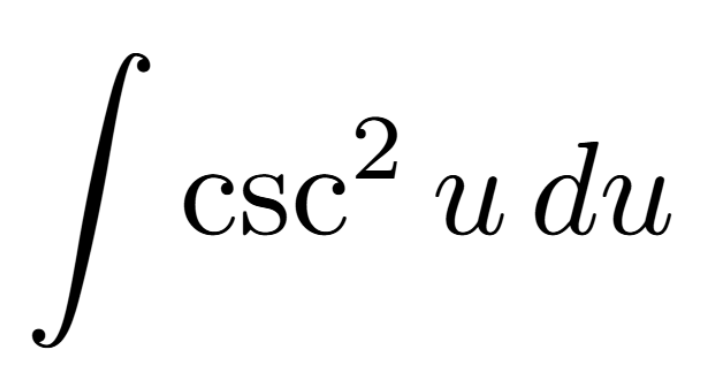
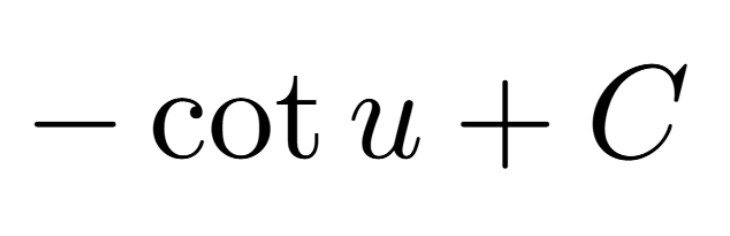
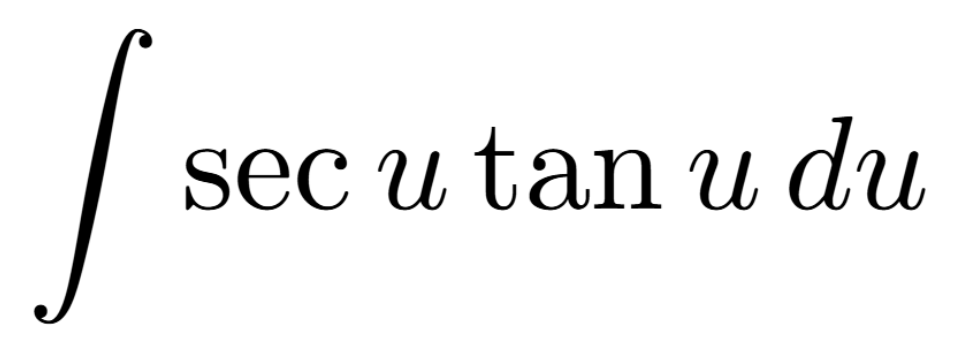
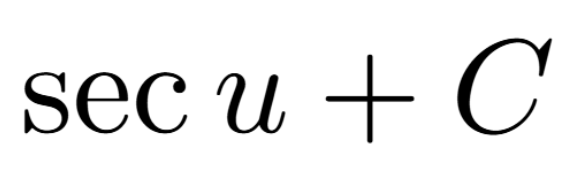
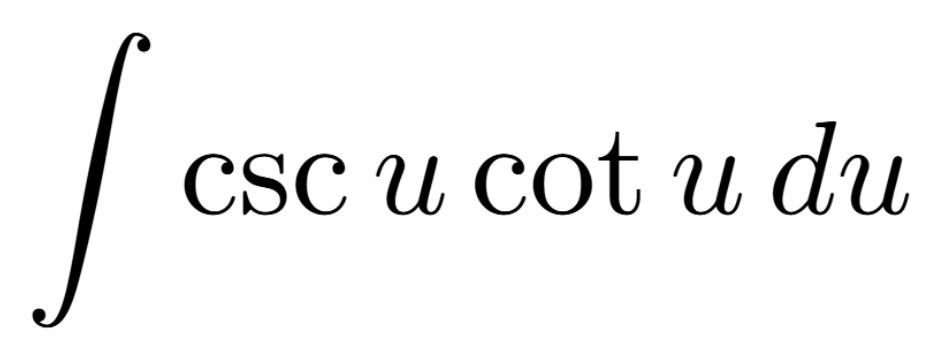
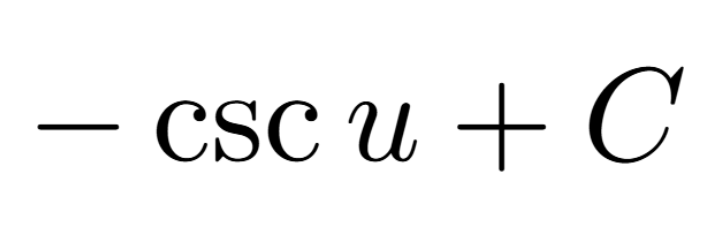
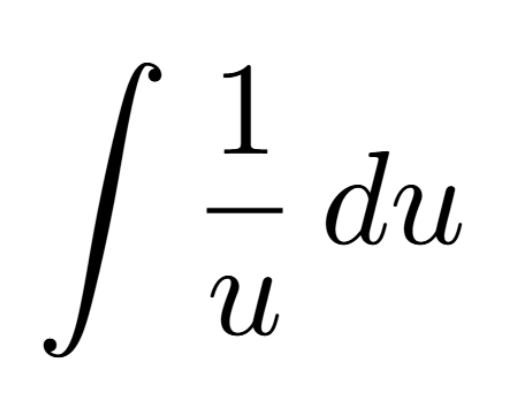
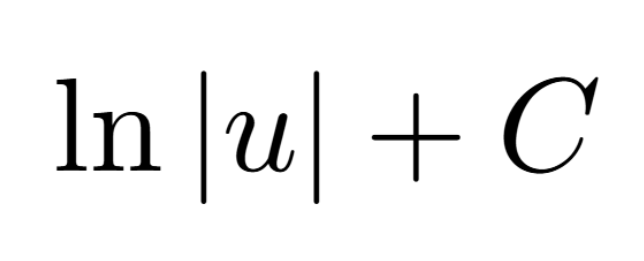
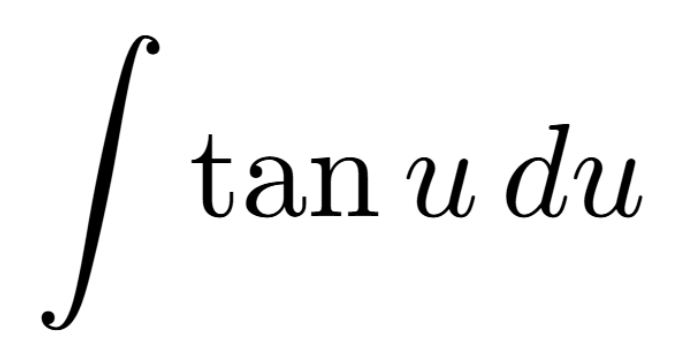
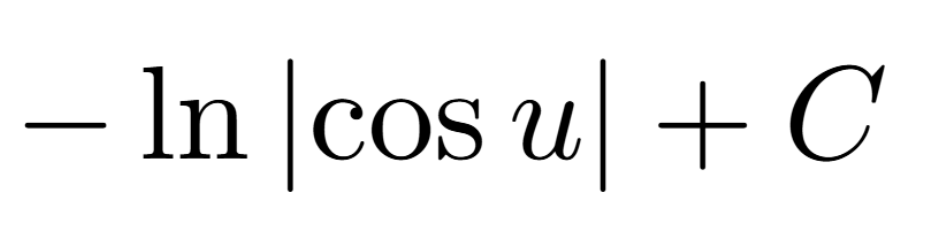
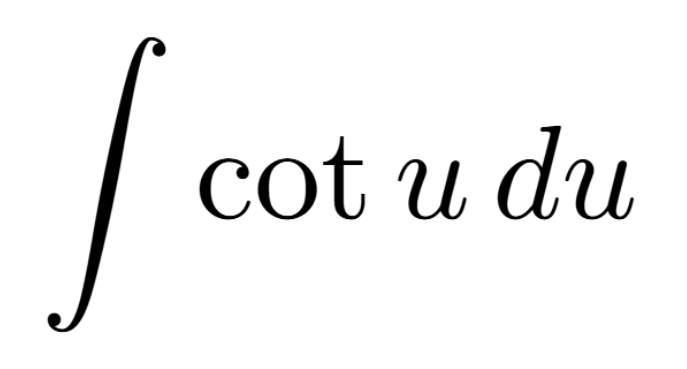
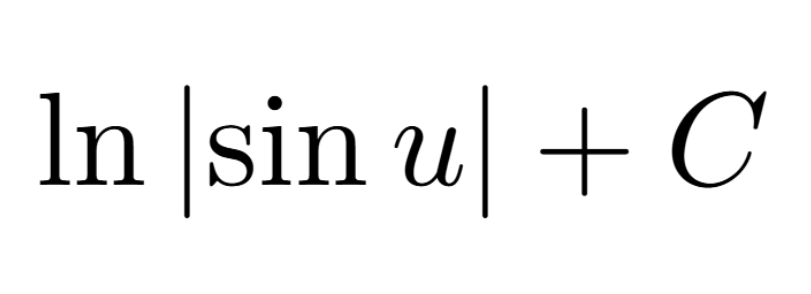
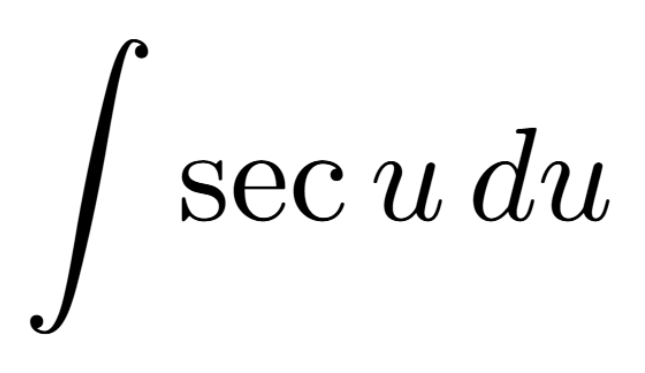
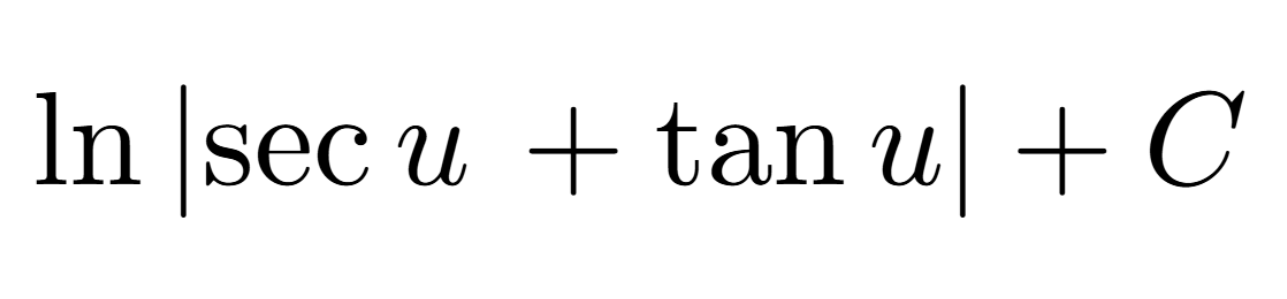
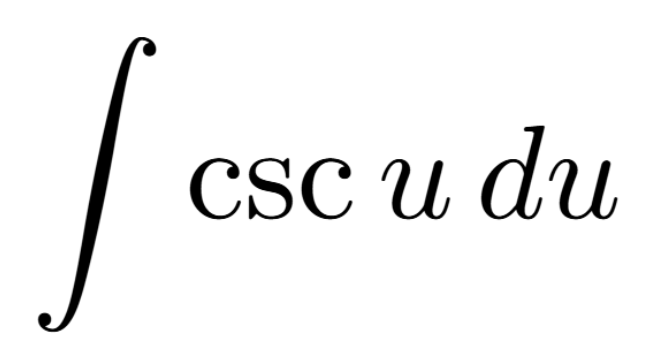
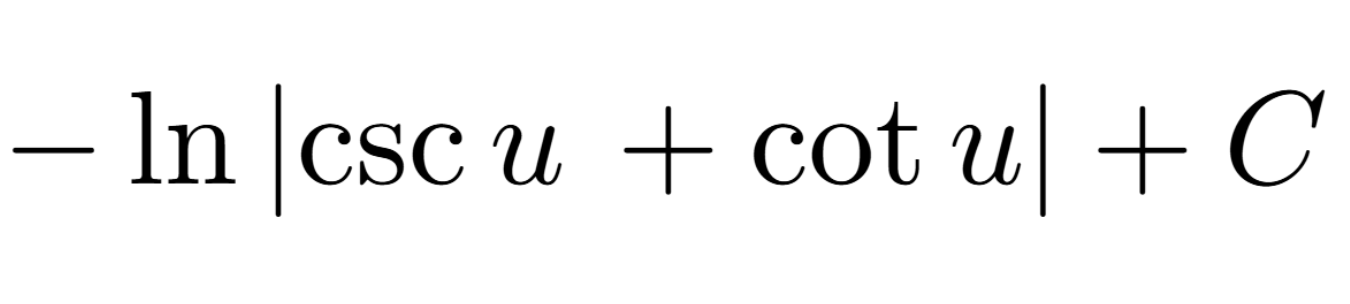
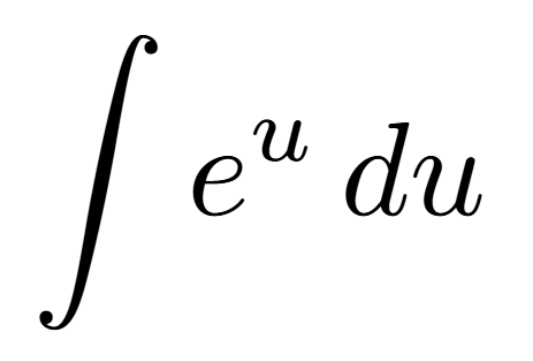
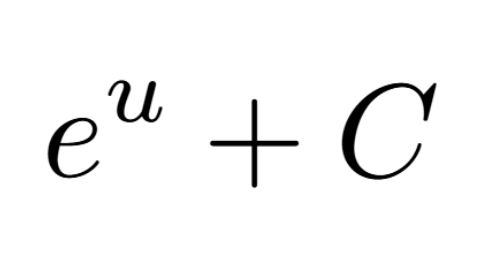
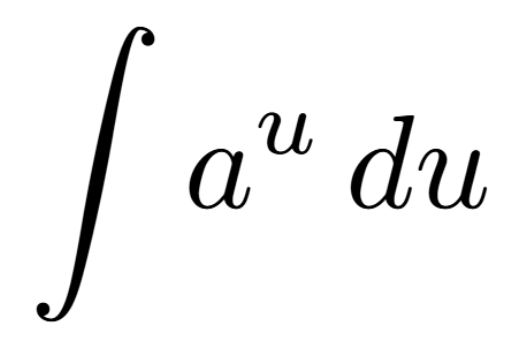
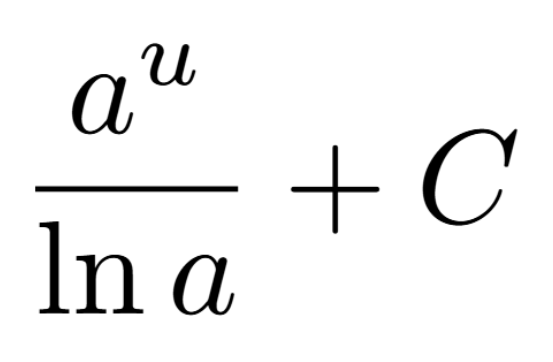
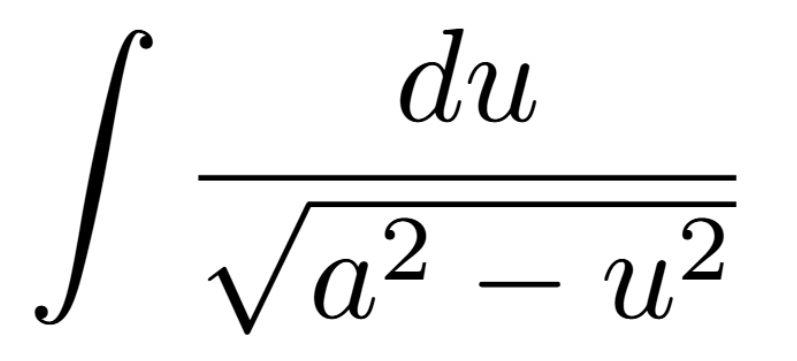
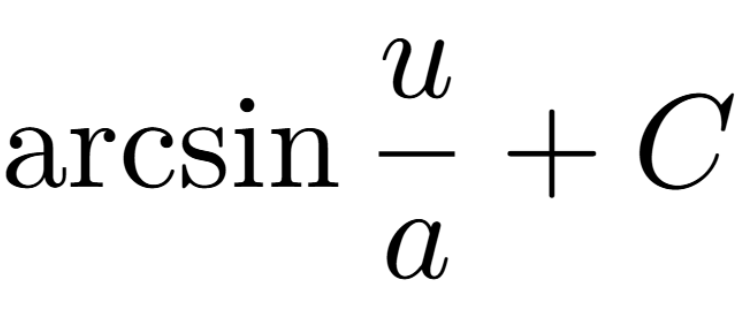

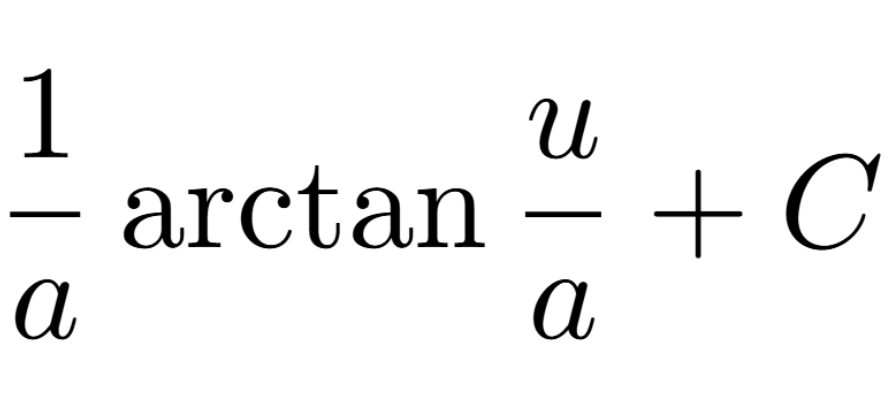
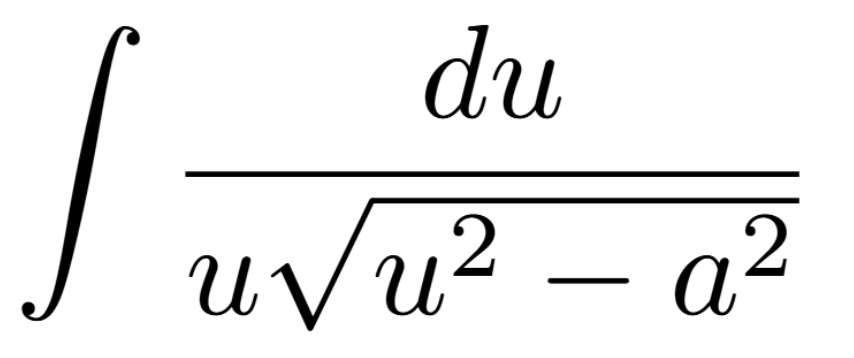
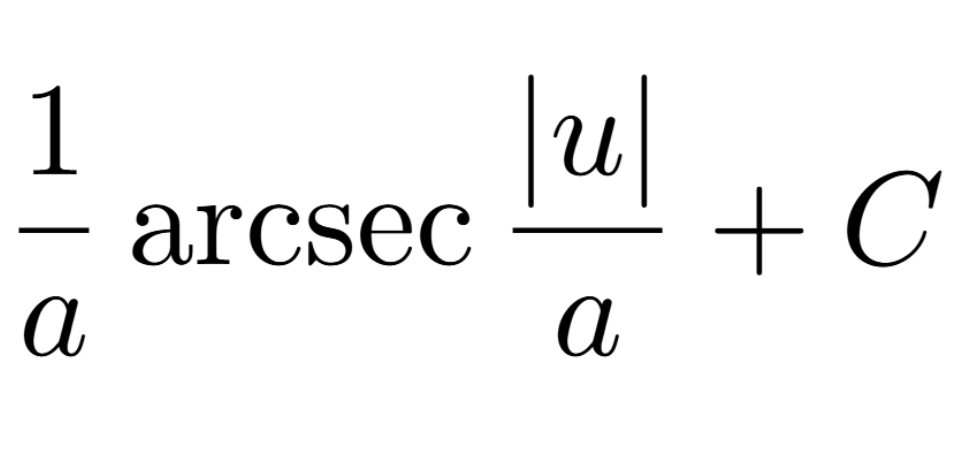
Definition of a Critical Number
Let f be defined at c. If f’(c) = 0 or if f’ is
undefined at c, then c is a critical number of f.
First Derivative Test
Let c be a critical number of a function f that is continuous on an
open interval I containing c. If f is differentiable on the interval,
except possibly at c, then f(c) can be classified as follows.
1) If f'(x) changes from negative to positive at c, then f(c) is a
relative minimum of f.
2) If f'(x) changes from positive to negative at c, then f(c) is a
relative maximum of f.
Second Derivative Test
Let f be a function such that f’(c) = 0 and the second
derivative of f exists on an open interval containing c.
1) If f’’(c) > 0, then f(c) is a relative minimum.
2) If f’’(c) < 0, then f(c) is a relative maximum.
Definition of Concavity
Let f be differentiable on an open interval I. The graph of f
is concave upward on I if f’ is increasing on the interval and
concave downward on I if f′ is decreasing on the interval.
Test for Concavity
Let f be a function whose second derivative exists on an open interval I.
1) If f’’(x) > 0 for all x in I, then the graph of f is concave upward in I.
2) If f’’(x) < 0 for all x in I, then the graph of f is concave downward in I.
Definition of an Inflection Point
A function f has an inflection point at (c, f(c))
1) If f’’(c) = 0 or f’’(c) does not exist and
2) If f’’ changes sign at x = c or if f′ changes from
increasing to decreasing or vice versa at x = c.
Second Fundamental Theorem of Calculus
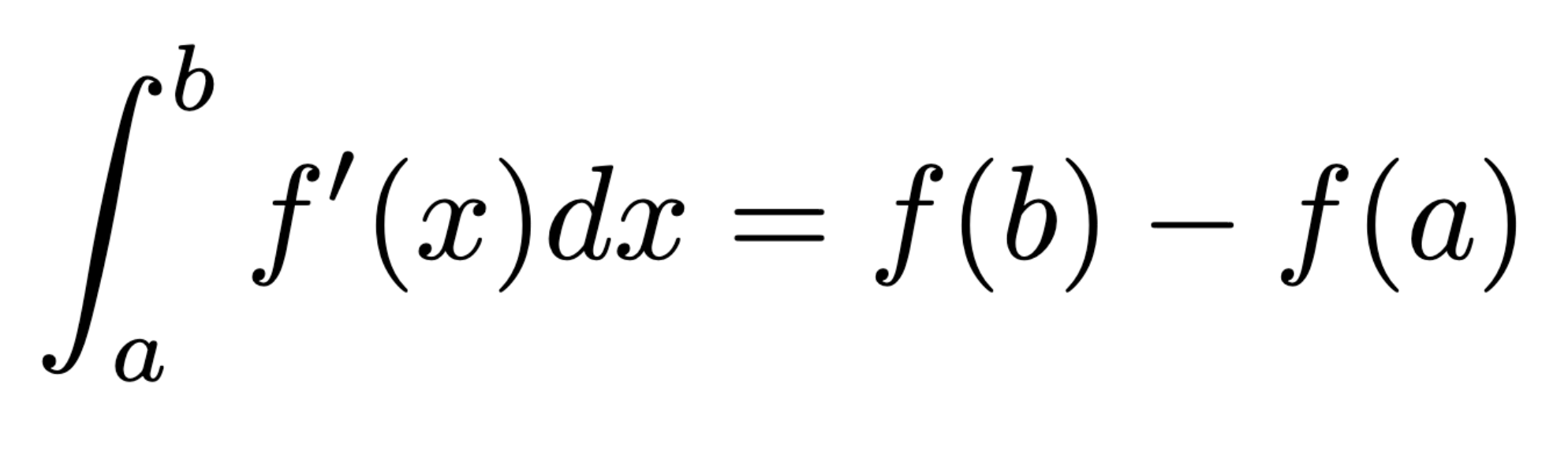
First Fundamental Theorem of Calculus
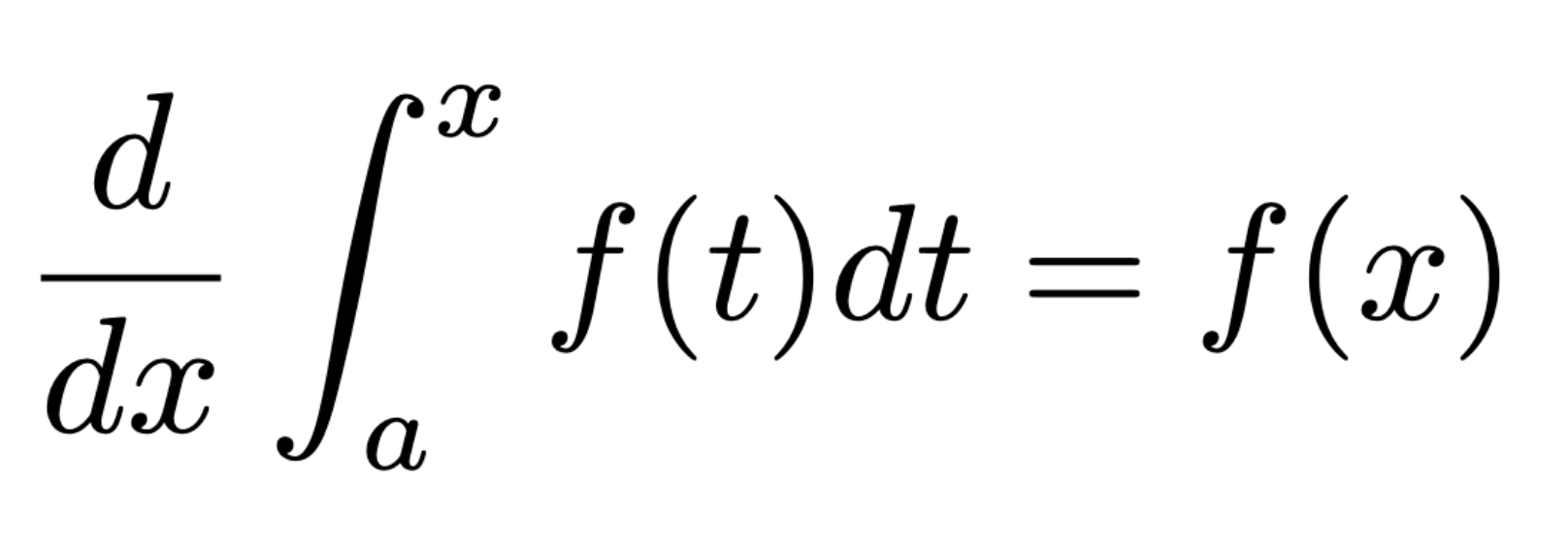
Chain Rule Version
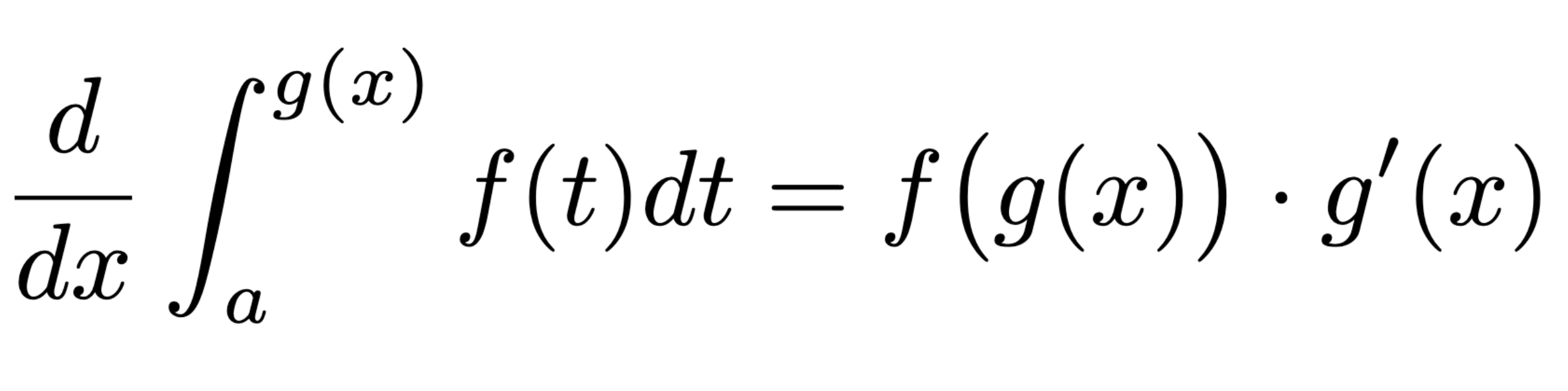
Volume around a horizontal axis by discs
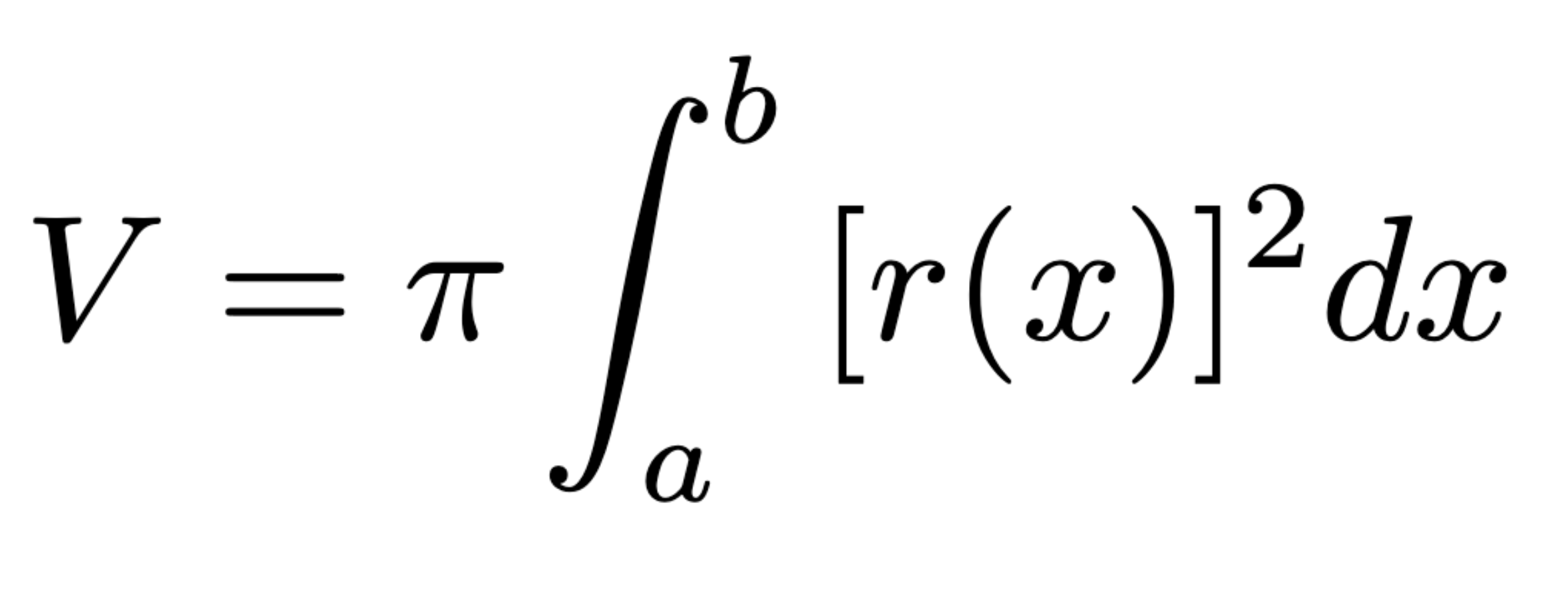
Volume around a horizontal axis by washers
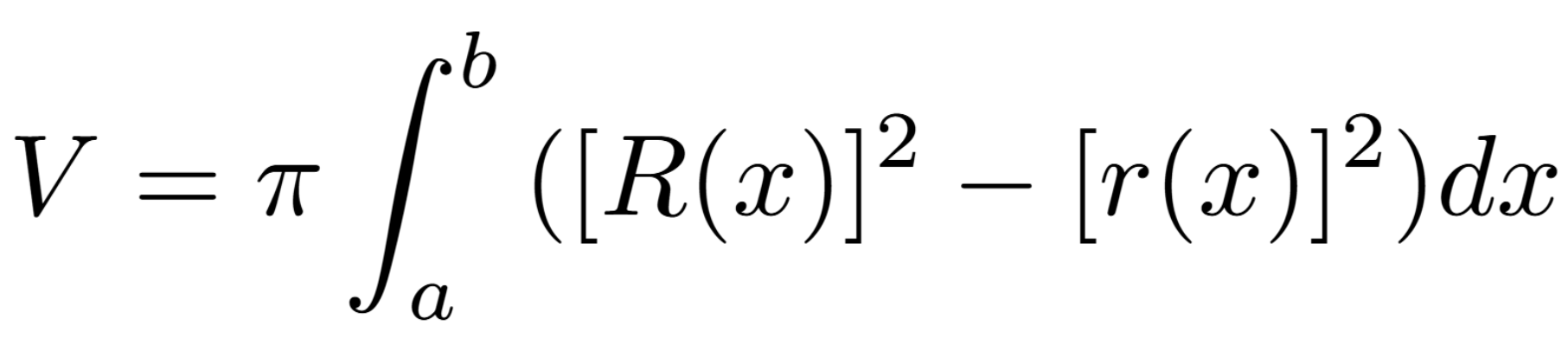
Volume by cross sections taken perpendicular to the x-axis
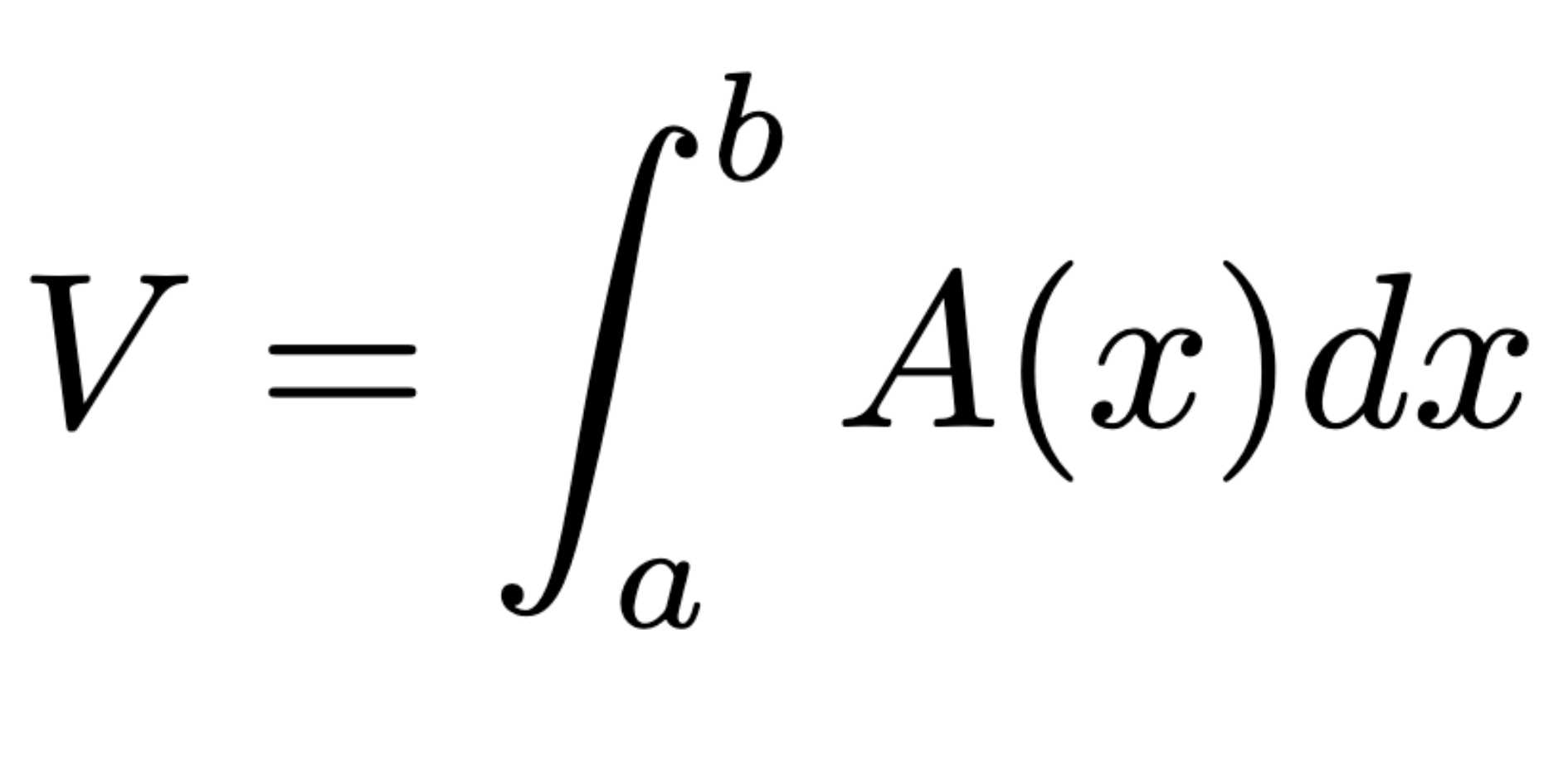
If an object moves along a straight line with
position function s(t), then its velocity is…
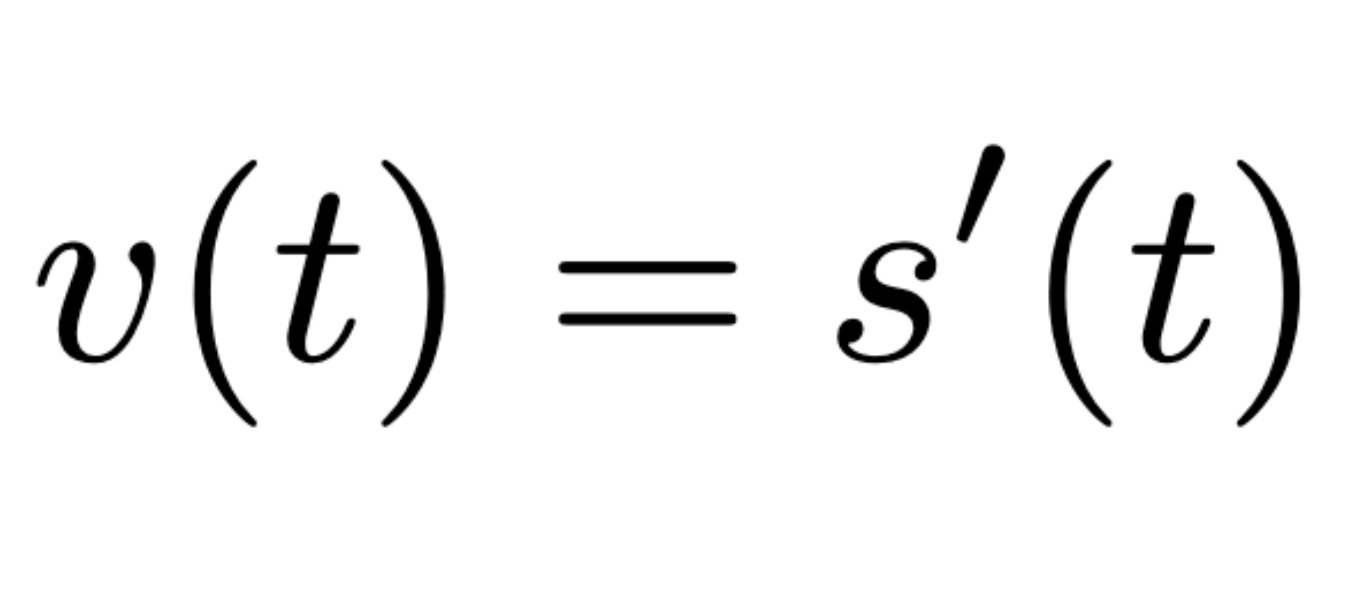
Speed
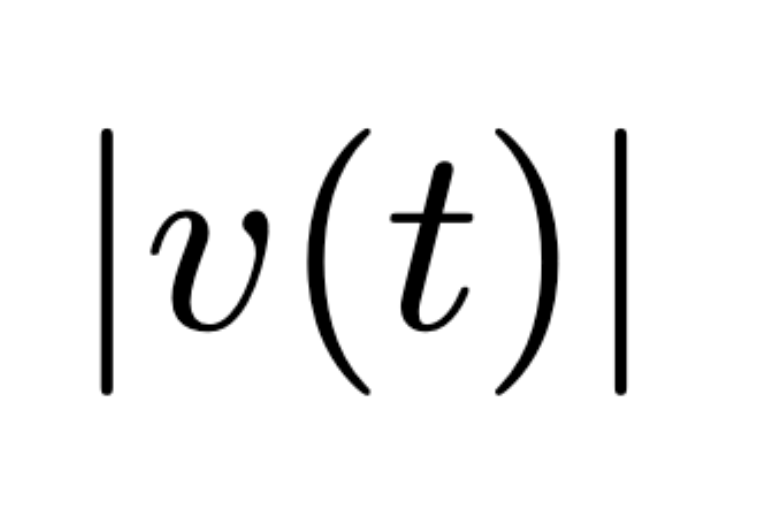
Acceleration
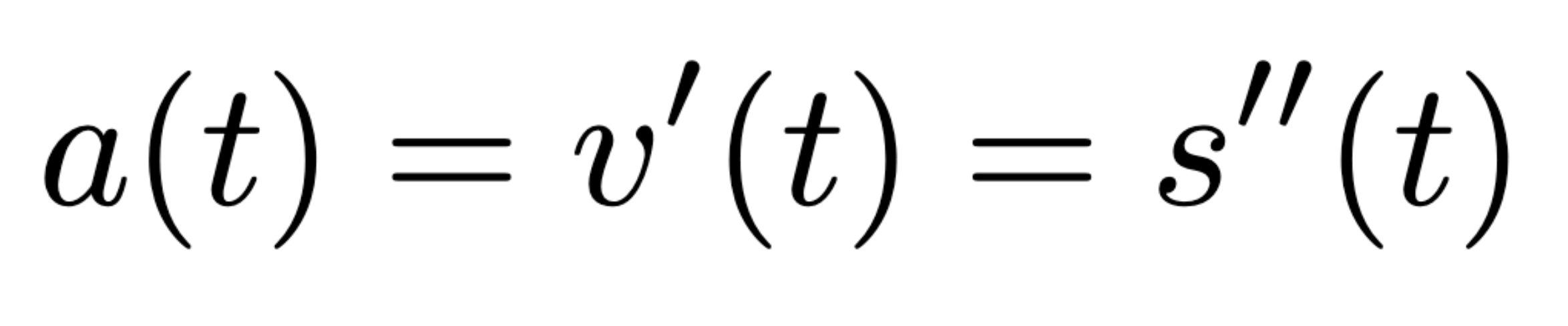
Displacement (change in position) from x = a to x = b
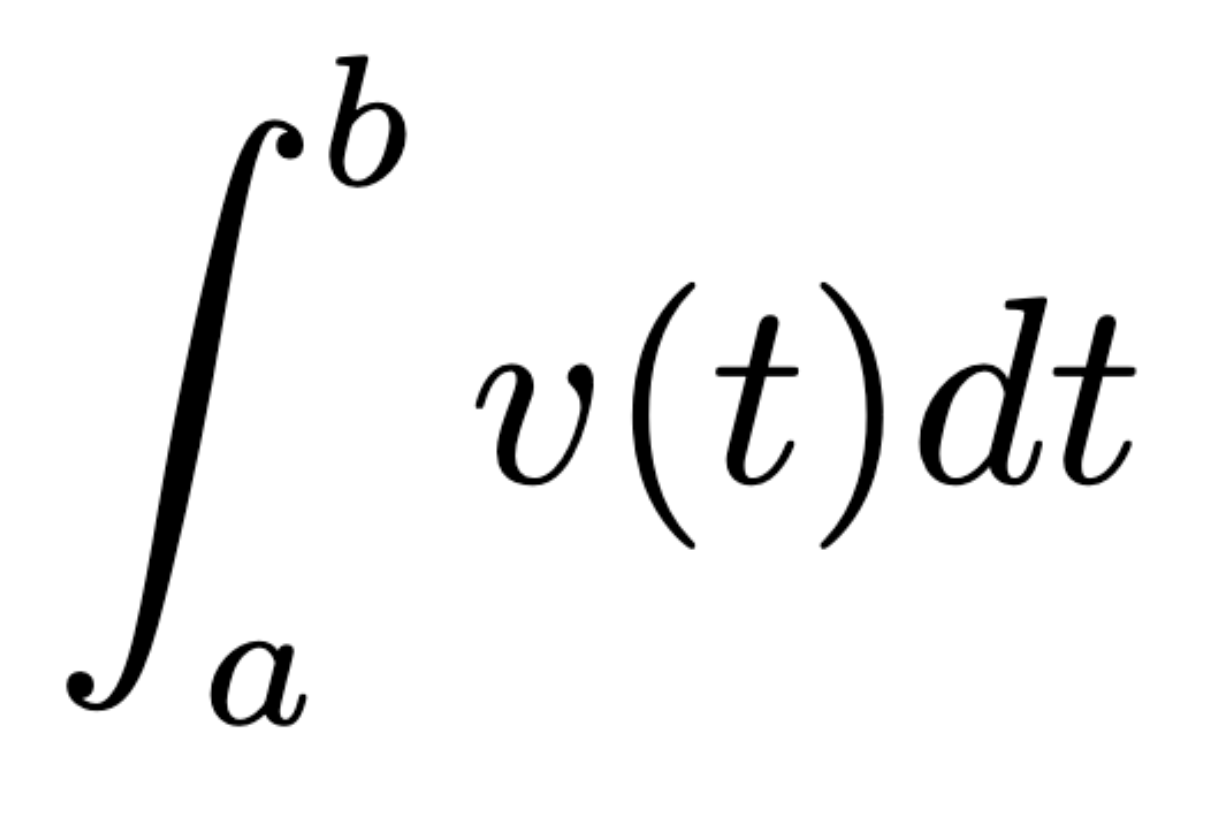
Total distance traveled from x = a to x = b
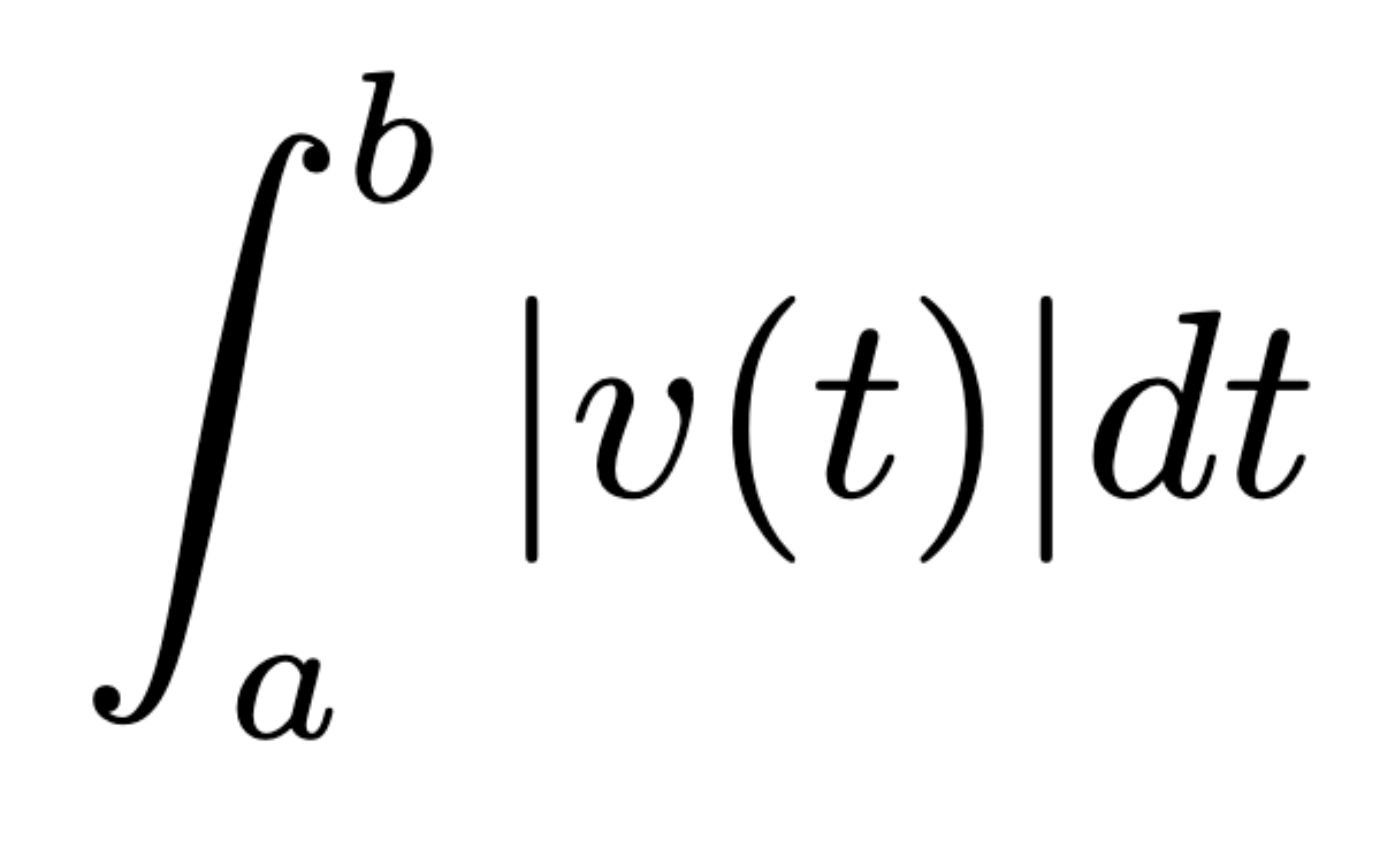
Total distance where v(t) changes sign at x = c
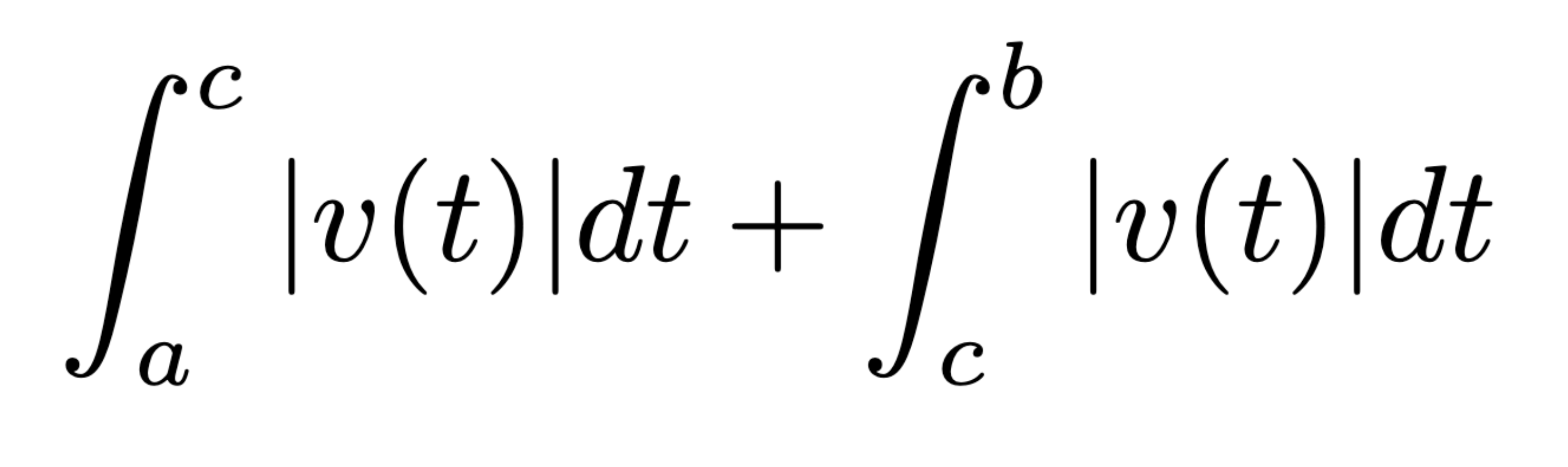
Integration by parts

Logistic growth
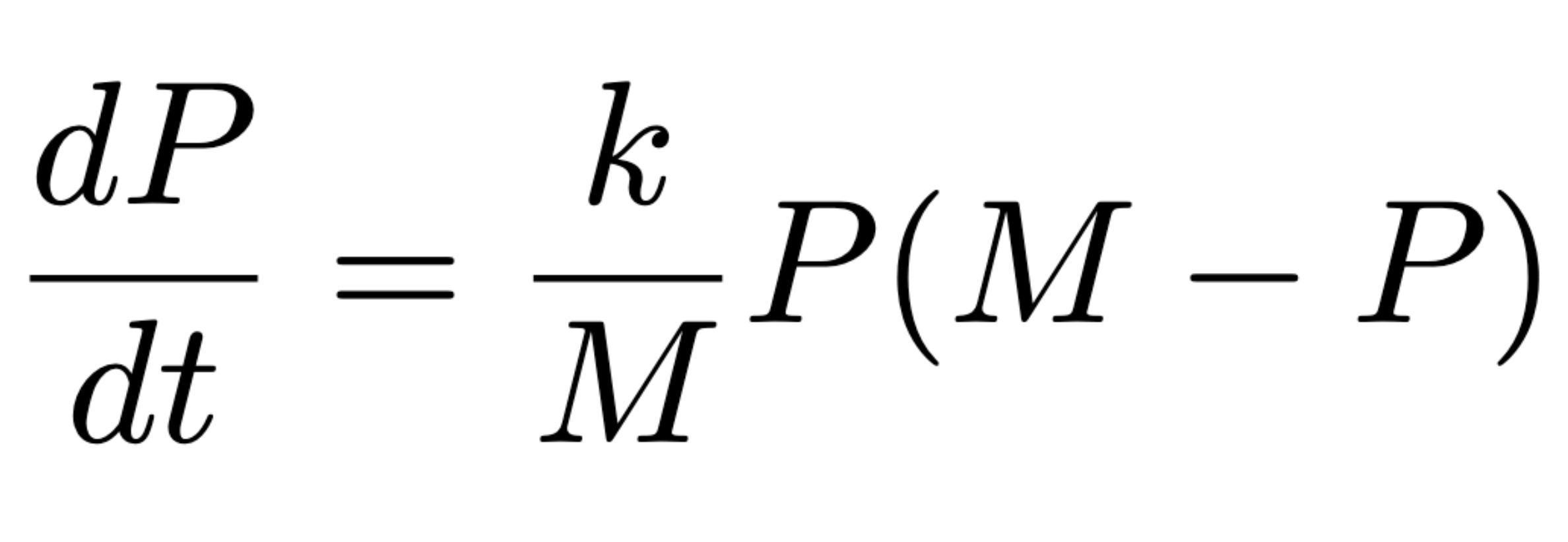
Length of arc for functions
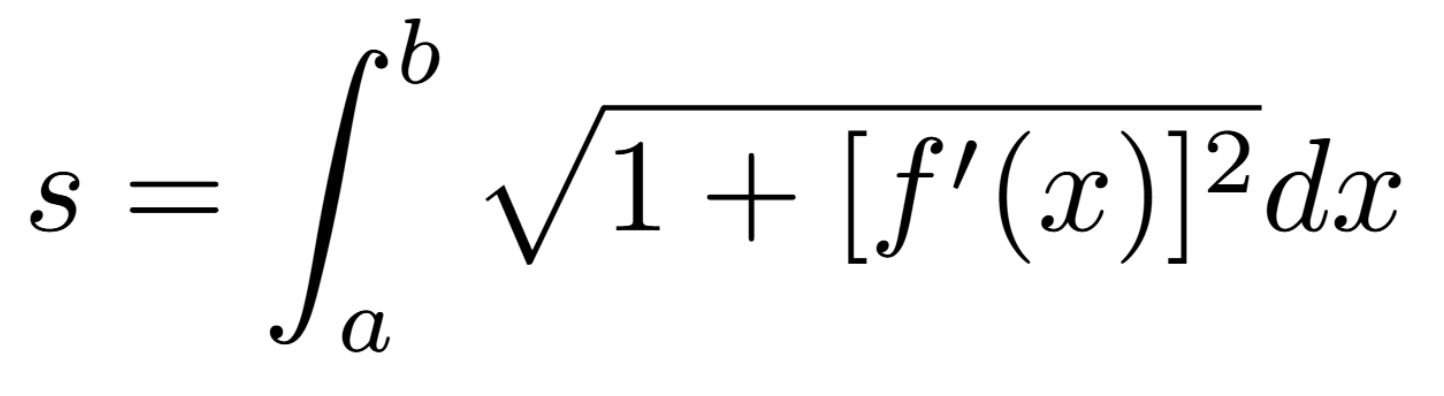
If an object moves along a curve, its position vector is…
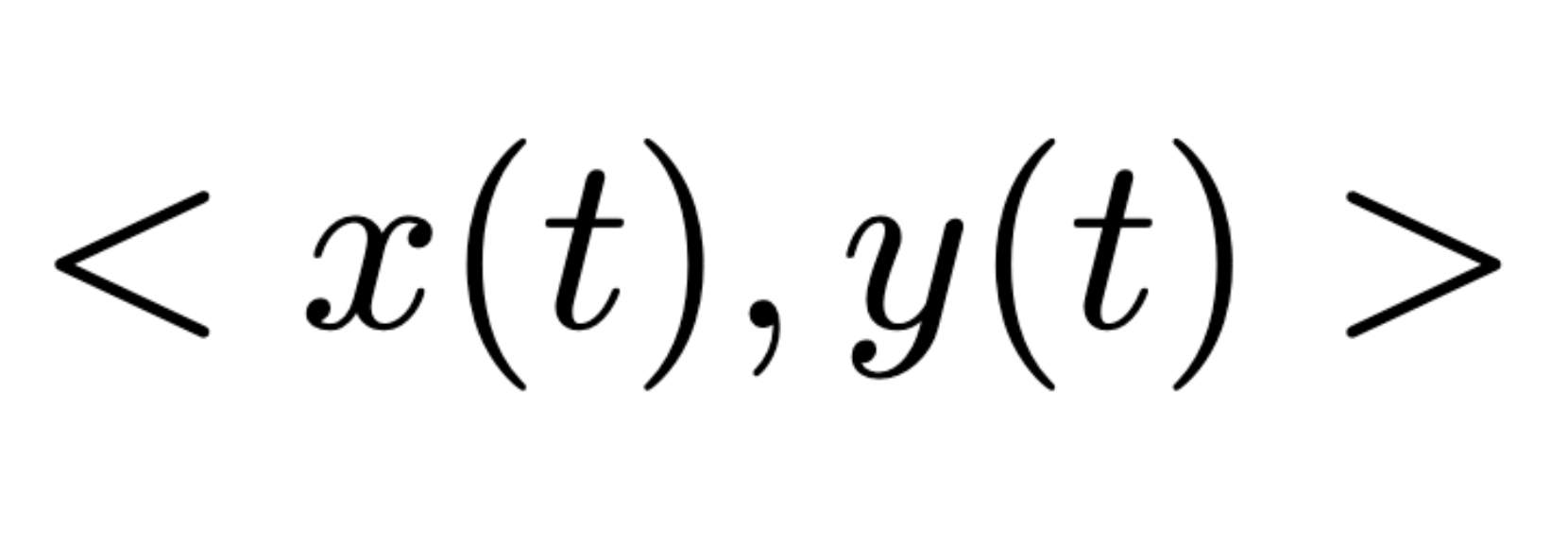
Velocity vector
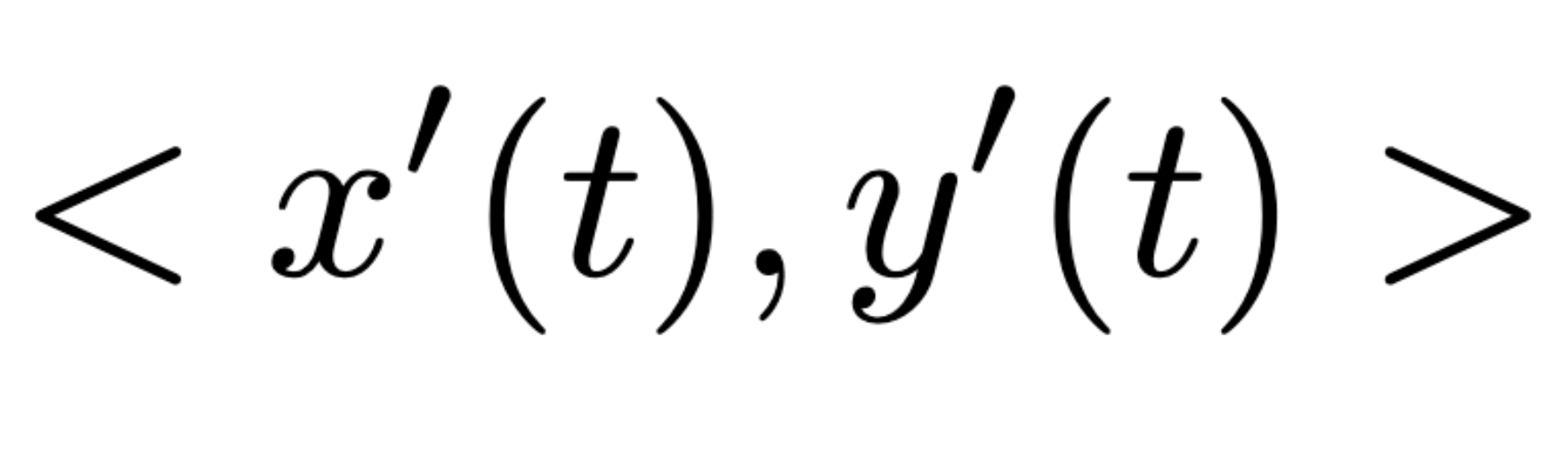
Acceleration vector
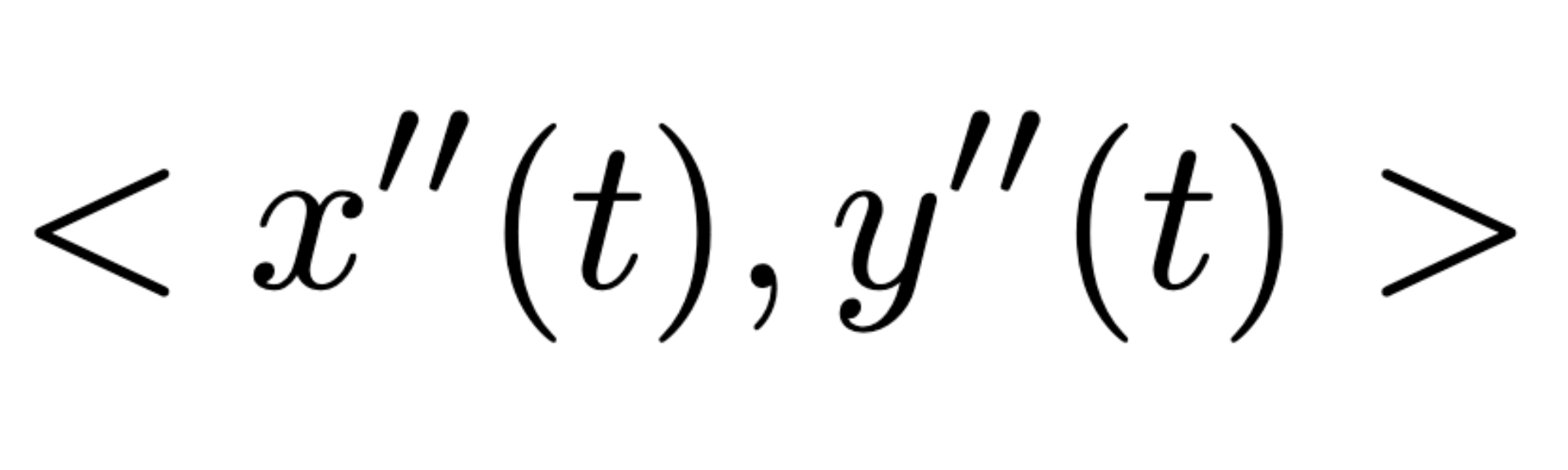
Speed (or magnitude of velocity vector)
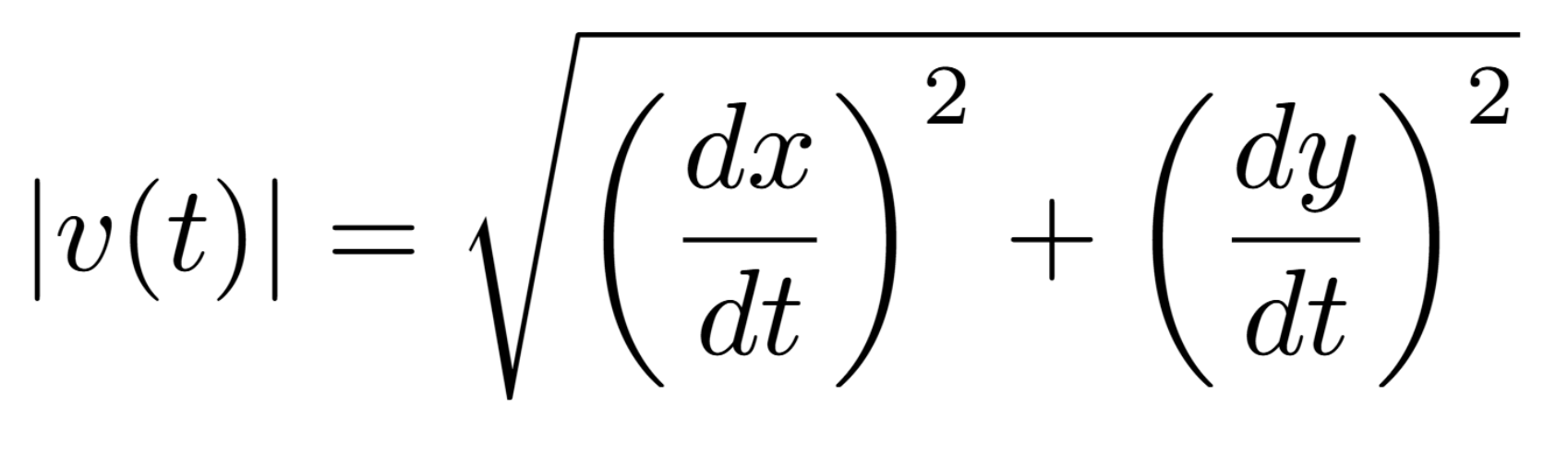
Distance traveled from t = a to t = b (or length of arc)
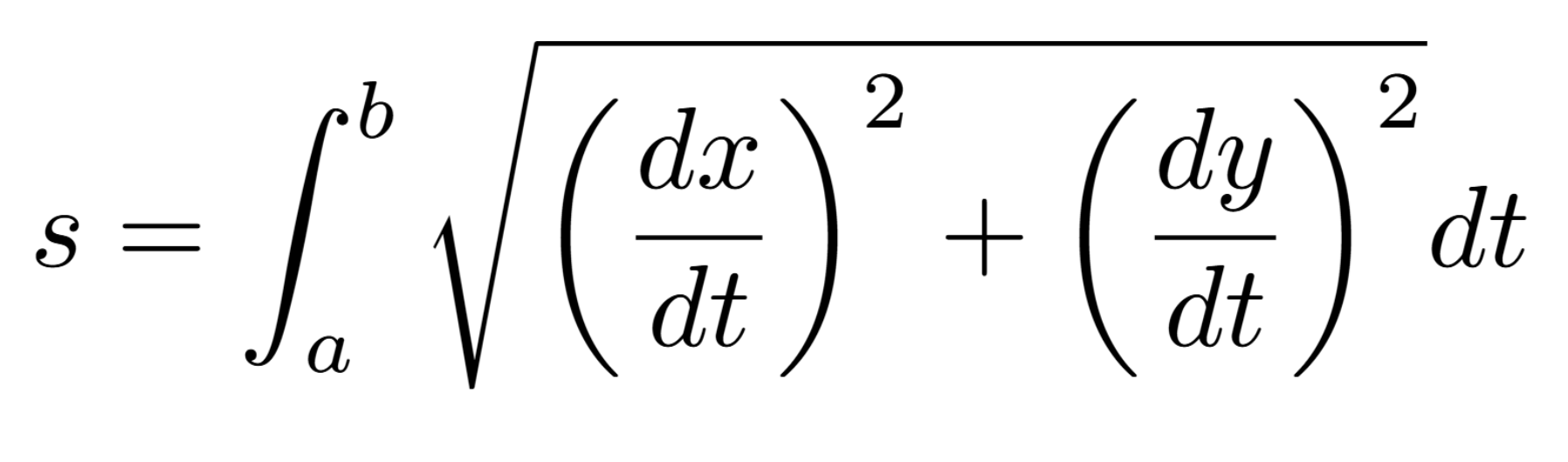
In polar curves, x =
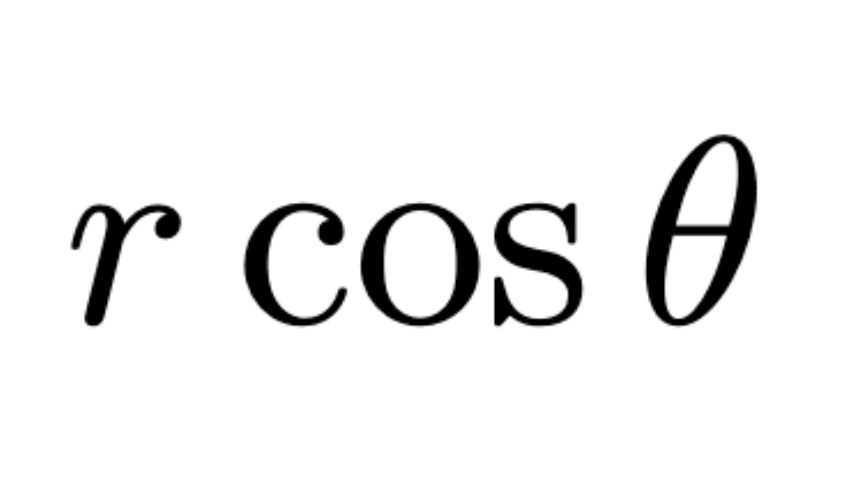
In polar curves, y =
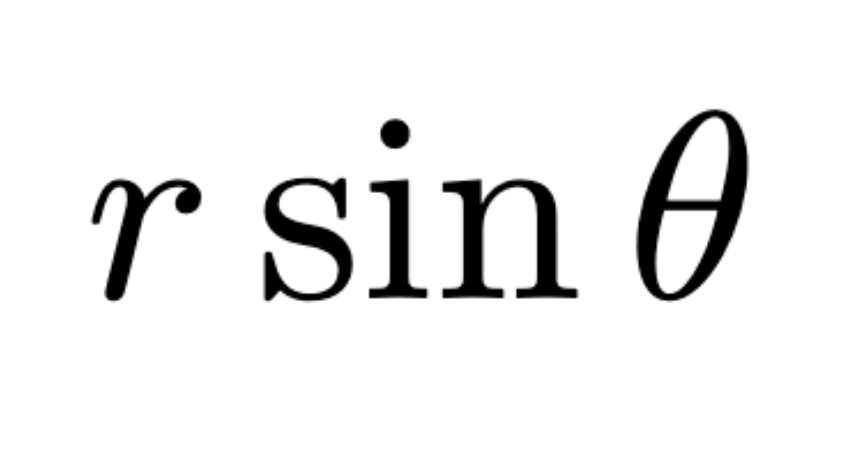
Slope of polar curve
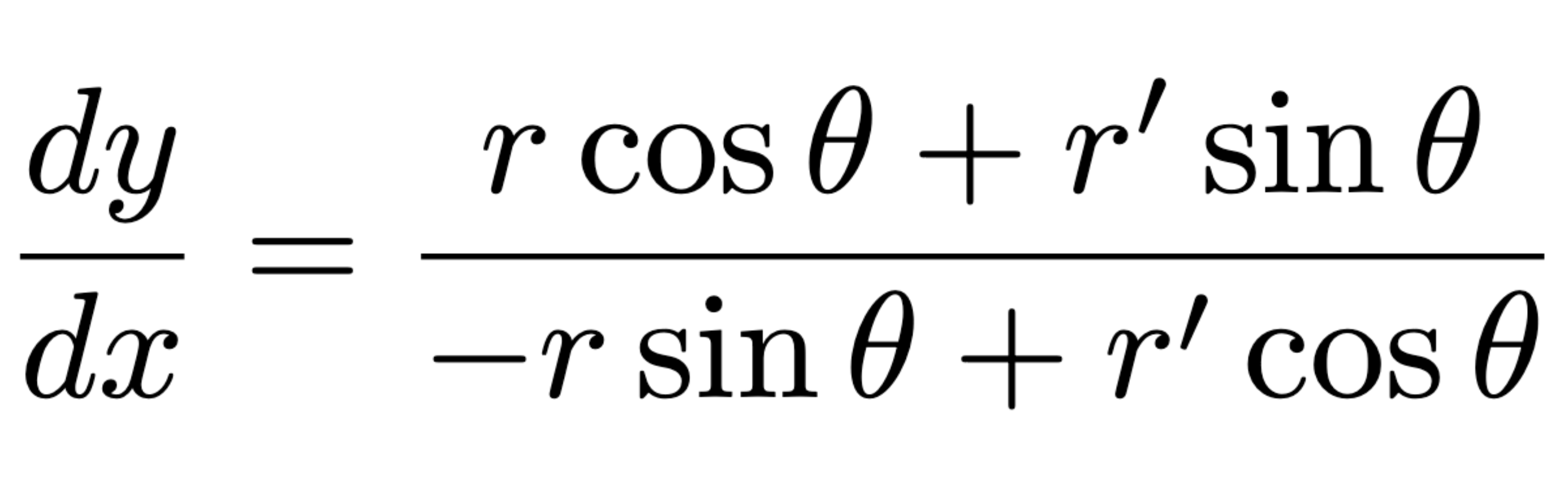
Area inside a polar curve
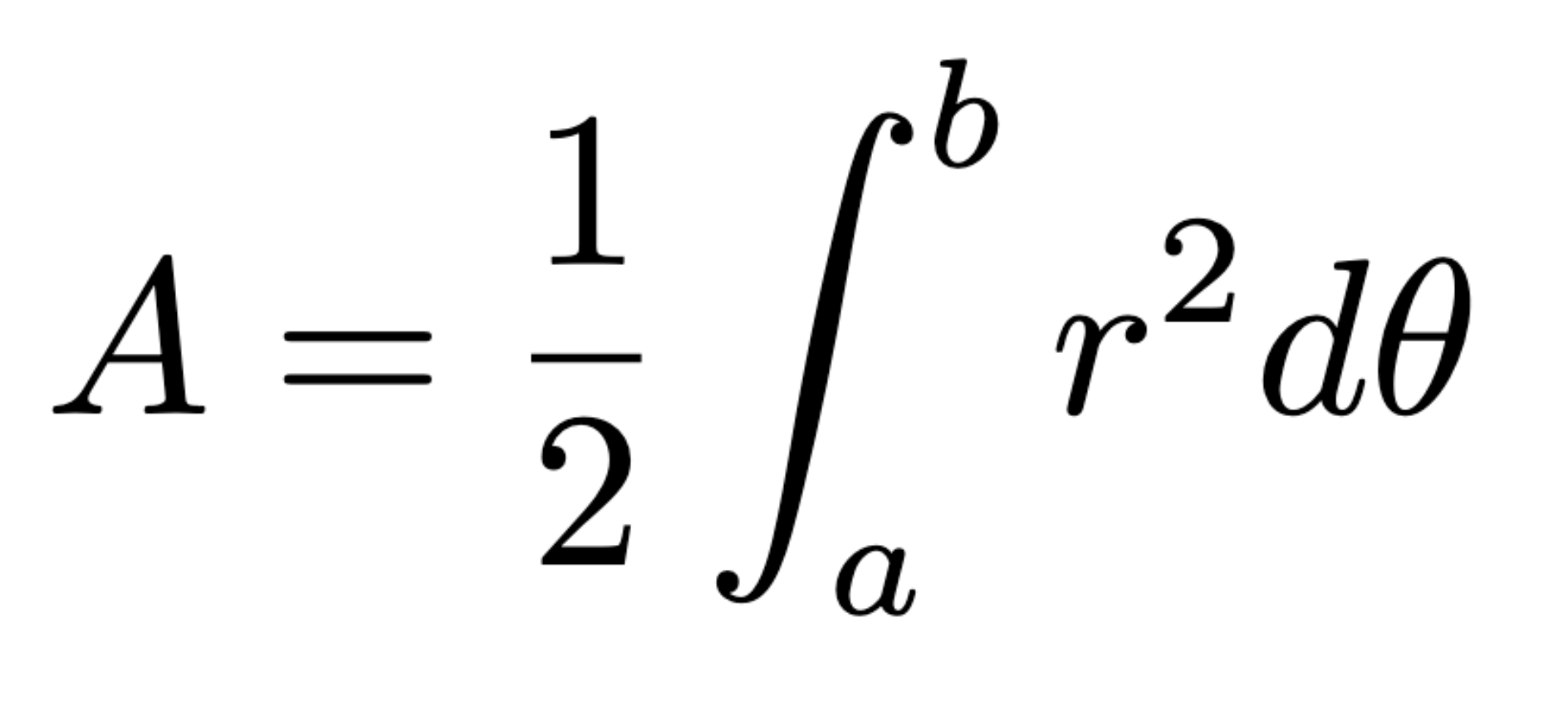
Maclaurin series for ex
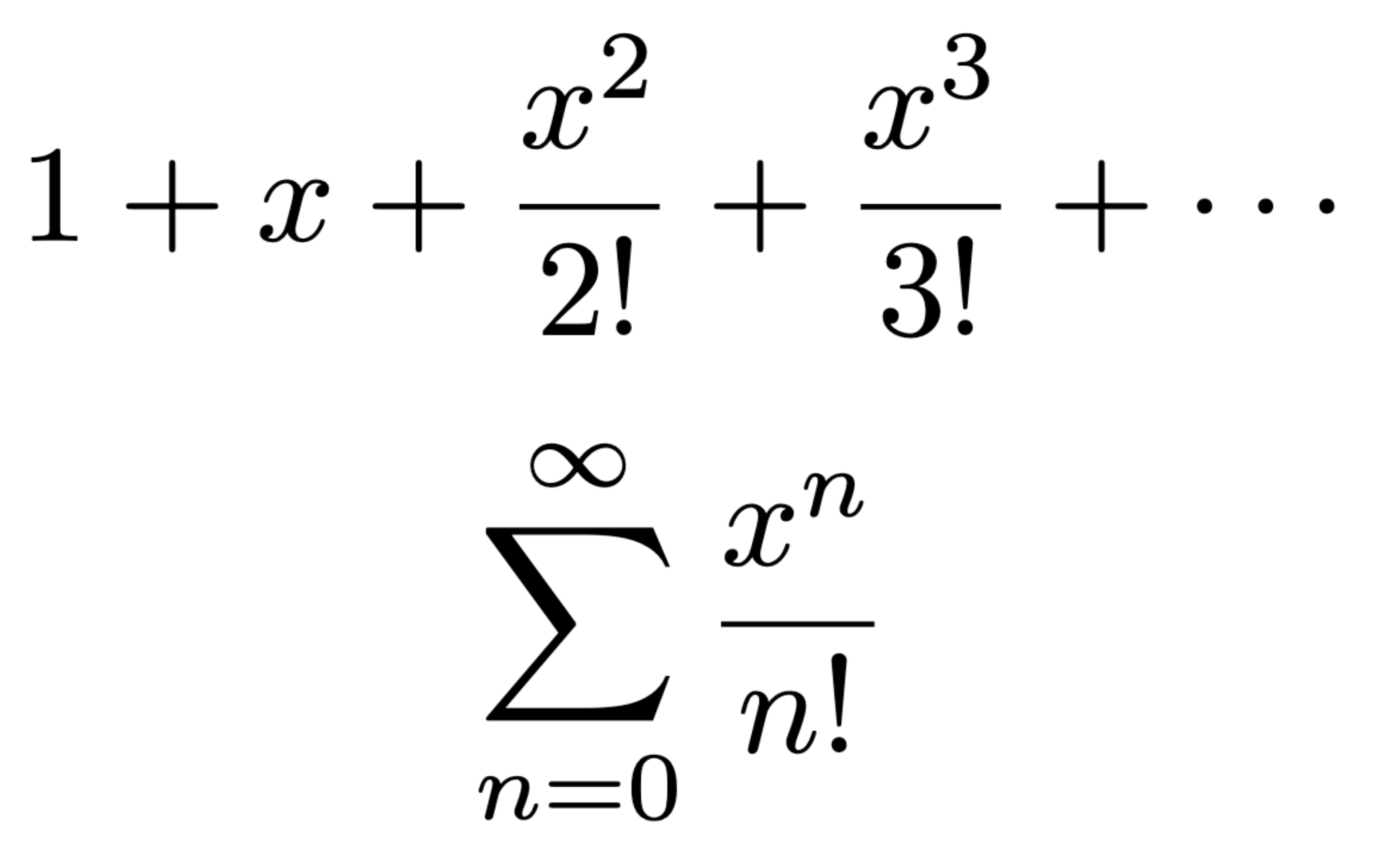
Maclaurin series for cos x
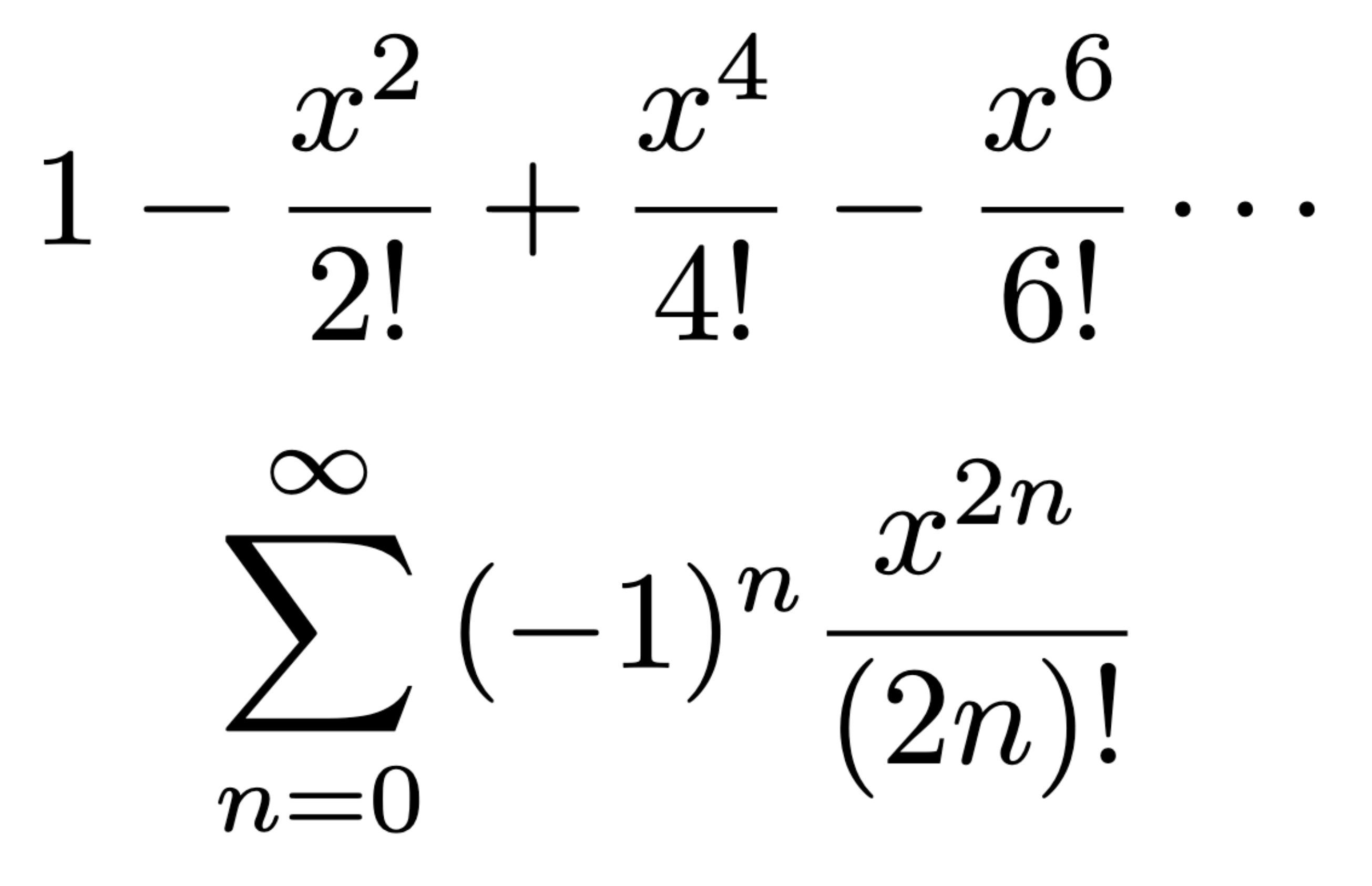
Maclaurin series for sin x
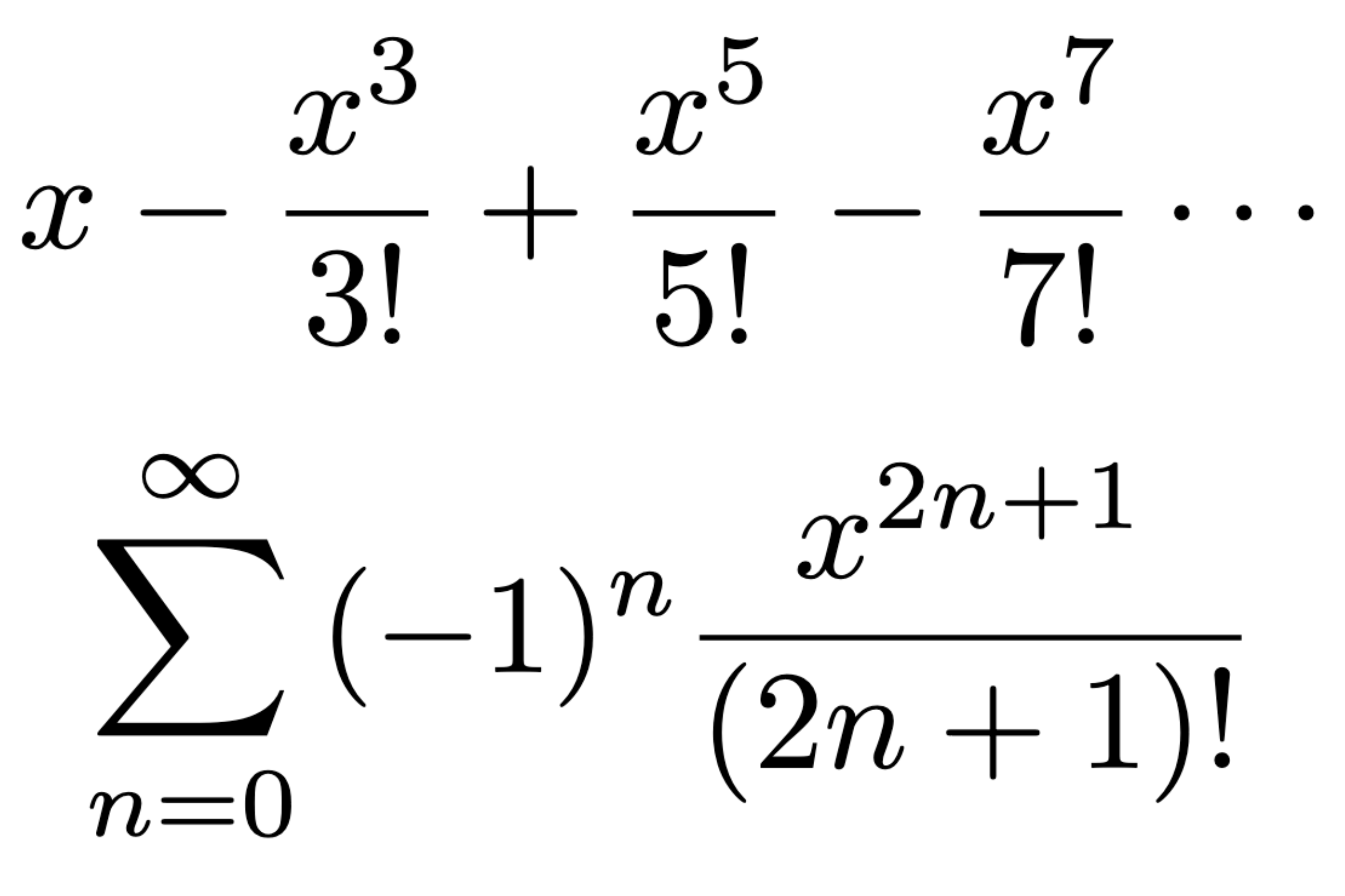
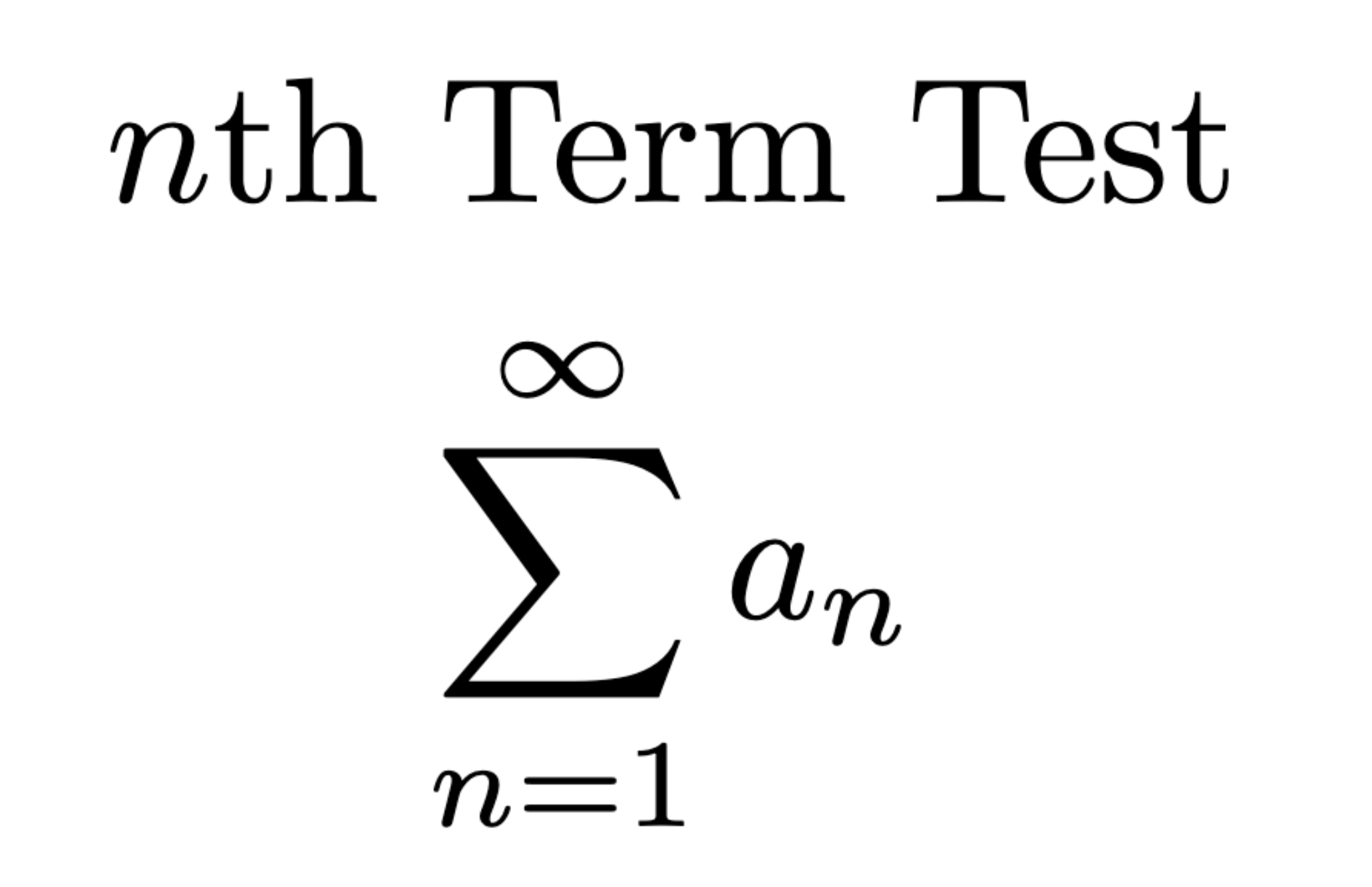
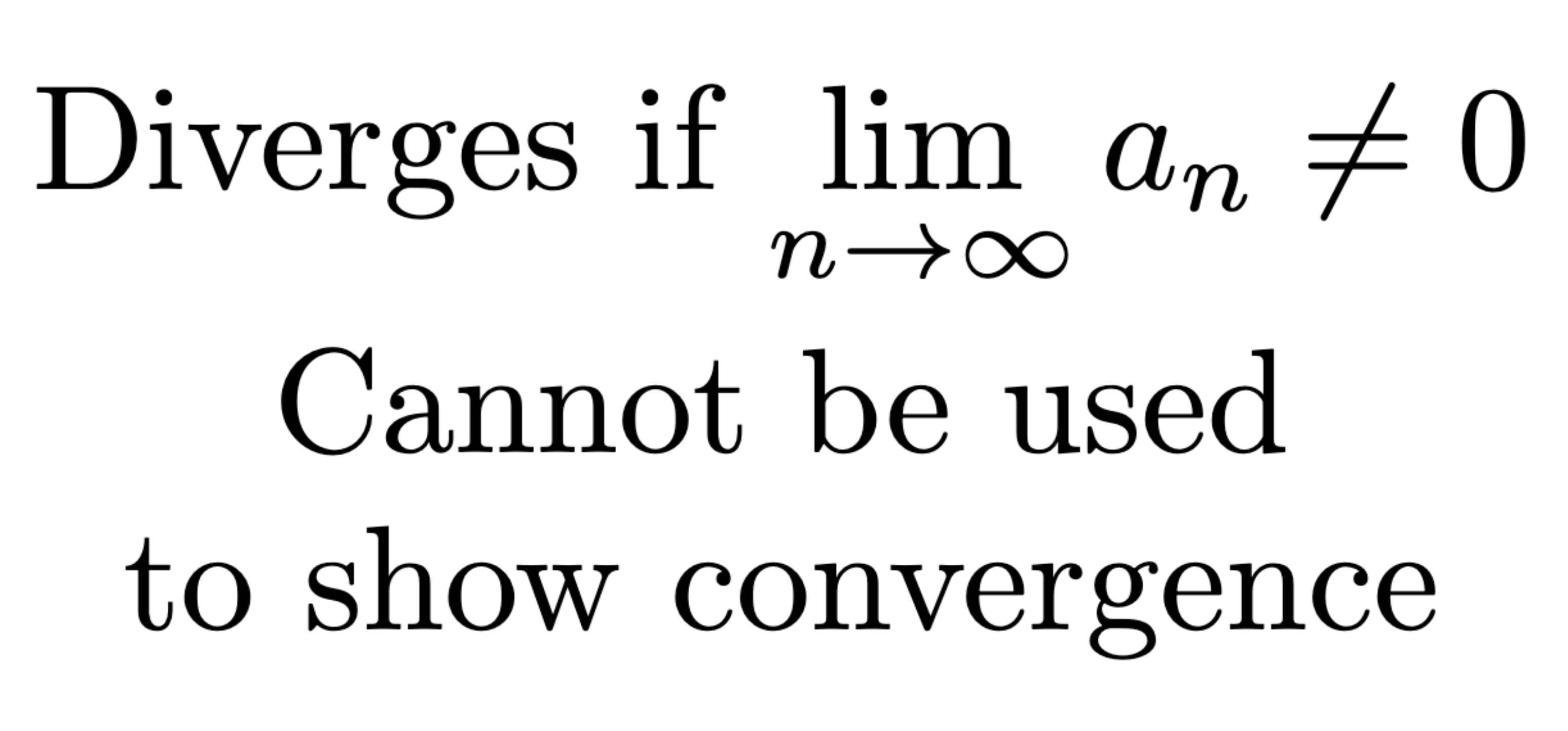
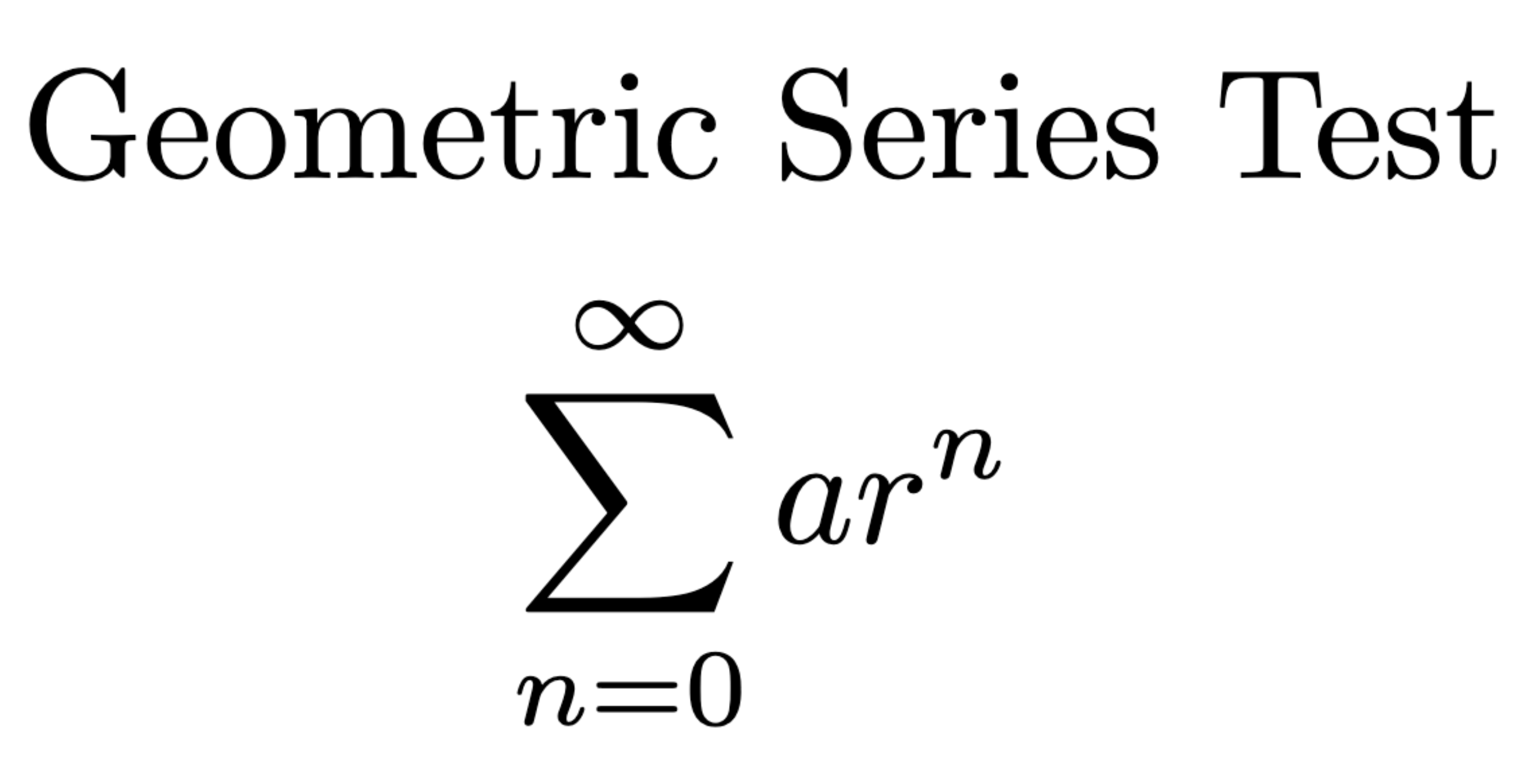
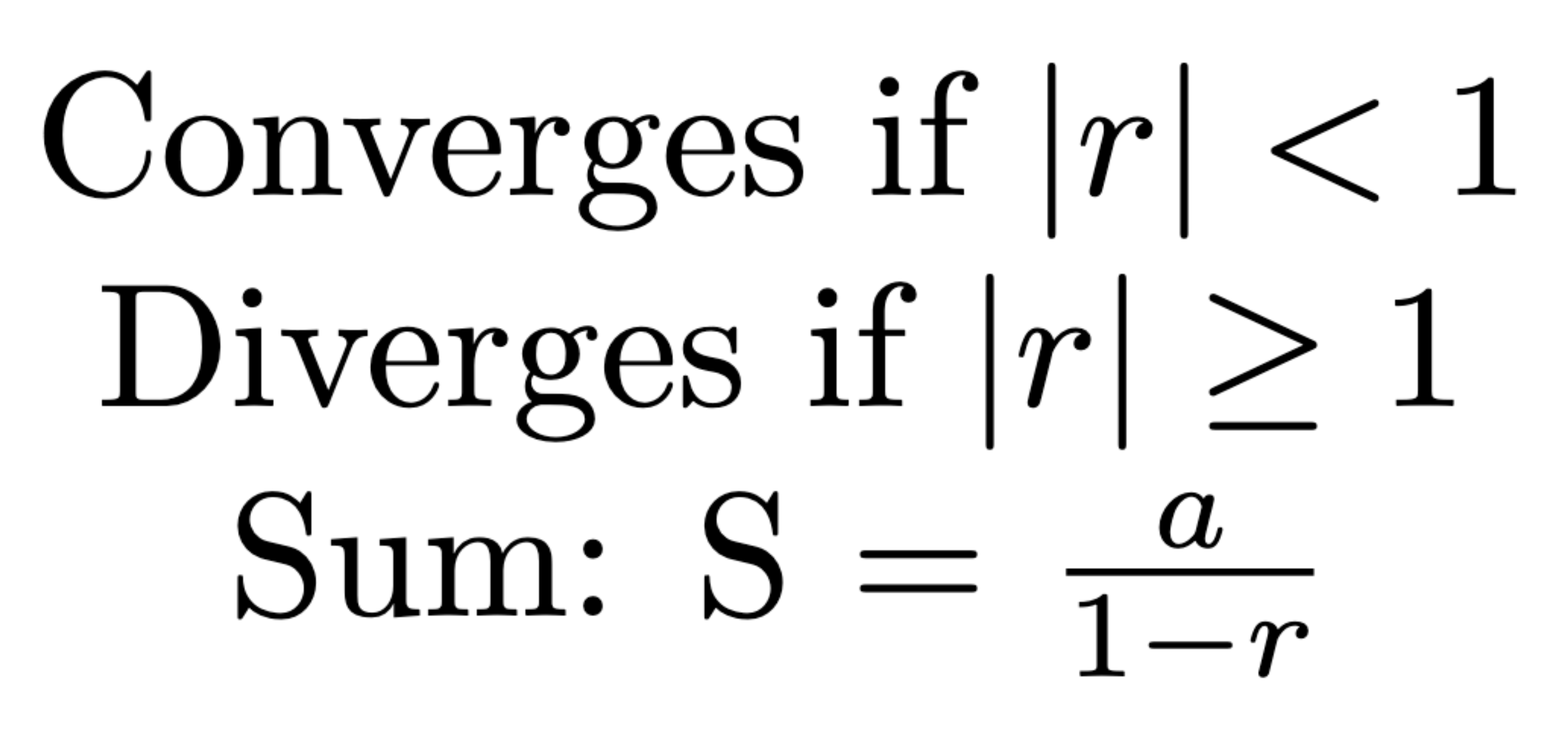
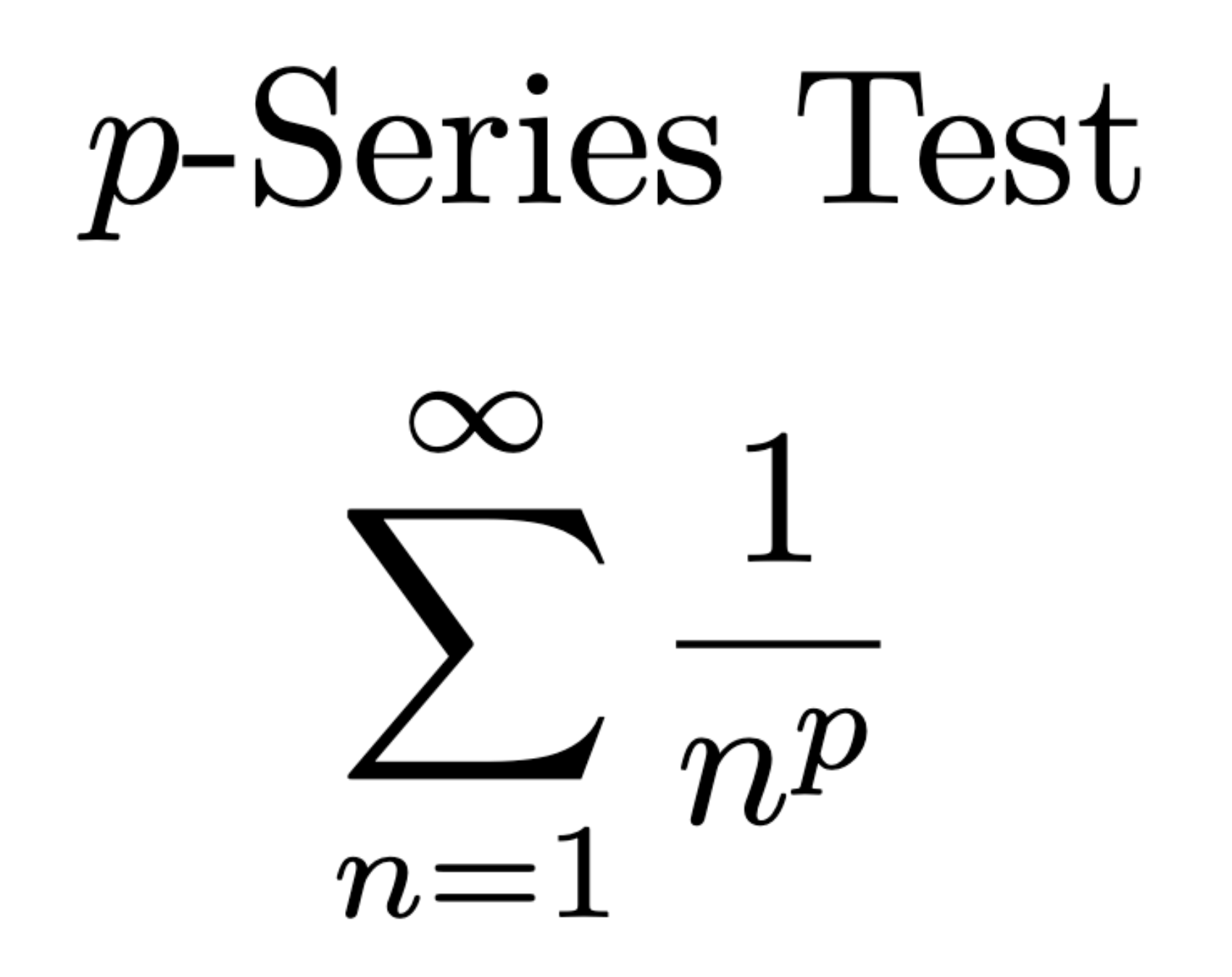
Converges if p > 1
Diverges if p ≤ 1
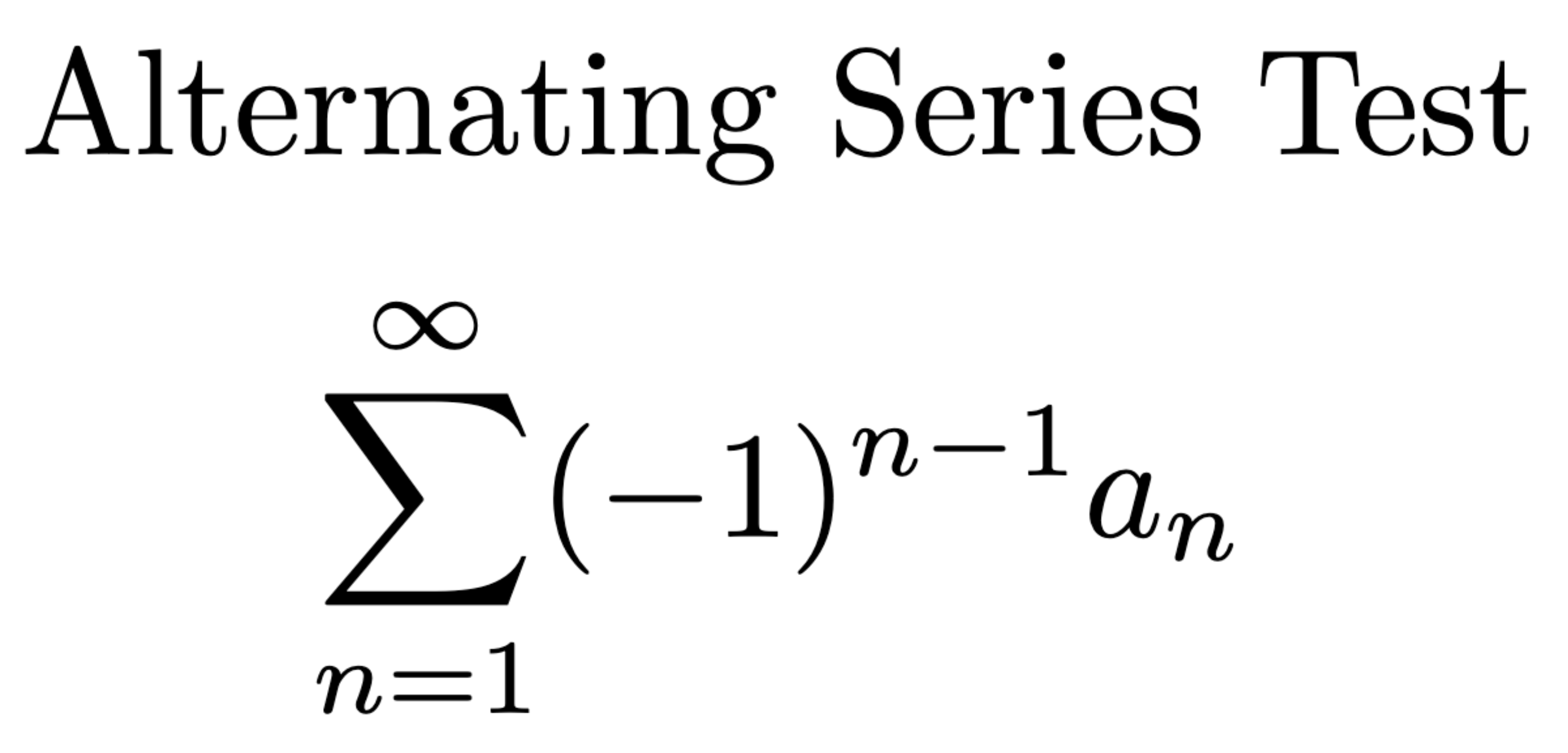

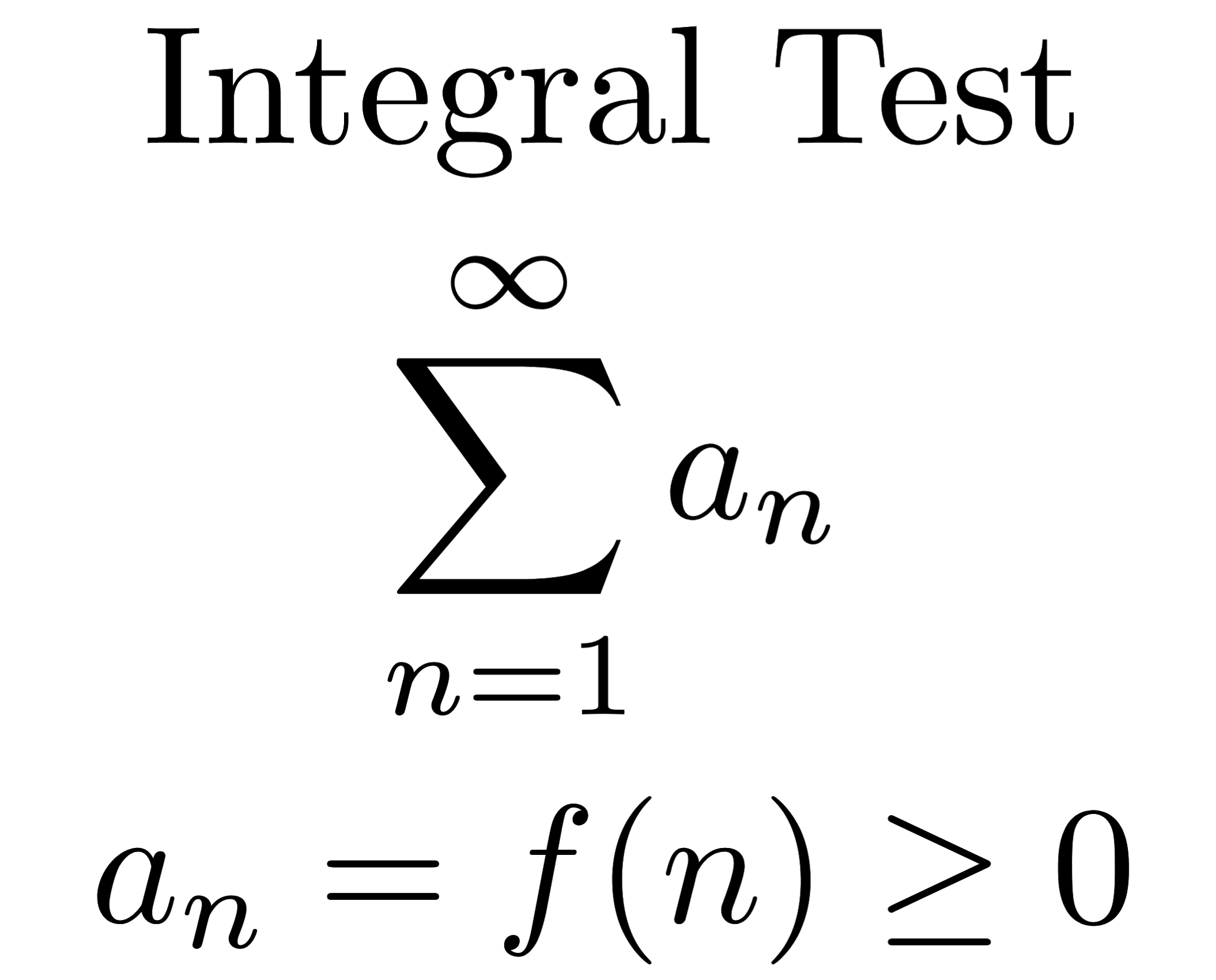
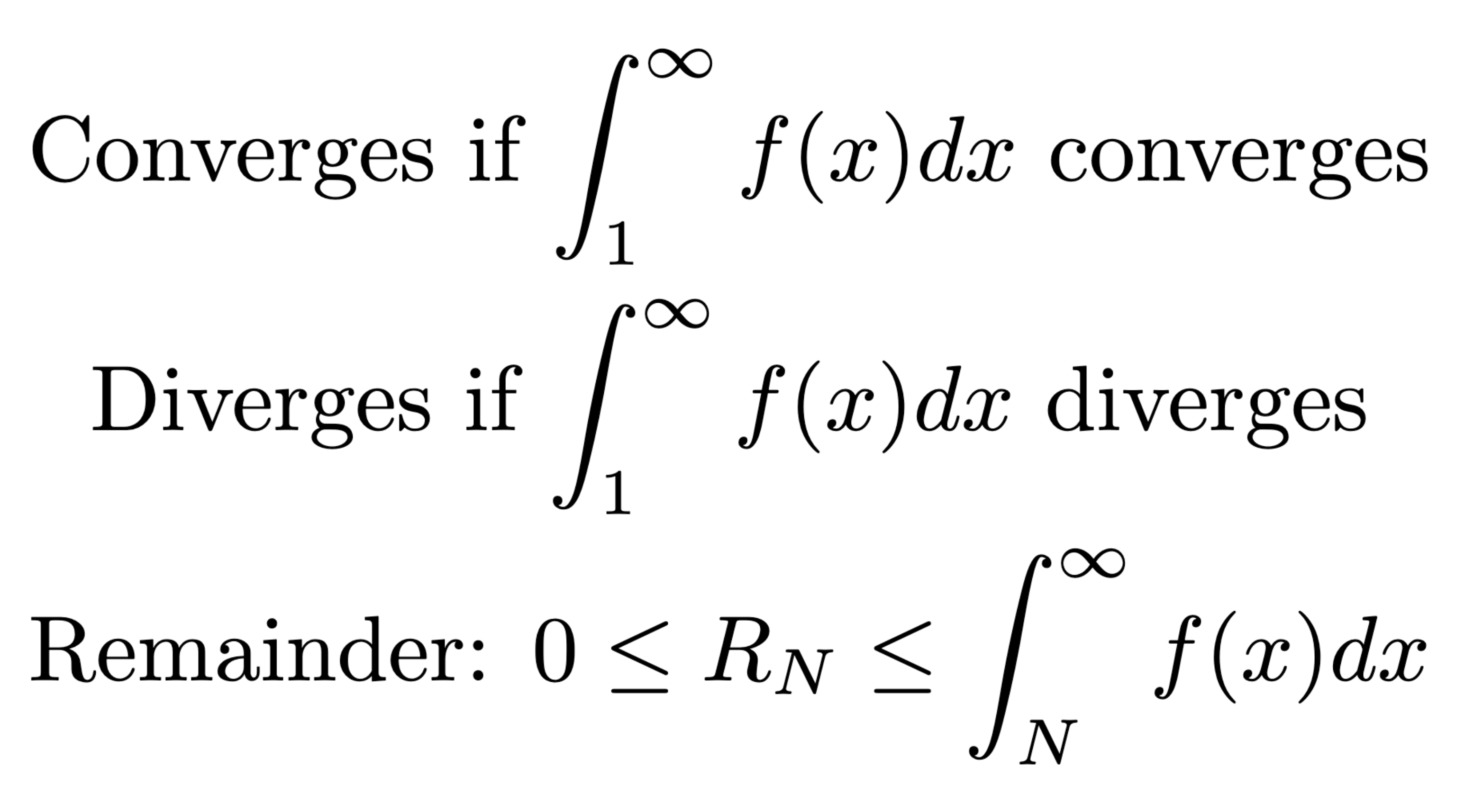
In order to use the Integral Test, the function f(n) must be…
positive, continuous, and decreasing
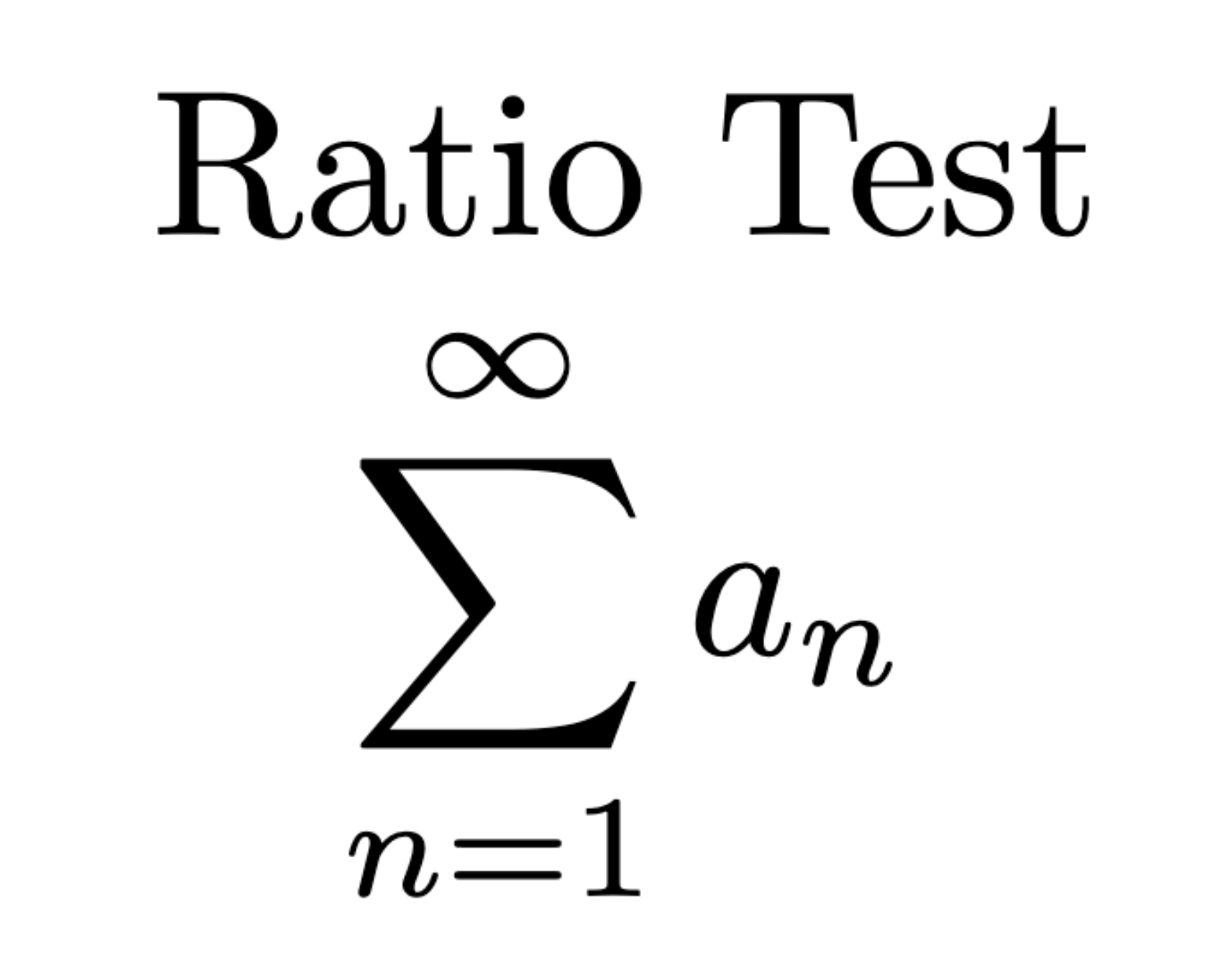
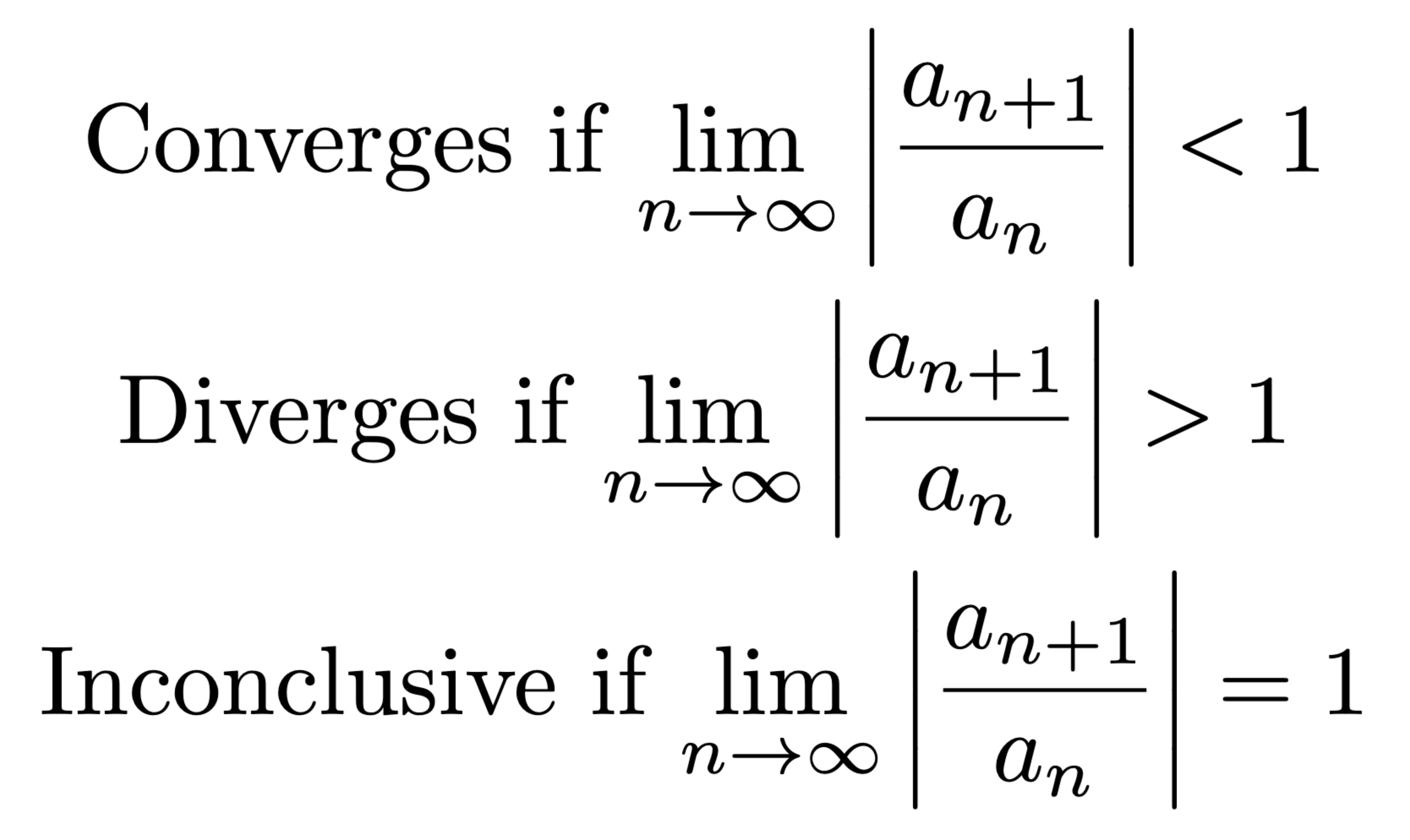
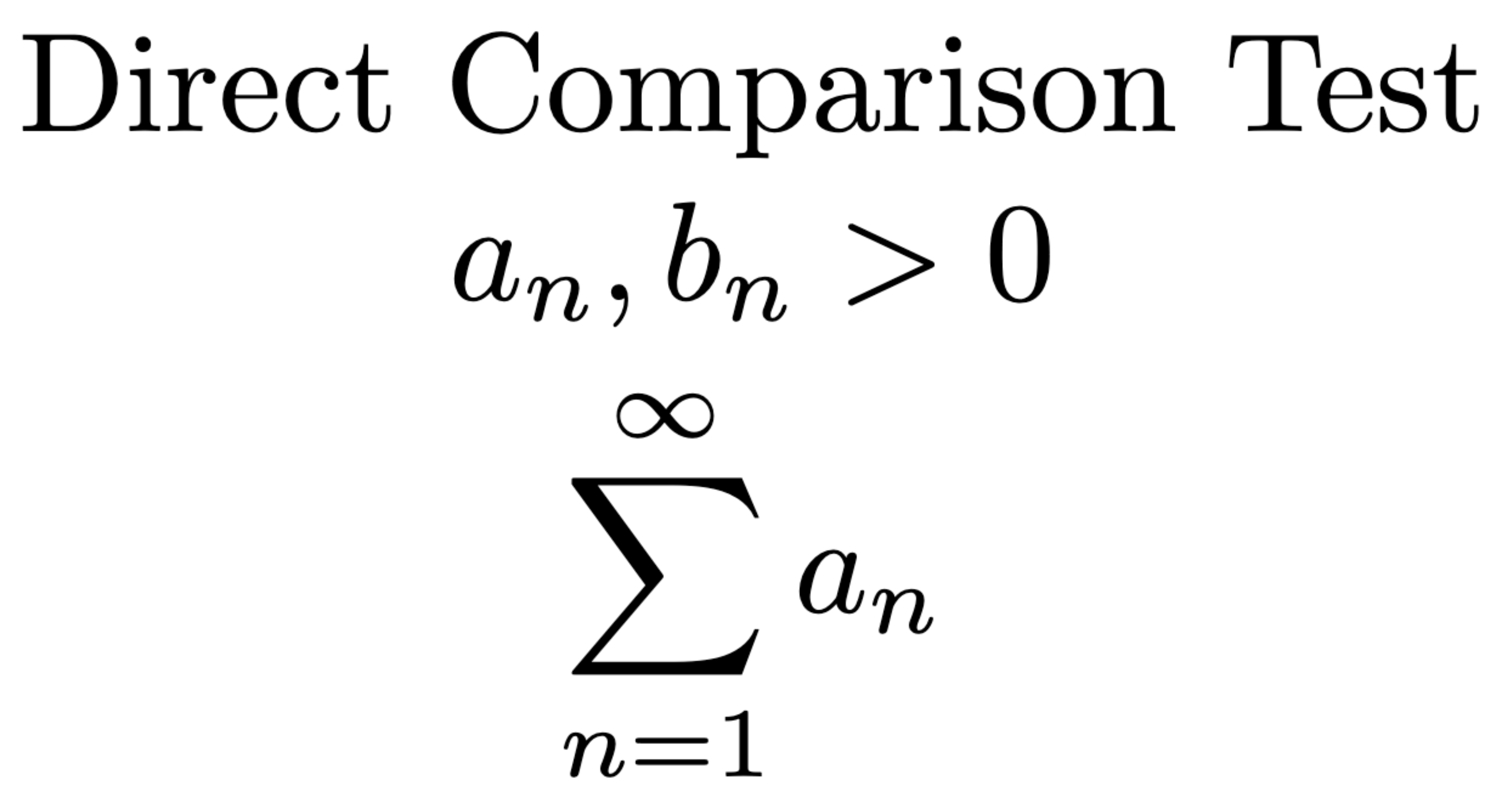
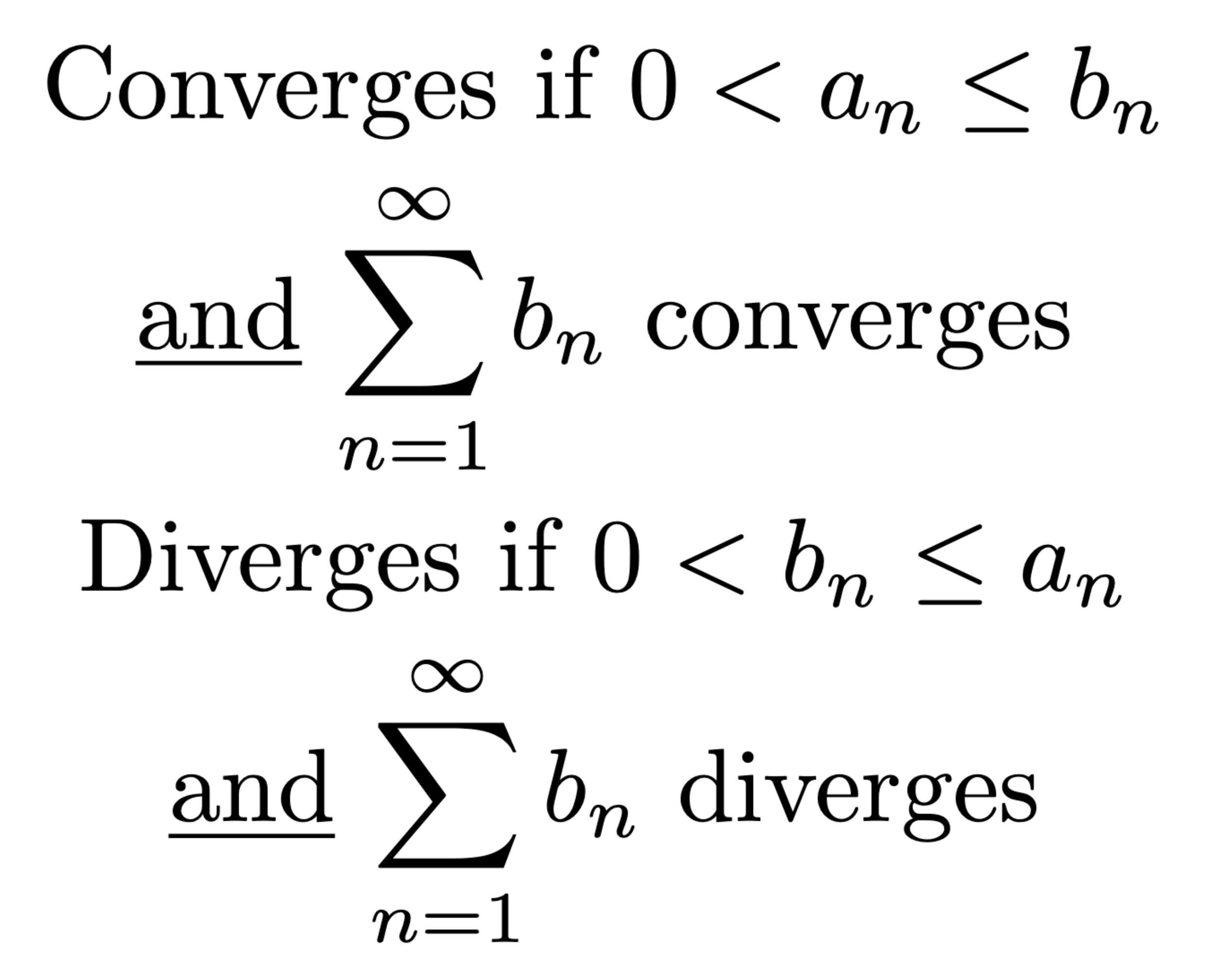
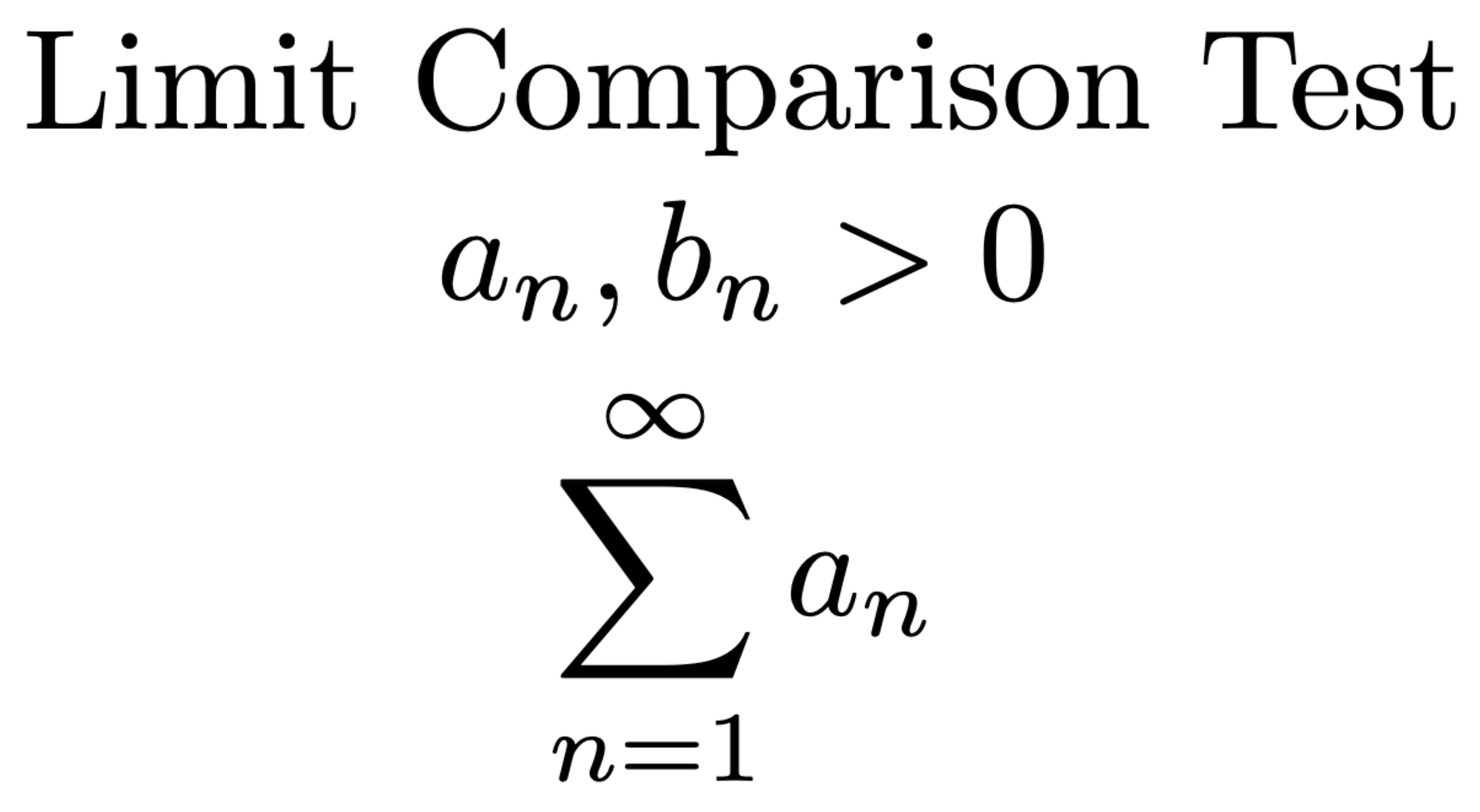
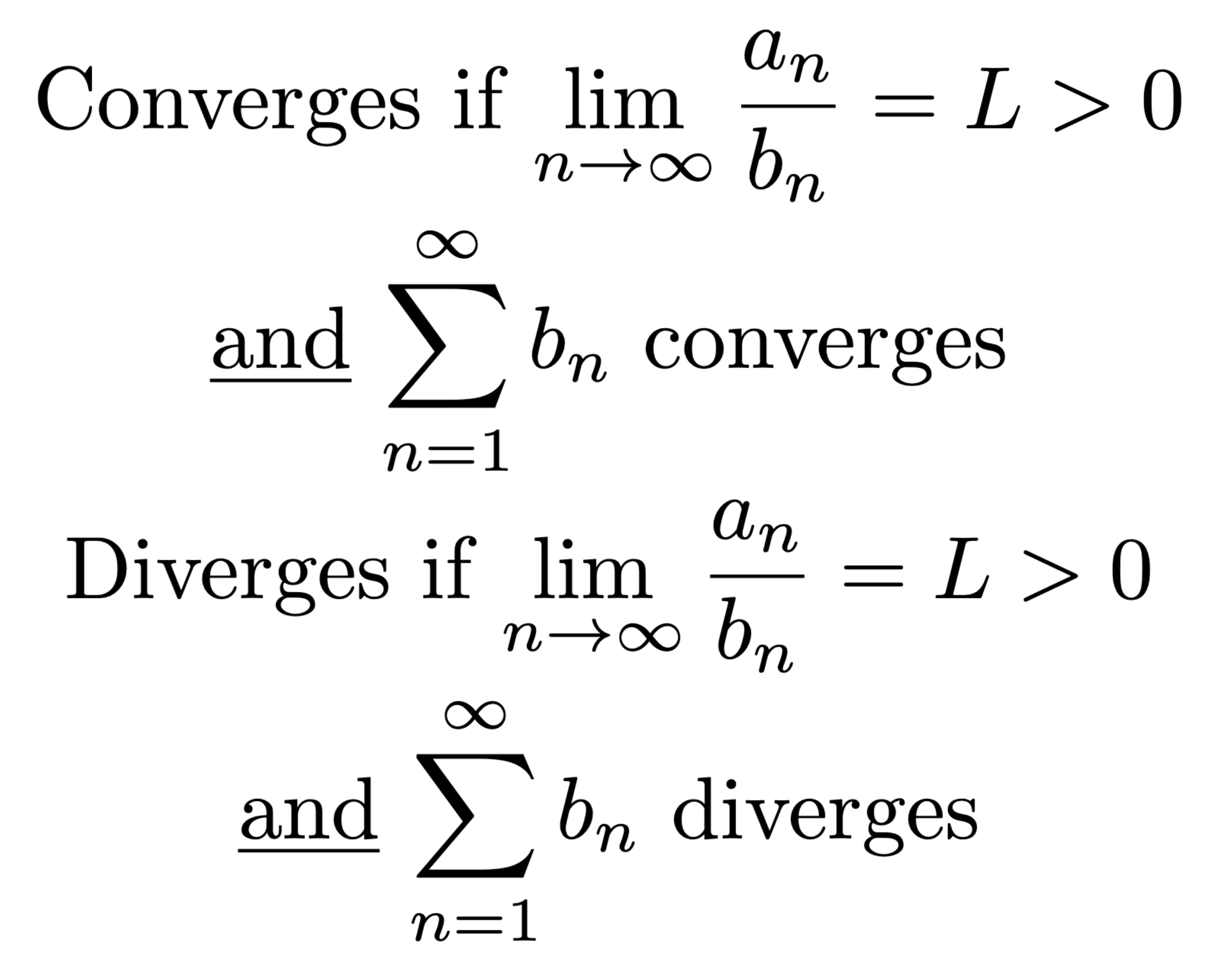
Absolute Convergence
Implies Convergence