Geo U10: 3D Figures

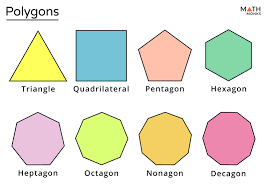
U10: Polygon

Closed 2-D shape whose sides are segments

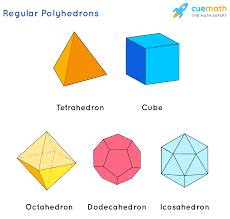
U10 Polyhedron

Closed 3-D shape whose faces are polygons (no curves)

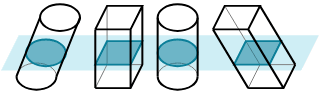
U10 Cavaliers’s principle (3D)

If 3D figures have the same height and equal areas everywhere along the height then they have the same volume

(You must know the height of the object and the width along the height, or the base)

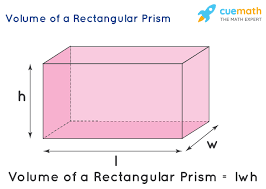
U10 Rectangular prism (volume equation)

lwh=V

LENGTH X WIDTH = Base —> full equation could be: Base area x height = volume

U10 Volume of prism (equation)

Vprisim = Base area x height

= B x h

Note: Base AREA used for polygons AND height is defined as the distance between the bases, height is ALWAYS perpendicular to the bases

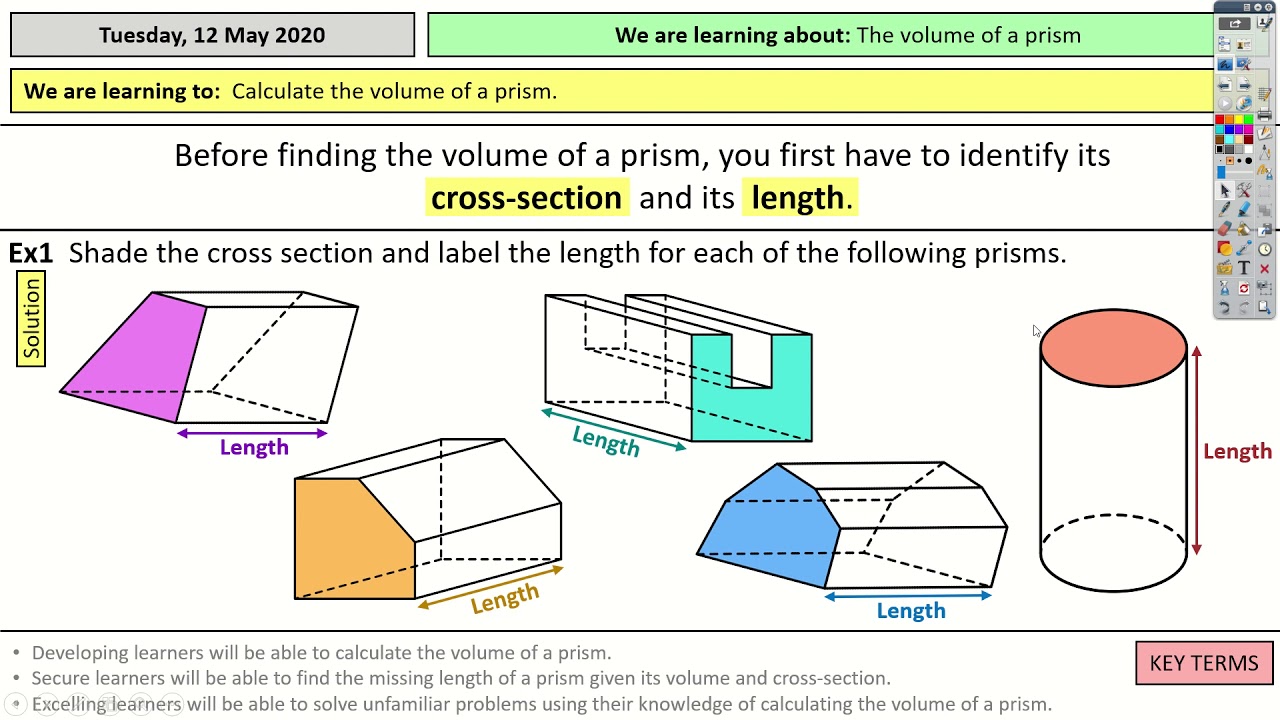
U10 Height of prism

Height of a prism is the distance between the bases, height is always perpendicular to the bases

U10 Other equations (volume)

Volume/base area = height

Volume/height = base area

Base area x height = volume

U10 Prism (definition and equation) also: define “height” of a prism

Definition: A 3-D figure with 2 bases that are congruent and parallel and whose other faces are parallelograms

Equation: Base area x height = Volume AKA: B x h = V

Height: of a prison is the distance between the bases, height it always perpendicular to the bases

U10 Conversion between cubic feet and gallons (and how to convert)

1ft³ = 7.48 gallons

Feet³ = 7.48gal/1 foot —> feet cross cancel and the fraction you multiply it back is equal to one

U10 Intersection

Where shapes cross AKA: when a set of points is in all shapes

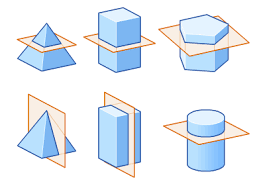
U10 Cross section

Intersection of a plane and 3D object/figure

U10 Truncate

Means to cut off

U10 Density (and three equations)

Denser objects have more mass for the same volume

D = m/v

m = d x v

V = m/d

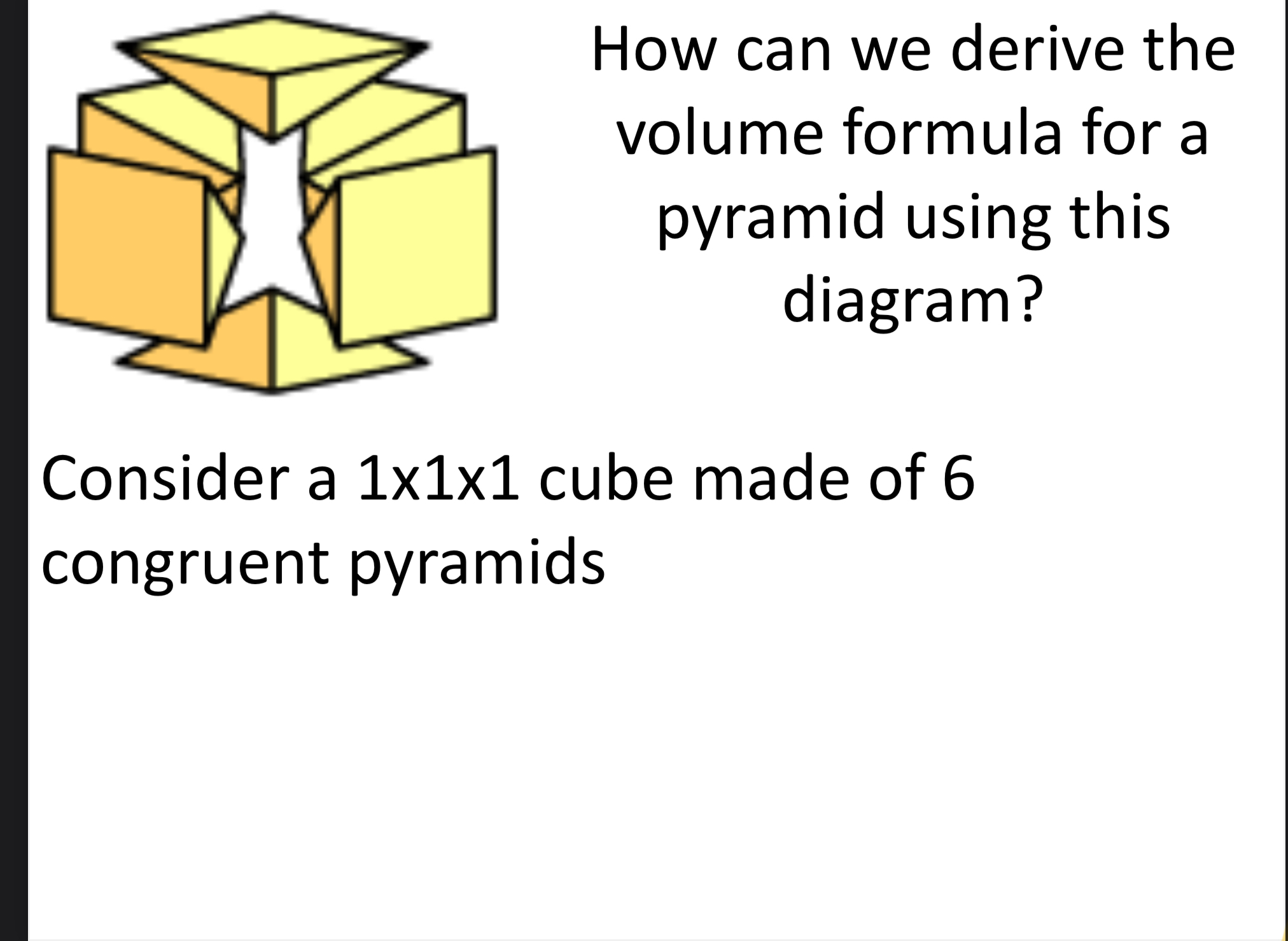
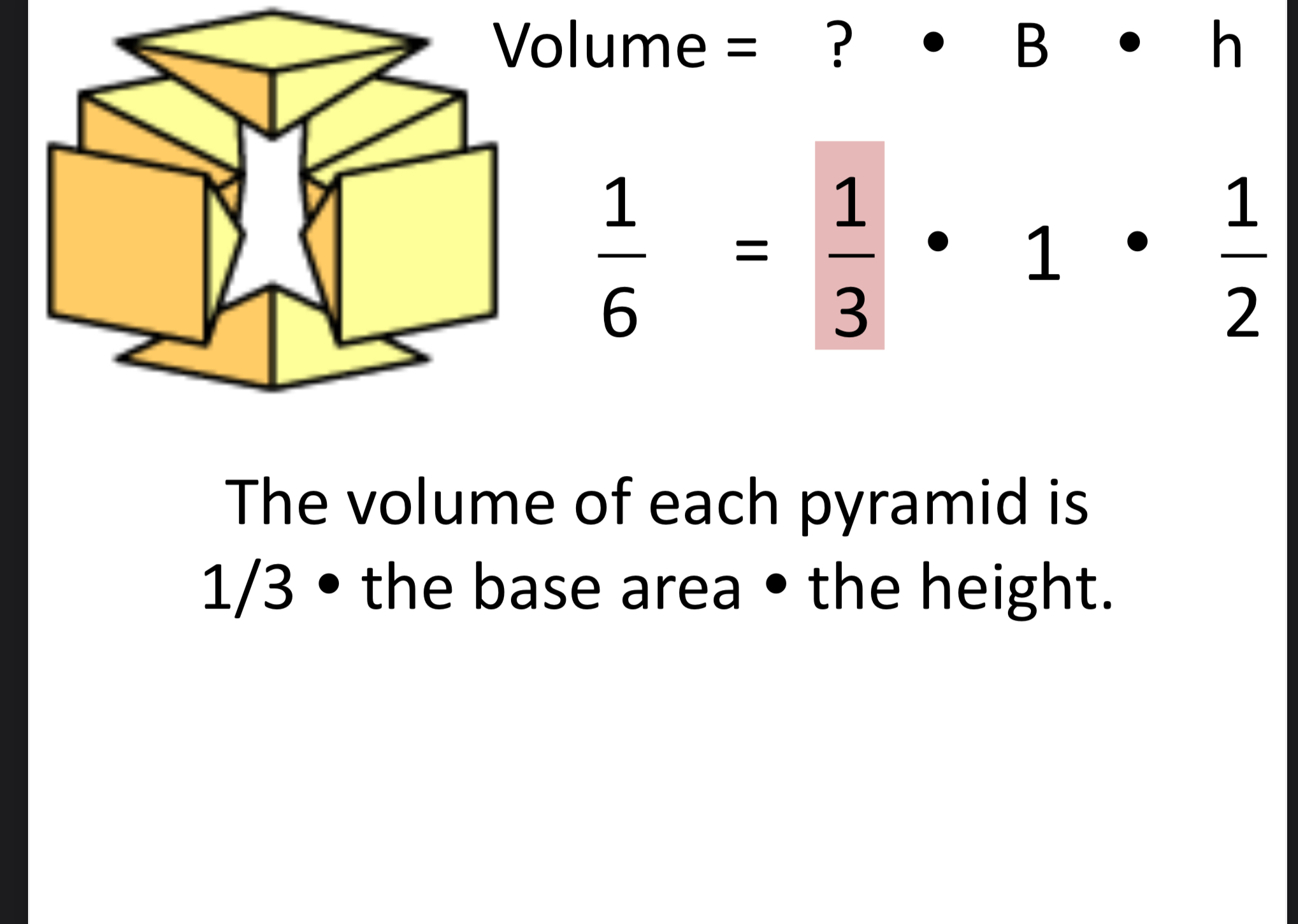
U10 Pyramid and equation for volume

Pyramid: 3D figures with triangular lateral faces and polygon bases

Equation: Vpyramid = 1/3 (Base area x height) = Bh/3

Note: 1/3 because it’s one third of a cube

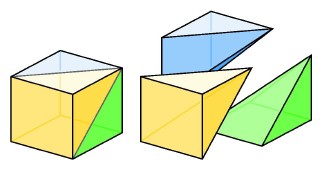
U10 Max sides of a cross section

The number of faces

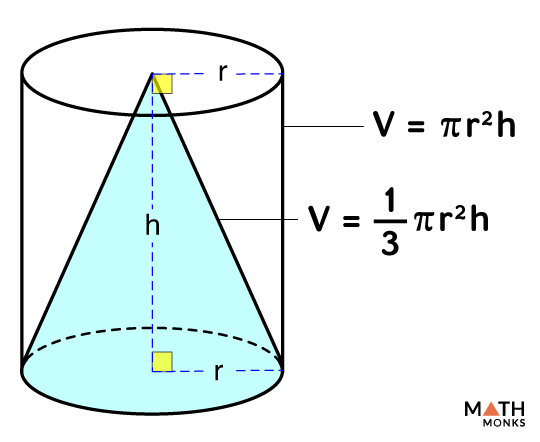
U10 Volume of a cone (equation)

Vcone = (πr² x h)/3

—> contains less volume than may appear, it is one third of a cylinder

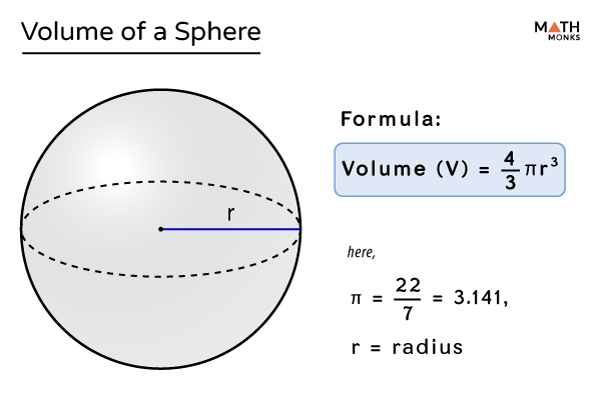
U10 Sphere (definition and equation)

Sphere: set of points equidistant from a center point

ratio of Vsphere:Vcylinder = 2:3

Vsphere = 4/3 πr³

U10 Cylinder (volume equation and comparison to sphere)

V = πr²h

Compared: sphere is 2/3 of the volume of a cylinder

How to remember: base is circle times height

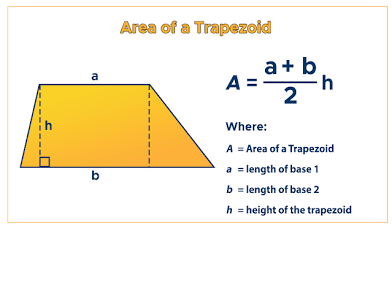
U10 Trapezoid AREA formula

A = ((b1 + b2)/2)) (h)

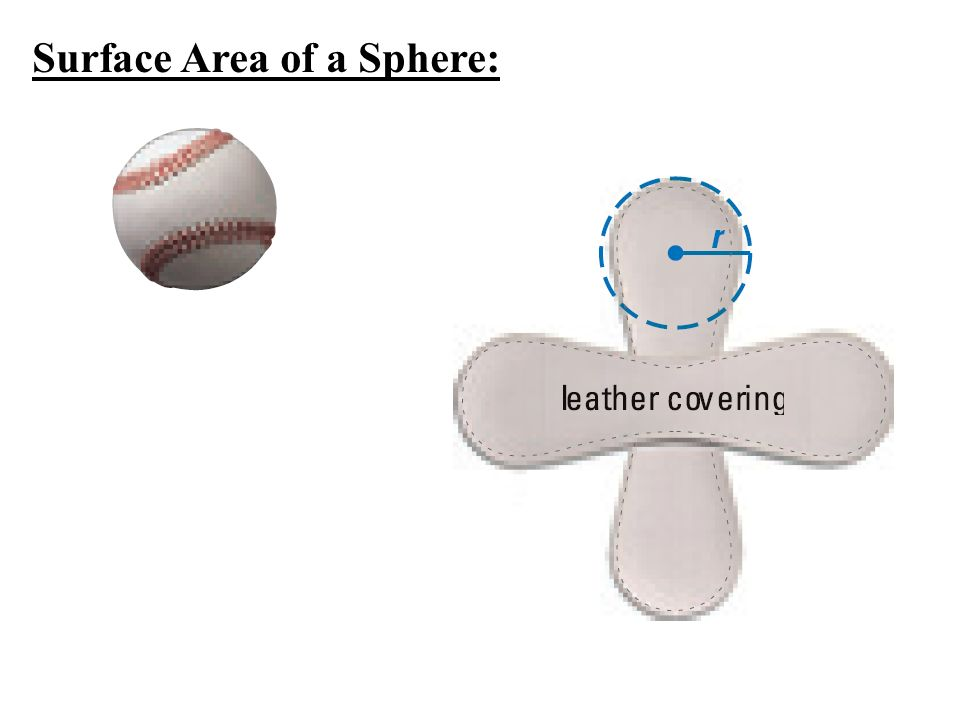
U10 Surface Area of a sphere and why?

Surface area of a sphere = 4πr²

Think about it like a baseball: 4 circles if you lay out the pieces

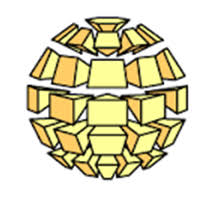
U10 How to use pyramids to determine the volume of a sphere?

The pyramids’ height is the radius of the sphere.

The sum of the volumes of the pyramids is…

1/3(B1r) + 1/3(B2r) + 1/3(B3r) +….

Factoring we get: 1/3r(B1 + B2 + B3+…)

The sum of all the bases areas is the surface area of the sphere, which has the formula 4πr²

We can substitute this into the “factoring we get:” equation to get a NEW equation: 1/3r(4πr²) = 4/3πr³

This is the volume formula for a hemisphere!!

Vsphere = 4/3πr³

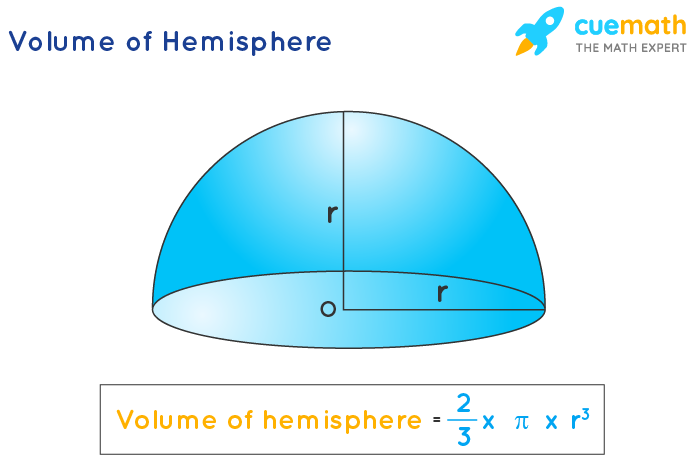
U10 What is a hemisphere (description and volume formula)

3D shape that is half of a sphere.

Vhemisphere = (2/3)πr³

U10 If the edges of a rectangular prism (or any 3D shape) double, how does the surface area change? How does the volume change?

Edges: times n

Area: times n²

Volume: times n³

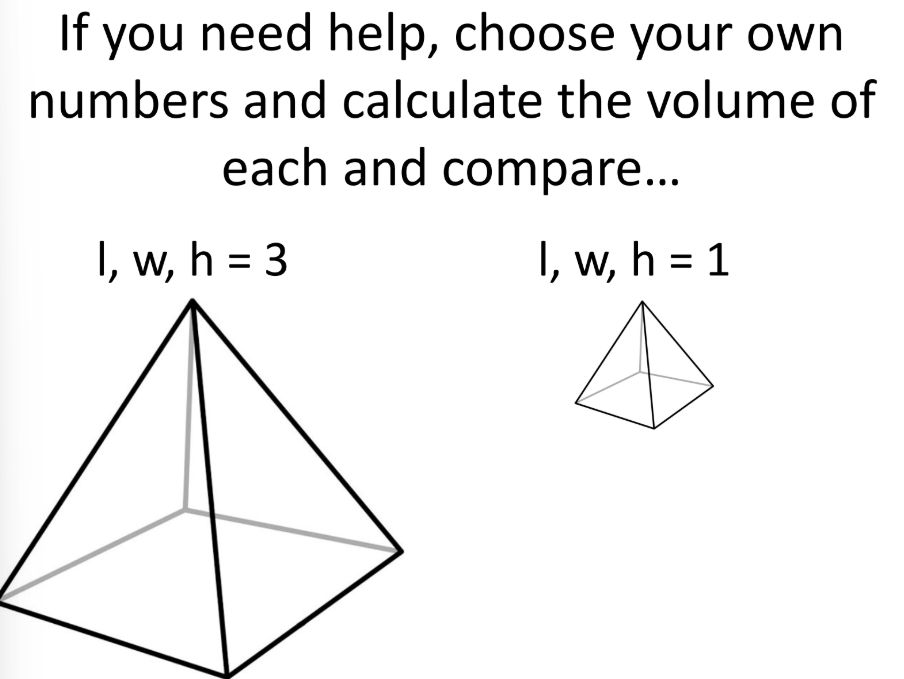
U10 The top 1/3 of a pyramid has what percent of the total volume? If we dilate a pyramid by a scale factor of 1/3, how does the volume change? (KNOW HOW TO PROVE)

The top 1/3 of a pyramid…

(You can use example numbers)

1/27=4% (around)

—> Why? Plug in a pyramid of 1,1,1 versus 3,3,3

If we dilate a pyramid by 1/3…

Edges: n

Area: n²

Volume: n³

U10

U10 Population density

People per area

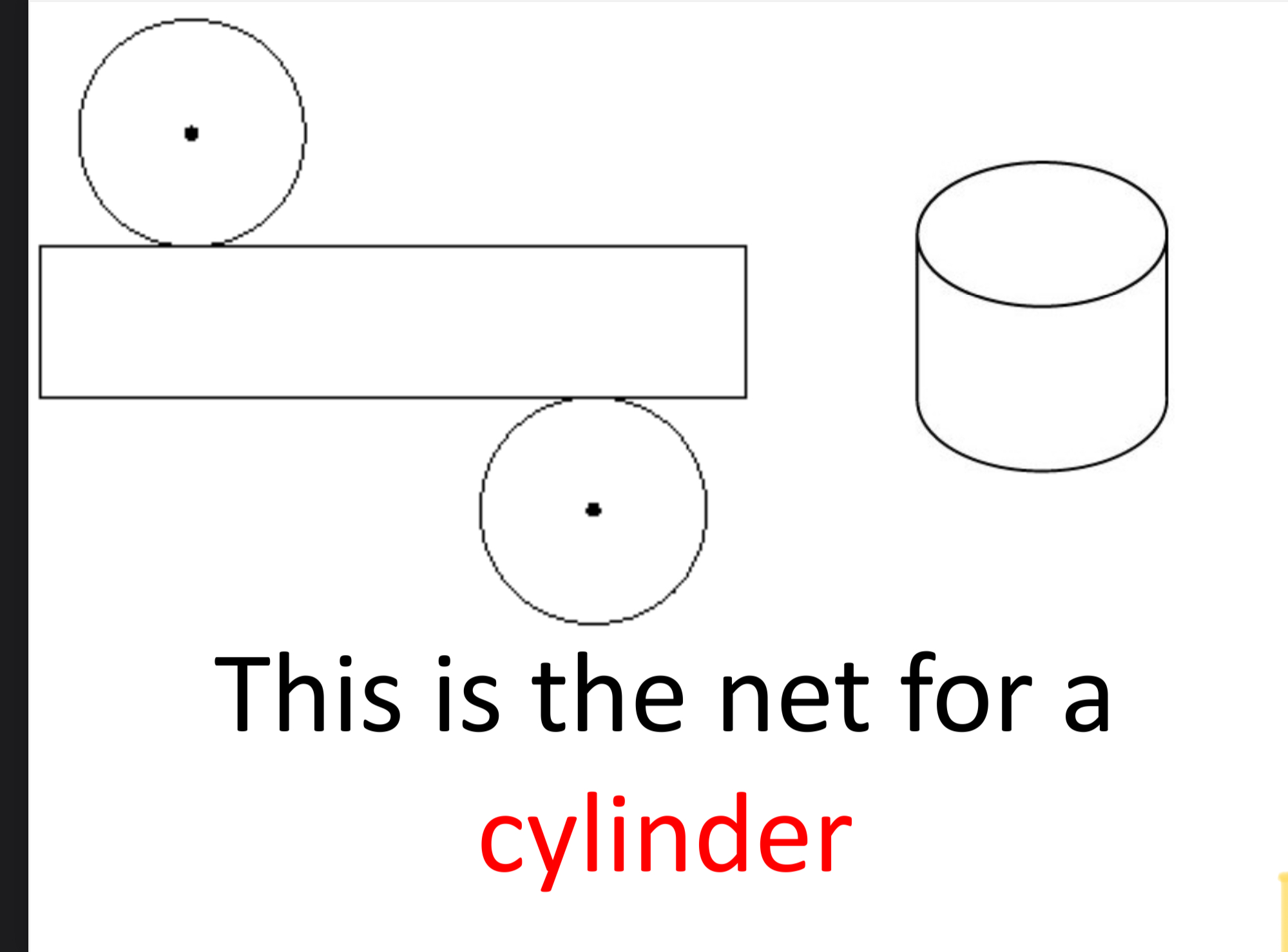
U10 What is a “net”

If you unfold a shape (surface area)

U10 How to do conversions

Do it in one shot!! → multiply everything by a fraction equivalent to one so units cross out. Leaving you with the unit you wanted. MUST be done by multiplying by a fraction equal to one.

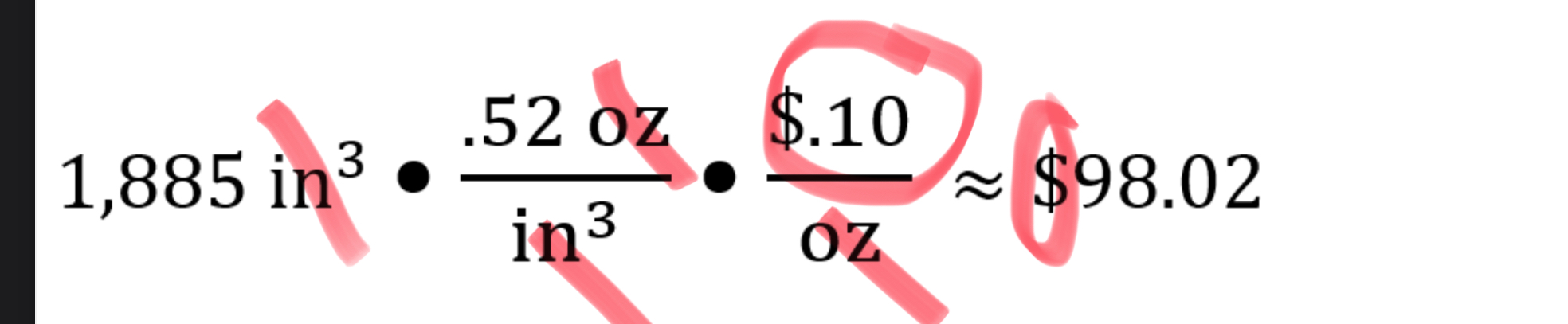
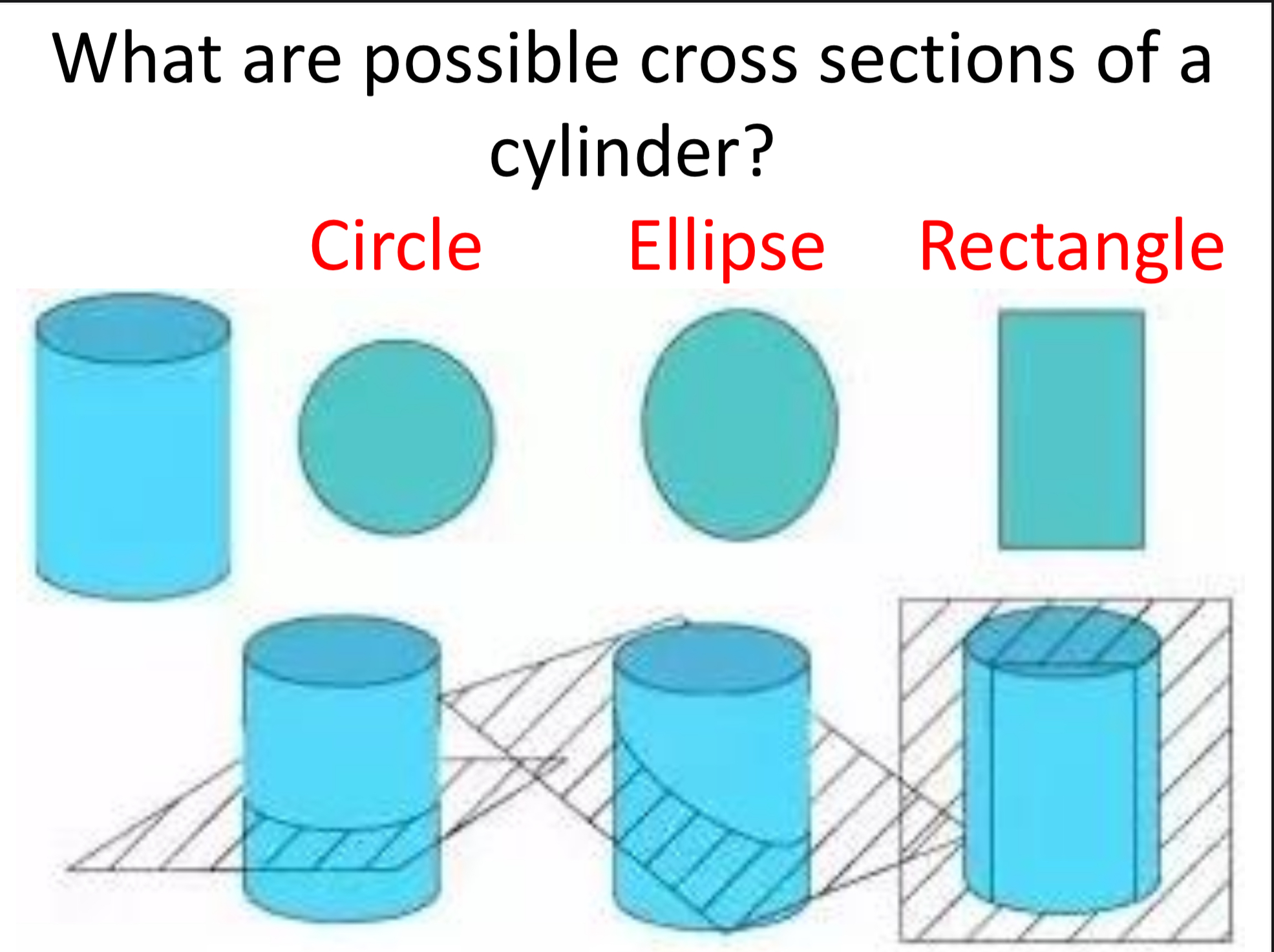
U10 What are the possible cross sections to a cylinder?

Circle, elipse, rectangle

U10 How to find radius from volume of a sphere

Plug it into the volume of a sphere equation. Use "math” button for root of cubed