AP BC Calculus Formula Review

This has all the formulas that we went over in class :) If I'm missing any just let me know!

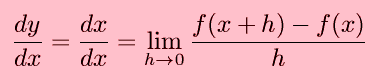
Derivative Standard Form

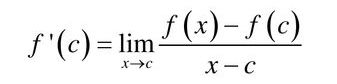
Derivative Alternate Form

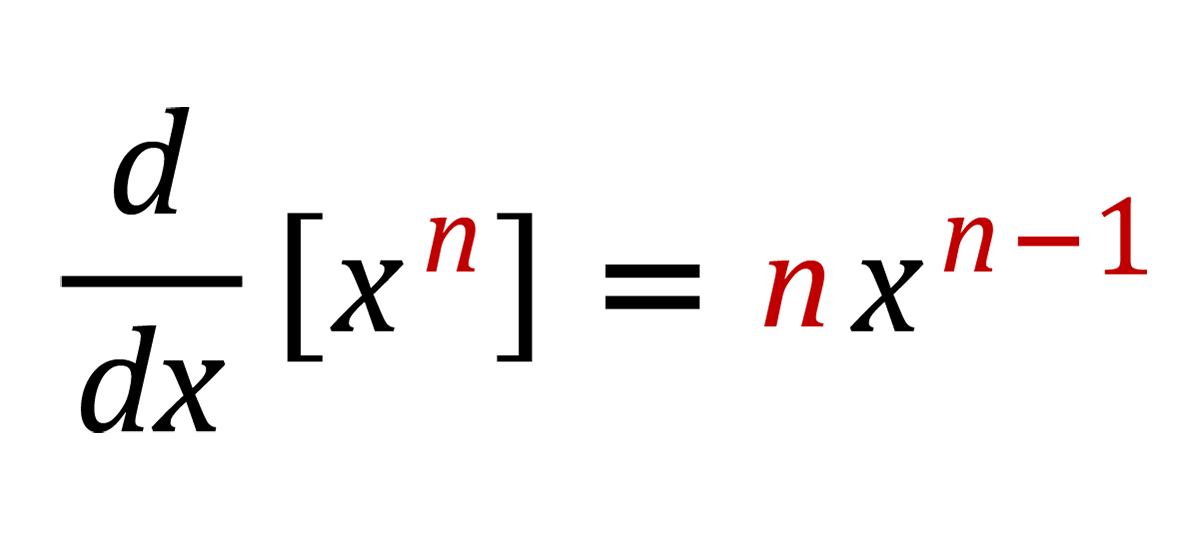
Power Rule

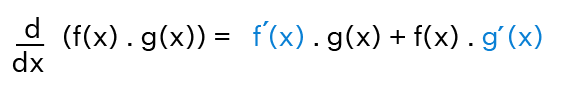
Product Rule

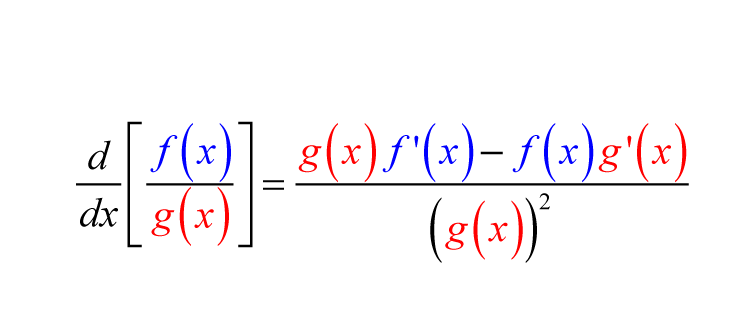
Quotient Rule

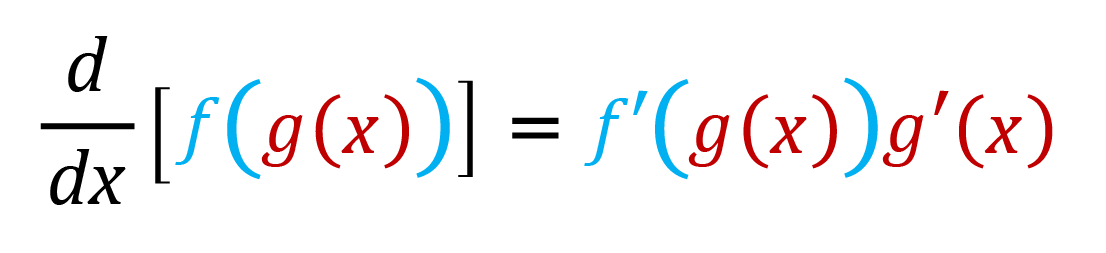
Chain Rule

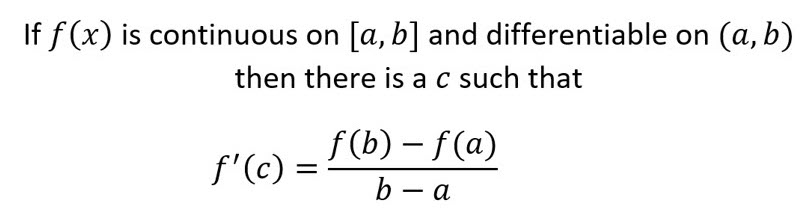
Mean Value Theorem

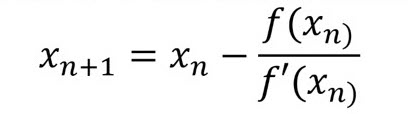
Newton’s Method

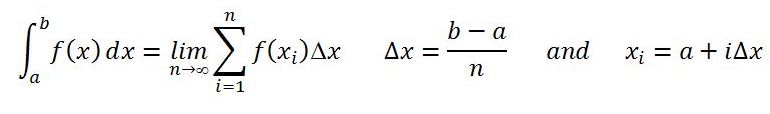
Reiman Sums

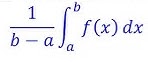
Average Value of a Function

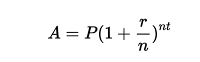
Compound Interest

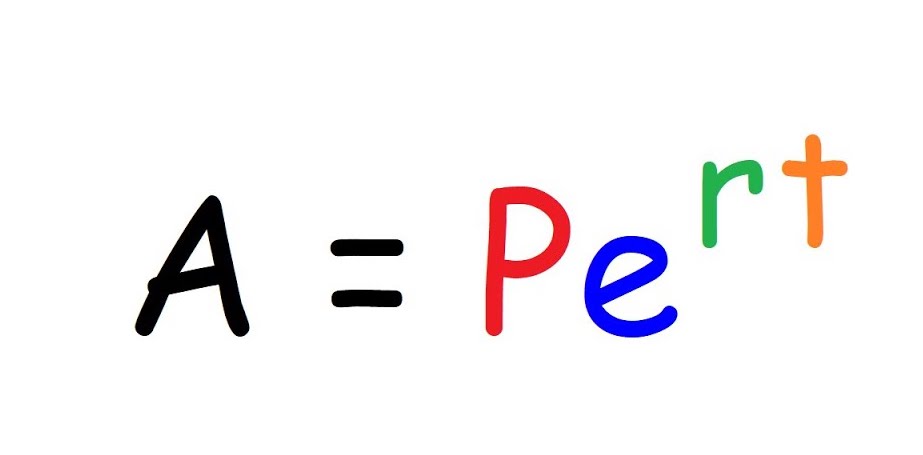
Infinite Compound Interest

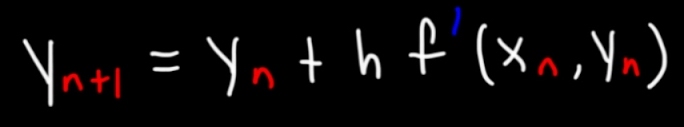
Euler’s Method

The growth of a population grows proportionately to the size of the population

Law of Exponential Growth

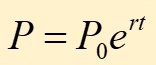
dP/dt = KP

Exponential Growth

dT/dt =K(T-T_o )

T=T_s + (T_o - T_s )e^kt

Newton’s Law of Cooling

dP/dt = KP (1-P/L)

L= Carrying Capacity

P=L/(1+be^-kt ) b= (L-P₀ )/ P₀

Logistics Formula

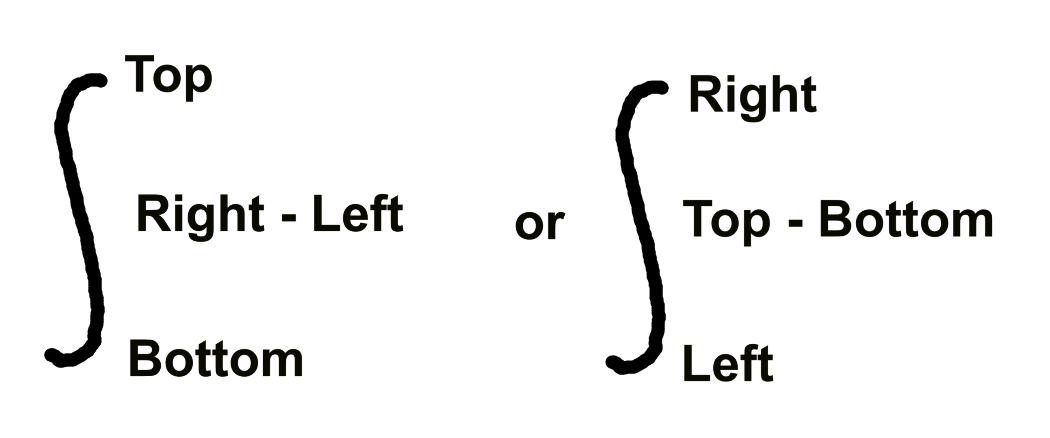
Area Between Curves

Volume

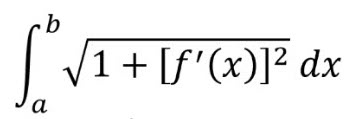
Arc Length

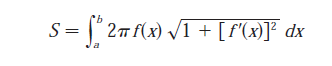
Surface Area

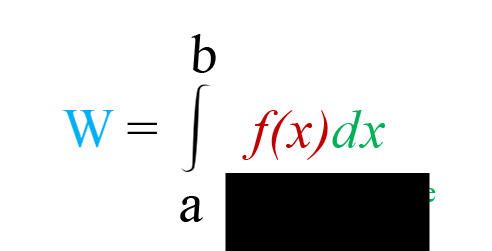
Work

Force= kd

Hooke’s Law

|velocity| =

Speed

Average Rate of Change

Instantaneous rate of change is

a derivative

Derivative of Position

Velocity

Derivative of Velocity

Acceleration

Antiderivative of Velocity

Position

Derivative of cos(x)

-sin(x)

Derivative of sin(x)

cos(x)

Derivative of tan(x)

sec²(x)

Derivative of sec(x)

sec(x)tan(x)

Derivative of csc(x)

-csc(x)cot(x)

Derivative of cot(x)

-csc²(x)

Derivative of y=a^x

a^xln(a)

Derivative of f(x)= log_ax

1/(xln(a))

Derivative of ln(x)

1/x

Derivative of tan^-1(x)

1/(1+x²)

Derivative of sin^-1(x)

1/√(1-x²)

Derivative of sec^-1(x)

1/(x√(x²-1))

Derivative of cot^-1(x)

-1/(1+x²)

Derivative of cos^-1(x)

-1/√(1-x²)

Derivative of csc^-1(x)

-1/(x√(x²-1))

∫cos(x)dx

sin(x)+c

∫sin(x)dx

-cos(x)+c

∫tan(x)dx

-ln|cos(x)|+c

∫cot(x)dx

ln|sin(x)|+c

∫sec(x)dx

ln|sec(x)+tan(x)|+c

∫csc(x)dx

-ln|csc(x)+cot(x)|+c

∫a^xdx

a^x/ln(a) +c

∫1/√(a²-x²)dx

sin^-1(x/a) +c

∫1/(a²+x²)dx

1/a tan^-1(x/a) +c

∫1/√(a²-x²)dx

1/a sec^-1(|x|/a) +c

sin²(x)+cos²(x)=1

1+tan²(x)=sec²(x)

1+cot²(x)=csc²(x)

Pythagorean Identities

sin(x)=1/csc(x)

cos(x)=1/sec(x)

tan(x)=1/cot(x)

csc(x)=1/sin(x)

sec(x)=1/cos(x)

cot(x)=1/tan(x)

Reciprocal Identities

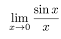
=1

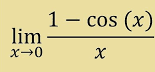
=0

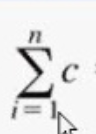
Summation Formula

cn where c is a constant

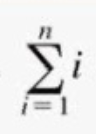
Summation Formula

n(n+1) / 2

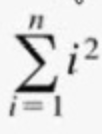
Summation Formula

n(n+1)(2n+1) / 6

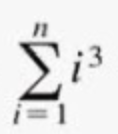
Summation Formula

n²(n+1)² / 4

Let f be continuous on [a,b] and let n be an EVEN integer. ∫^b_a f(x) dx is:

∫^b_a f(x) dx ≈ b-a / 3n [ f(x₀) + 4(f(x₁)) + 2(f(x₂) + 4(f(x₃) + … + 4(f(x_n-1) + f(x_n)

Simpson’s Method

2π∫^b_a radius (f(x)) dx

Shell method formula

∫u dv = uv - ∫v du

Integration by Parts Formula

Trigonometric Integrals:

If the degree of a sinx is odd…

break one sinx off to save it for a “u” substitution

Trigonometric Integrals:

If the degree of a cosx is odd…

break off a cosx to save it for a substitution

Trigonometric Integrals:

When both the sinx and the cosx are even…

repeatedly use the properties:

sin²x = 1-cos2x / 2 and cos²x = 1+cos2x / 2

Trigonometric Integrals:

If the secx is even…

break off a sec²x to save for substitution

Trigonometric Integrals:

If tanx is odd…

break off both a secx and a tanx

Trigonometric Integrals:

When there is just a tanx…

break off a tan²x

Trigonometric Integrals:

If there is just an odd secx…

do an integration by parts

Trigonometric Integrals:

If a secx tanx problem can’t be solved…

try doing it in cosx sinx

Trigonometric Substitution

√a²-x²

x= asinu

Trigonometric Substitution

√a²+x²

x = atanu

Trigonometric Substitution

√x²-a²

x = asecu

How to solve a partial fractions problem

1. Factor the denominator

2. Split up the denominator into two (or more) fractions added together with A and B as the numerators

3. Multiply by a common denominator

4. Set that equal to the original numerator

5. Solve for A and B

6. Plug into integral and solve

Parametric Equations

dy/dx =

dy/dt / dx/dt

Parametric Equations

d²y/dx² =

d/dt(dy/dt) / dx/dt

Parametric Equations

d³y/dx³ =

d/d(d²y/dx²) / dy/dt

∫_a^bg(t)f’(t) dt

Parametric Equations

Area

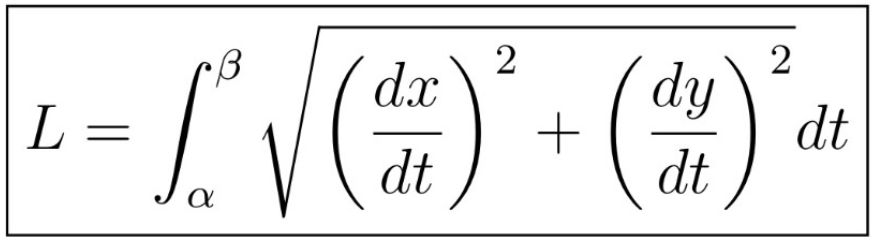
Parametric Equations

Arc Length

|𝑣⃗| =

magnitude (length)

√a²+b²

i vector

<1,0>

j vector

<0,1>

lim_t→a< f(t), g(t) > =

< lim_t→af(t), lim_t→ag(t) >

𝑣⃗ ‘(t) =

< f’(t), g’(t) >

∫_a^b𝑣⃗ dt

< ∫_a^b f(t) dt, ∫_a^b g(t) dt

Speed in Vectors =

Magnitude

Polar to Rectangular

x= rcosθ

y=rsinθ

Rectangular to Polar

tanθ = y/x

r² = x² + y²

In Polar Coordinates

dy/dx =

(f’(θ) * sinθ + f(θ) * cosθ) / (f’(θ) * cosθ - f(θ) * sin*)

½ ∫_a^b (f(θ))² dθ

f(θ) = r

Polar Coordinates

Area

∫_a^b √(f(θ))² + (f’(θ))²

Polar Coordinates

Arc Length

2π ∫_a^b f(θ) * sinθ √(f(θ))² + (f’(θ))²

Polar Coordinates

Surface Area when rotating about the polar (x) axis

2π ∫_a^b f(θ) * cosθ √(f(θ))² + (f’(θ))²

Polar Coordinates

Surface Area when rotating about θ = π/2 (y axis)

∑^∞_n=0 a(r)ⁿ = a / 1-r as long as 0<r<1

Geometric Series

Test for Divergence

Do the limit test and the series is divergent if lim≠0

If f(x) is continuous, positive, and decreasing then ∑^∞_n=1 a_n is convergent if and only if ∫^∞₁ f(n) dn is convergent.

If it is divergent then the series is divergent.

Integral test

Any power greater than 1 is convergent.

Any power less than 1 is divergent

P-series test