Ultimate Knowt Guide: AP Physics C, 2023

Vectors

These specify the magnitude and direction.

Scalars

These specify the magnitude and no direction.

Speed

indicates how fast an object is moving but not in what direction.

Velocity

indicates both how fast an object is moving and in what direction.

arrow

A vector is generally represented by an \_____ whose direction is in the direction of the vector and whose length is proportional to the vector’s magnitude.

positive

To multiply a vector by a \_________ scalar , simply multiply the vector’s magnitude by the scalar.

negative

To multiply a vector by a \________ scalar , change the vector’s magnitude and reverse the direction of the vector.

Speed

Indicates how fast an object is moving but not in what direction.

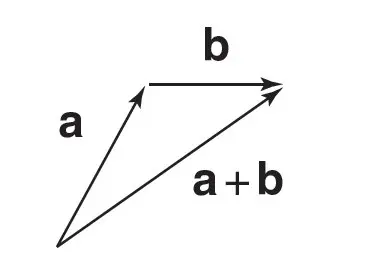
Vector Addition

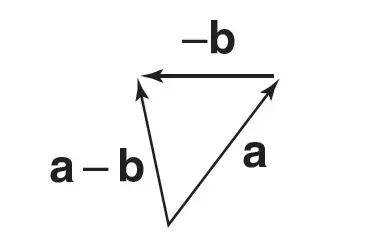
Vector Subtraction

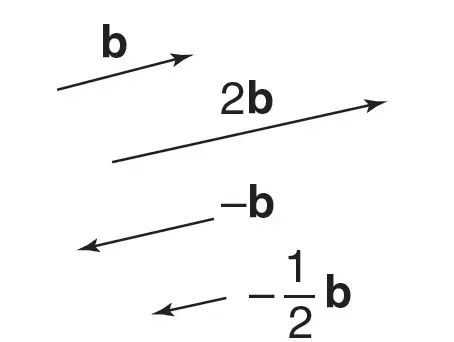
Scalar Multiplication

perpendicular

If two vectors are \________ , their dot product will equal zero [cos(π/2) \= 0].

parallel

If two vectors are \_______ , their dot product will equal the product of their magnitudes (cos 0 \= 1).

antiparallel

If two vectors are \_________ , their dot product will be the negative of the product of their magnitudes [cos(π) \= −1].

Scalar Product

Dot product is also known as?

third

The cross product of two vectors yields a \____ vector.

Vector Product

Cross product is also known as?

units

All measurements and observable quantities have \________; otherwise they would be meaningless.

Multiplication and division

Units are multiplied and divided just as variables are.

Addition and subtraction

The sum or difference of two quantities with the same units has those same units.

Exponential function

The argument x of an \__________, such as ex, must be dimensionless, such as the ratio of two lengths.

dimensionless

Arguments of trigonometric functions, such as sinx and tan−1x , also must be \___________

Velocity

Indicates both how fast an object is moving and in what direction.

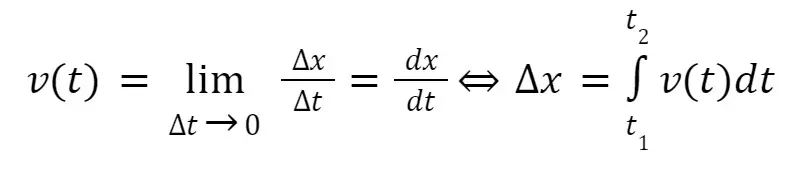
Instantaneous velocity (2D Kinematics)

Instantaneous speed

The magnitude of instantaneous velocity.

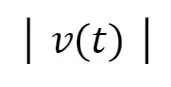
Instantaneous speed (2D Kinematics)

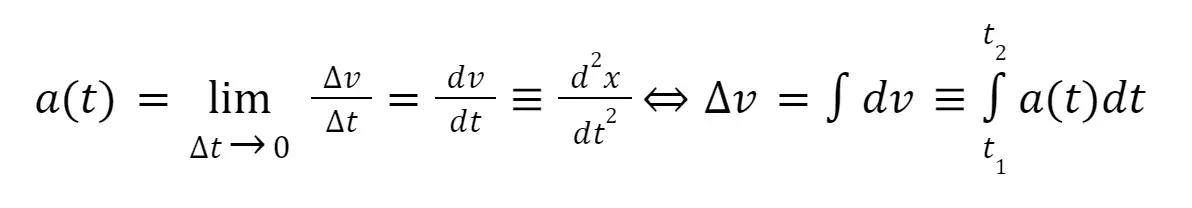
Instantaneous acceleration (2D Kinematics)

Displacement

The net difference in the location of an object independent of how the object got there.

Average quantities

These are often denoted as the variable with a bar over it (v, a)

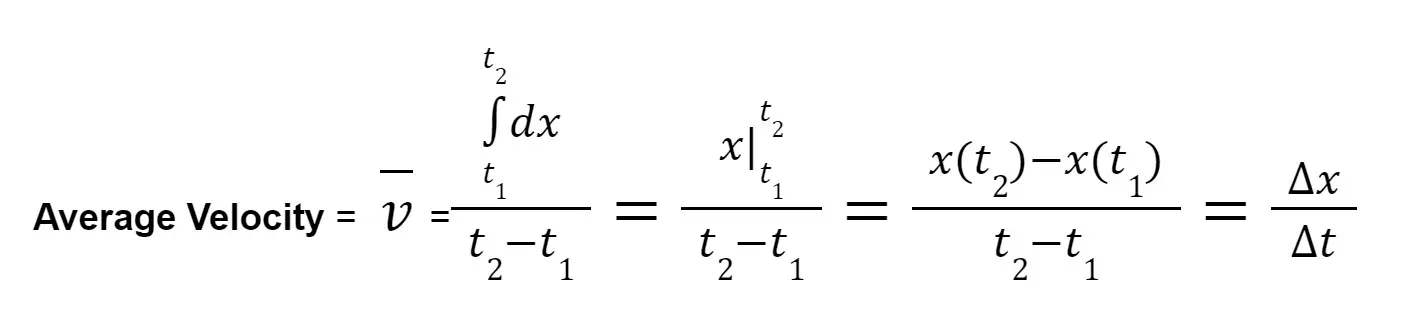
Derivation of Average Velocity

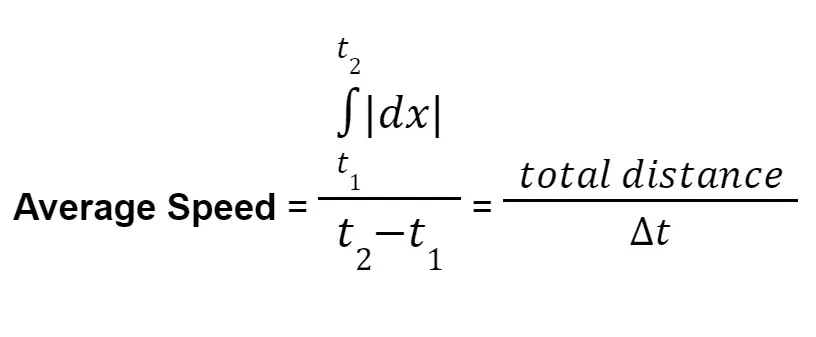
Derivation of Average Speed

Total Distance

The distance traveled irrespective of direction

vectors

Velocities and displacements are \__________

scalars

speeds and distances are \_________

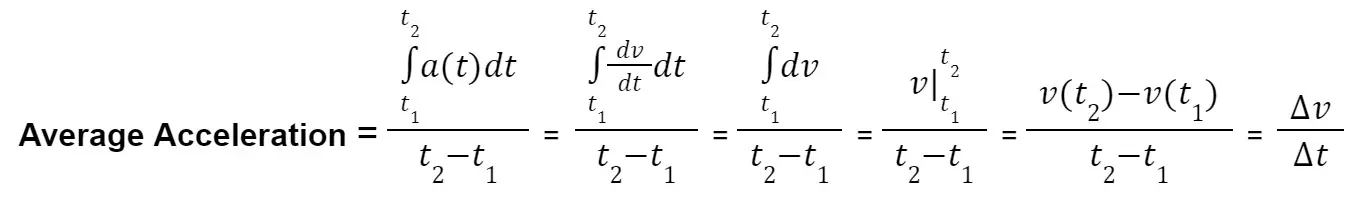
Derivation of Average Acceleration

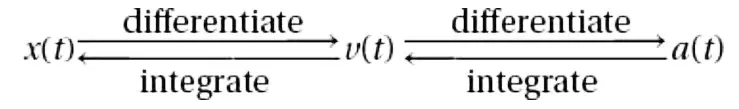
fundamental schematic

positive curvature

Positive acceleration corresponds to \____________

negative curvature

Negative acceleration corresponds to \_________

Non Uniform accelerated motion problems

These generally involve conversion between position, velocity, and acceleration via differentiation or integration .

UAM problems

These problems give you a set of values (such as x0, v0, a, t1, and t2) and ask you to calculate other values from them.

position vector

A natural way to describe the position of an object in more than one dimension is to define a \_______ that points from the origin to the location of the object.

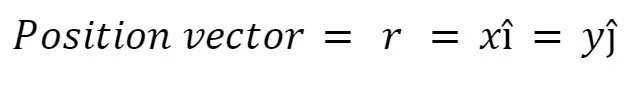
Position Vector Definiton

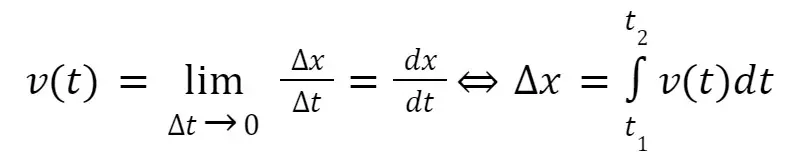
Instantaneous velocity (2D Kinematics)

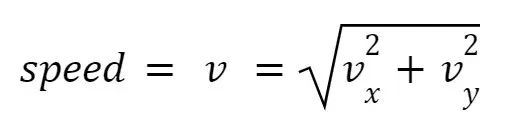
Instantaneous speed (2D Kinematics)

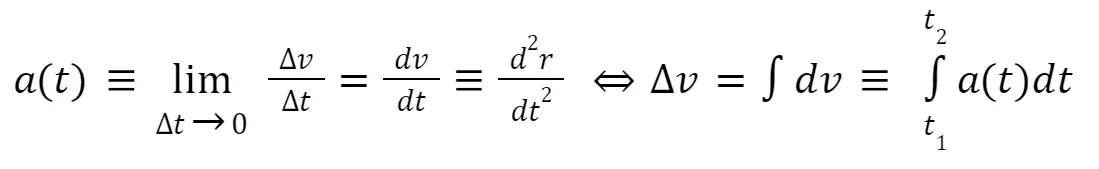
Instantaneous acceleration (2D Kinematics)

two-dimensional vector equations

The definitions of velocity and acceleration are \____________ , each of which is equivalent to a set of two one-dimensional equations.

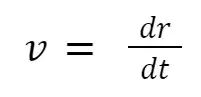
definition of velocity

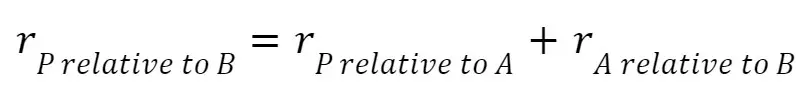
Vector addition relates the position of an object relative to two different frames of reference

Tangential Acceleration (a∥)

Affects only the magnitude of the velocity vector.

Radial Acceleration  (a⊥)

Affects only the direction of the velocity vector.

ω

determines the sense of rotation

magnitude of ω

determines how quickly the r(t) vector rotates.

Phase shift angle (ϕ)

A parameter that determines the initial angle and thus the initial position.

Nonuniform circular motion

Refers to motion in a circular path with nonconstant velocity.

Newton’s First Law

When the net force acting on a body is zero, its acceleration must be zero, meaning that the velocity remains constant.

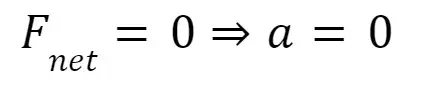
Newton’s First Law

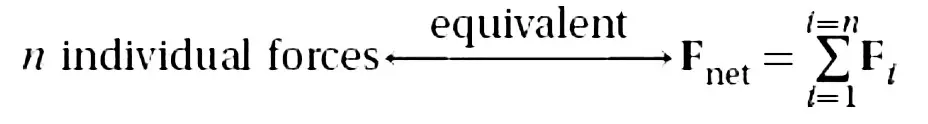
Superposition of Forces

Inertia

It refers to how much an object resists a change in its velocity and is measured by mass.

Newton’s Second Law

This law reveals that force is a vector parallel to the acceleration.

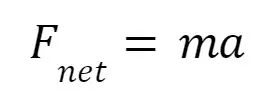
Newton’s Second Law

pounds or newtons

Force is measured in \____________.

Newton’s Third law

For every force exerted by one object on another, there is another force equal in magnitude and opposite in direction that is exerted back by the second object on the first.

Mass

A measure of inertia and is the proportionality constant that relates force to acceleration in Newton’s second law.

Kilograms

SI Unit of Mass

Weight

The magnitude of the force exerted on an object by the closest nearby planet (typically Earth) according to the formula.

Gravitational Force

The most prevalent force in the universe, pulling together on any two objects with mass in the universe.

Normal Force

Denotes FN. Its magnitude is determined by Newton’s second law. Always perpendicular.

Frictional Force

Force that resists the sliding or rolling of one solid object over another.

Static Friction

Objects are not sliding relative to each other.

Static Friction

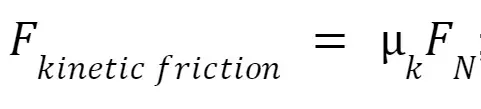
Kinetic Friction

Kinetic Friction

Objects are sliding relative to each other.

Tension Force

A force that develops in a rope, thread, or cable as it is stretched under an applied force.

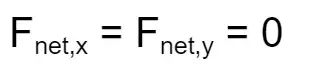
Static equilibrium (object at rest)

centripetal force

The \_________ is the net force required for circular motion . It can be provided by any number of forces such as tension, normal force, gravity, or friction.

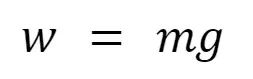
Weight formula

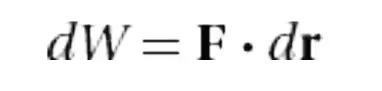
Work by One Force

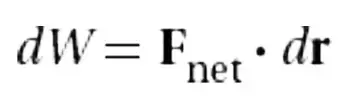
Work due to multiple forces

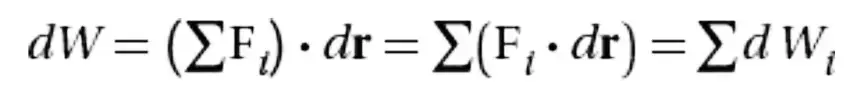
Work due to multiple forces expanded

Joule

The unit of work and energy

Work

the change in an object’s kinetic energy due to the action of a given force.

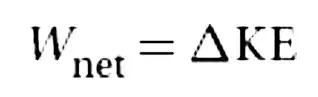
Work–kinetic energy theorem

Work–kinetic energy theorem

This is the first and most fundamental of a number of equations we will soon derive relating various types of work and energy. This theorem is a restatement of Newton’s laws, and it is always valid.

Energy

never created or destroyed; it merely changes form.

Conservative forces

Are involved in reversible energy conversions, where we can get our kinetic energy back.

Nonconservative forces

Are involved in irreversible energy conversions; though the total energy is always conserved, energy is converted to forms from which we cannot recover

Conservative forces

kinetic energy ⇒ potential energy ⇒ kinetic energy

Nonconservative forces

kinetic energy ⇒ sound, heat, etc. ⇒ cannot be easily recovered

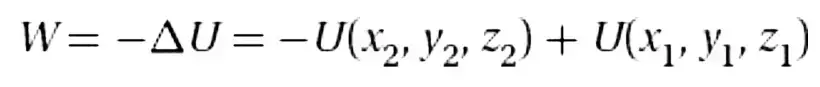
General definition of a potential energy function

Gravitational potential energy

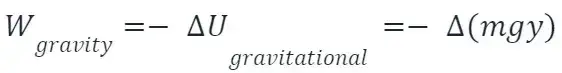
Work done by gravitational force

spring constant

The proportionality constant k , called the \_____________ or force constant, is a property of the particular spring.

negative

The direction of the spring force is opposite the displacement, as indicated by the \______ sign.

restoring force

Because the force always tries to restore the spring to its relaxed state, whether it has been stretched or compressed, it is called a \_______________ .

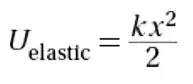
Elastic Potential Energy

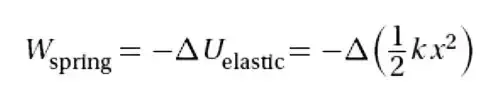
Work Done by Spring Force

general form of the energy conservation equation

Power

The rate at which a force does work on a system

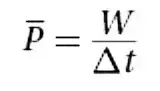
Average power

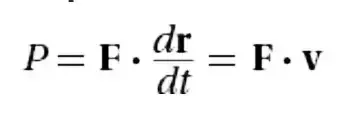
Constant power