GEOMETRY - UNIT 2

- conjunction & disjunction - conditional, converse, inverse, contrapositive - law of detachment & law of syllogism - properties of equality - properties of congruence @izzymosqq

p ∧ q

• joined by the word “and”

• written as “p and q'“

• true when both statements are true

p ∨ q

• joined by the word “or”

• written as “p or q”

• true when at least one of the statements are true

conjunction example ( p ∧ q )

• p: there’s 7 days in a week

• q: march has exactly 30 days

ANSWER:

• there’s 7 days in a week and march has exactly 30 days.

  • truth value: false; march has 31 days

disjunction example ( p ∨ q )

• p: there’s 7 days in a week

• q: march has exactly 30 days

ANSWER:

• there’s 7 days in a week or march has exactly 30 days.

  • truth value: true

conditional statement ( p 🠒 q )

• read as “if p, then q”

• written using “if, then” form

inverse statement ( ~ p 🠒 ~ q )

• formed by negating p (hypothesis) & q (conclusion)

converse statement ( q 🠒 p )

• formed by switching p (hypothesis) & q (conclusion)

contrapositive statement ( ~ q 🠒 ~ p )

• formed by negating and switching p (hypothesis) & q (conclusion)

conditional statement example ( p 🠒 q )

• p: it’s valentines day

• q: it’s february

ANSWER:

• if it’s valentines day, then it’s february

  • truth value: true

inverse statement example ( ~ p 🠒 ~ q )

• p: it’s valentines day

• q: it’s february

ANSWER:

• if it’s not valentines day, then it’s not february

  • truth value: false; february 13th

converse statement example ( q 🠒 p )

• p: it’s valentines day

• q: it’s february

ANSWER:

• if it’s february, then it’s valentines day

  • truth value: false; february 15th

contrapositive statement example ( ~ q 🠒 ~ p )

• p: it’s valentines day

• q: it’s february

ANSWER:

• if it’s not february, then it’s not valentines day

  • truth value: true

law of detachment

• if the hypothesis is true, then the conclusion is true

law of syllogism

• allows you to draw a conclusion from 2 conditional statements

• conclusion of the first statement is the hypothesis of the second statement

law of detachment example

given: if mark saves $30, then he can buy a new video game. mark saves $30.

conclusion: he can buy the new video game

law of syllogism example

given: if it is saturday, then jake has a baseball tournament. if jake has a baseball tournament, then he will need to pack his lunch.

conclusion: if it is saturday, then he will need to pack his lunch

addition property

if a=b,

then a+c = b+c

subtraction property

if A=B,

then A-C = B-C

multiplication property

if A=B,

then A ⋅ B = B ⋅ C

division property

if A=B,

then A/B = B/C

distributive property

if A(B+C),

then A(B+C) = AB + AC

substitution property

if A=B,

then A may be substituted by b in any expression

reflexive property of =

for any real number A,

A=A (always equals itself)

symmetric property of =

if A=B,

then B=A

transitive property of =

if A=B & B=C,

then A=C

def’n of ≅

if AB ≅ CD,

then CD ≅ AB

def’n of midpoint

if B is the midpoint of AB,

then AB = BC

segment addition postulate

if A, B, and C are collinear points, and B is between A and C,

then AB + BC = AC

def’n of a right angle

• an angle measures 90 degrees if and only if it’s a right angle

m∠ = 90 degrees

def’n of complementary angles

• two angles are complementary if and only if the sum of their measures is 90 degrees

m∠ 52 + m∠ 38 = 90 degrees

def’n of supplementary angles

• two angles are supplementary if and only if the sum of their measures is 180 degrees

m∠ 102 + m∠ 88 = 180 degrees

def’n of an angle bisector

• an angle bisector divides an angle into 2 equal parts

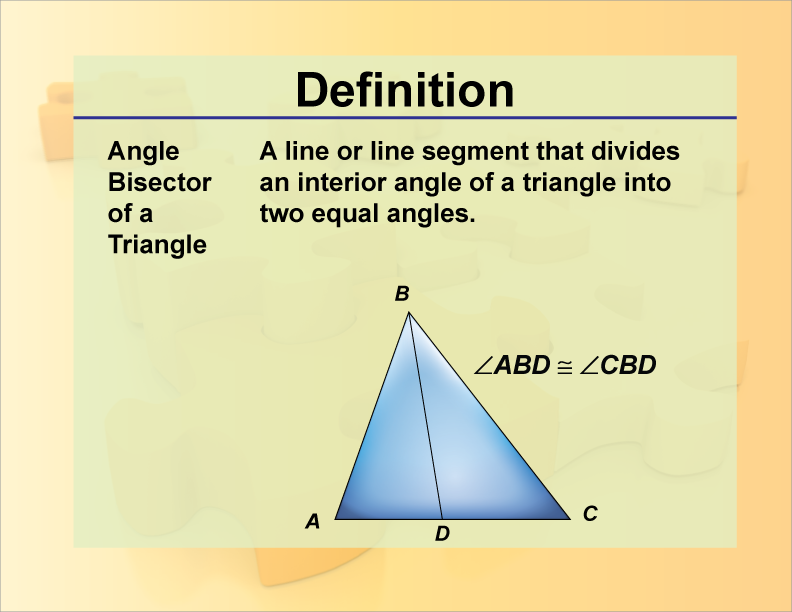
def’n of perpendicular

• perpendicular lines form right angles

angle addition postulate

m∠ ABD + m∠ DBC = m∠ ABC

vertical angles theorem

• if 2 angles are vertical, they they are congruent

complement theorem

• if 2 angles form a right angle, then they are complementary

linear pair theorem (supplement theorem)

if 2 angles form a linear pair, then they are supplementary

congruent complements theorem

• if 2 angles are complementary to the same angle, then they are congruent

if ∠ A is complementary to ∠ B, and ∠ C is complementary to ∠ B,

then ∠ A ≅ ∠ C

congruent supplements theorem

• if 2 angles are supplementary to the same angle, then they are congruent

if ∠ A is supplementary to ∠ B and ∠ C is supplementary to ∠ B,

then ∠ A ≅ ∠ C

∠ 4 = ∠ 5 are supplementary

linear pair theorem

∠ 4 + ∠ 5 = 180

def’n of supplementary angles

m ∠ ABC = 90 degrees

def’n of a right angle

m ∠ 1 + m ∠ 3 = m ∠ ABC

angle addition postulate