Unit 10: Circles

What is the area formula for a circle?

A = πr²

What is the circumference formula for a circle?

C = 2πr

Circle

The set of all points in a plane that are equidistant from a fixed point of the plane called the center of the circle

Radius

A segment from the center of the circle to any point of the dircle

Central angle of a circle

An angle who's vertex is the center of the circle

Arc of a circle

The part of the circle between two points on the circle

Intercepted arc

An arc of a circle if each endpoint of the arc is a different ray of the angle and the other points of the arc and in the interior of the angle

Degree measure of an arc is equal to…

The measure of the central angle that intercepts the arc

Arc length

Measure of the distance along the arc

‘s’ is the symbol for

Arc length

Theta (kinda looks like this ∅) stands for:

The measure of a central angle

The formula for finding arc length is

s/2πr = ∅/360

Chord of a circle

A line segment whose endpoints are points of the circle

Diameter (chord wise)

A chord that has the center of the circle as one of its points

In a circle or congruent circles, two chords are congruent if…

And only if their central angles are congruent

A polygon is inscribed in a circle, and the circle is circumscribed about the polygon, if…

All of the verteces of the polygon are points of a circle

Inscribed angle of a circle

An angle whose vertex is on the circle and whose sides contain chords of the circle

The measure of an inscribed angle of a circle is equal to ___ of the measure of its intercepted arc

1/2

An angle inscribed in a semicircle is a ___ angle

Right - 90°

If two inscribed angles of a circle intercept the same arc, the angles are..

Congruent

If a line is drawn alongside a circle, it could intersect the circle ___ times

0, 1, or 2

Tangent to a circle:

A line in the plane of a circle, intersects at one and only one point

Secant of a circle

A line that intersects the circle at two points

At a given point on a circle, ___ line can be drawn that is tangent to the circle

1 and only 1

A line is tangent to a circle if and only if it is ___ to a radius at its point of ___ in the circle

Perpendicular, intersection

(Theorem) All radii of the same circle are..

congruent

Congruent circles are circles with congruent ___

radii, diameters

Congruent arcs are arcs of the same circle, or of congruent circles that are ___.

equal in measure

(Theorem) A diameter perpendicuar to a ___ bisects the ___ and its ___

chord, chord, arcs

Two chords are ___ from the center of a circle if, and only if, the chords are congruent

equidistant

Tangent segment

A segment of a tangent line, one of whose endpoints is the point of tangency

Tangent segments drawn to a circle from an external point are ___

congruent

If two tangents are drawn to a circle from an ___, then the line segment from the center of the circle to the ___ ____ the angle formed by the tangents, and the angle whose vertex is the center of the circle and whose rays are two tangents drawn to the ___

external point, external point, bisects, point of tangency

A polygon is circumscribed about a circle if each side of the polygon is ___ to the circle

tangent

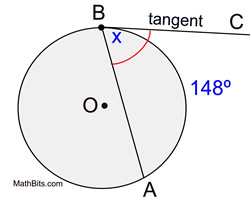
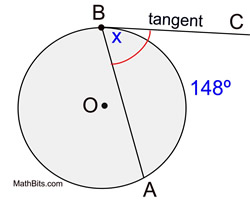
The measure of an angle formed by a ___ & a ___ that intersect at the point of tangency is equal to ½ the measure of the intercepted arc

tangent & chord

m<ABC = 1/2m(arc)AB

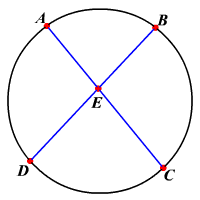
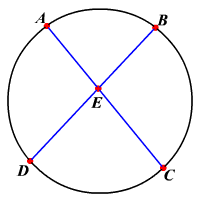
The measure of an angle formed by two chords intersecting within a circle is equal to ½ to sum of the measures of the ___ intersected by the ___ and its ___

arcs, angle, vertical angle

m<AED = 1/2(m(arc)CB + m(arc)AD)

m<AED = m<BAE + m<ABE

(Theorem) The measure of an angle formed by a tangent and a secant, two secants, or two tangents intersecting outside the circle, is equal to ½ the difference of the ______

measures of the intercepted arcs

If 2 secant segments are drawn to a circle from an external point, then the product of the ___ of one secant segment and its external segment is equal to the product of the ___ of the other secant segment and its external segment.

length

What’s the center of the circle represented by? (point)

(h, k)

The equation of the circle with center (h, k) and radius r is

(x - h)² + (y - k)² = r²

What’s the equation of a circle with the center (3, 2) and radius of 5?

(x - 3)² + (y - 2)² = 25

How do you solve this equation using completing the square?

x² - 4x - 7 = 0

x² - 4x = 7

x² - 4x + (-4/2)² = 7 + (-4/2)²

(x - 2)² = 7 + 4

(x - 2)² = 11

x = 2+-√11

How do you find the center and radius of the circle using completing the square?

x² + y² - 2x + 6y - 6 = 0

x² - 2x + y² + 6y = 6

x - 2x + (-2/2)² + y² + 6x + (6/2)² = 6 + (-2/2)² + (6/2)²

(x - 1)² + (y + 3)² = 16

center: (1, -3) radius: r = 4

If two chords intersect within a circle, the ___ of the measures of the segments of one chord is equal to the ___ of the measures of the segments of the other

product

If a tangent and secant are drawn to a circle from an external point, then the square of the length of the ___ segment is equal to the ___ of the lengths of the secant segment and its external segment

tangent, product