7 Forces and energy

what are the 3 dimensions

M - mass

T - time

L - length

[g]

[g] = [a] = LT⁻²

[E]

[E] = [mgh] = ML²T⁻²

= [½mv²] = ML²T⁻²

[k] where k is any constant

no dimensions

Formula for work done

Force x distance

Where the force and distance act in the same direction (parallel)

Formula for work done as force varies with distance (x)

W.d = ∫ F do

Units of work done

Joules of newton meters

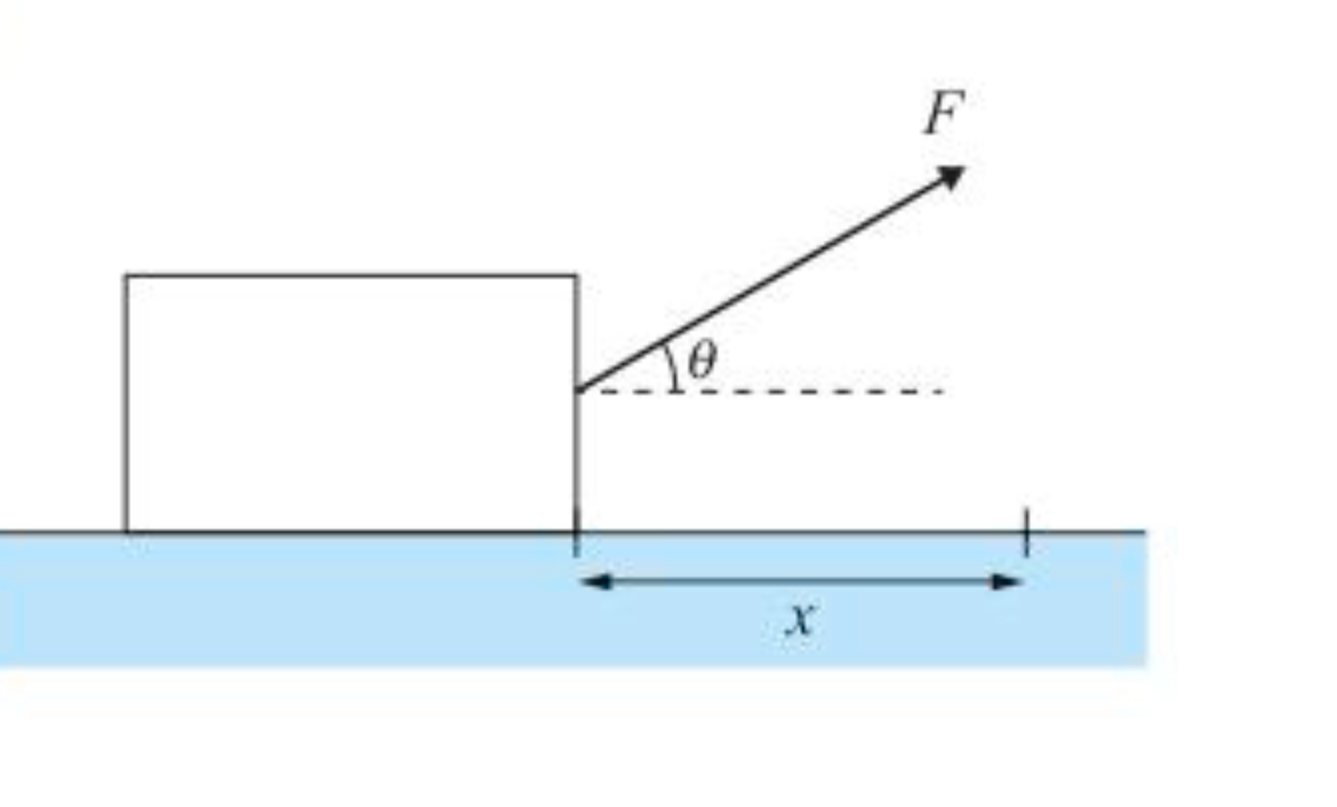
Work done as the block moves x meters

Fcosθ x x

Forces do no work when

The force is perpendicular to the direction of motion

Describe what power is

The rate at which work is done

Formulas for power

= work done / time taken

= force x speed

Instantaneous power

Force x speed

Where speed varies and force is the driving force only

Units of power

Watts(w) or Joules per second (Js⁻¹)

Conservation of energy with GPE, KE, driving force and resistive forces

GPE₁. + KE₁ + WD by driving force - WD against resistive forces = GPE₂ + KE₂

Kinetic energy =

½ m v²

GPE =

meh

Where h is the vertical displacement

What is true at max speed

Driving force = resistive force

Key assumption when modelling a string as light and elastic

Assume it is not stretched beyond it’s elastic limit

Formula for tension

λx/L

λ - modulus of elasticity measured in newtons

x = extension or compression

L = natural length

EPE =

λx²/2L

(Integral of tension)

What do you need to remember for elastic strings

Strings cannot be extended