All of 3.1 Motion

Define stopping distance

Total distance travelled from when the driver spots the hazard until the driver completely stops the vehicle

What is the equation for stopping distance?

Stopping distance = thinking distance + braking distance

Define thinking distance

Distance travelled between the moment the hazard is spotted until the moment the driver applied the brakes

What is the equation for thinking distance?

s = ut

s = thinking distance, m

u = initial velocity, ms^-1

t = reaction time, s

What factors affect thinking distance?

Alcohol/drugs

Tiredness

Vision/visibility

Music/distractions

Caffeine

Initial speed

Define braking distance?

Distance travelled between the moment the brakes are applied until the moment the vehicle stops

How do you workout braking distance?

u² / 2a

u = initial velocity, ms^-1

a = deceleration, ms^-2

What affects braking distance?

Weather conditions

Road conditions

Heavy load

Tyre traction/bald tyres

Damaged brakes

Initial speed

Define a projectile

An object thrown at an angle to the horizontal

Describe everything you know about projectile motion

The projectile travels in 2 planes, vertical and horizontal which means we needs 2 SUVATs.

Time is the same in both planes since we assume air resistance is negligible.

Describe everything you know about vertical motion

Acceleration is due to gravity, a = g = 9.81^-s

Max height is reached when v = 0

Negative acceleration = deceleration

Time to reach maximum height = time of flight / 2

From/to rest = u/v = 0

Describe everything you know about horizontal motion

No horizontal acceleration, a = 0

Velocity remains constant since there’s no resultant force, u = v

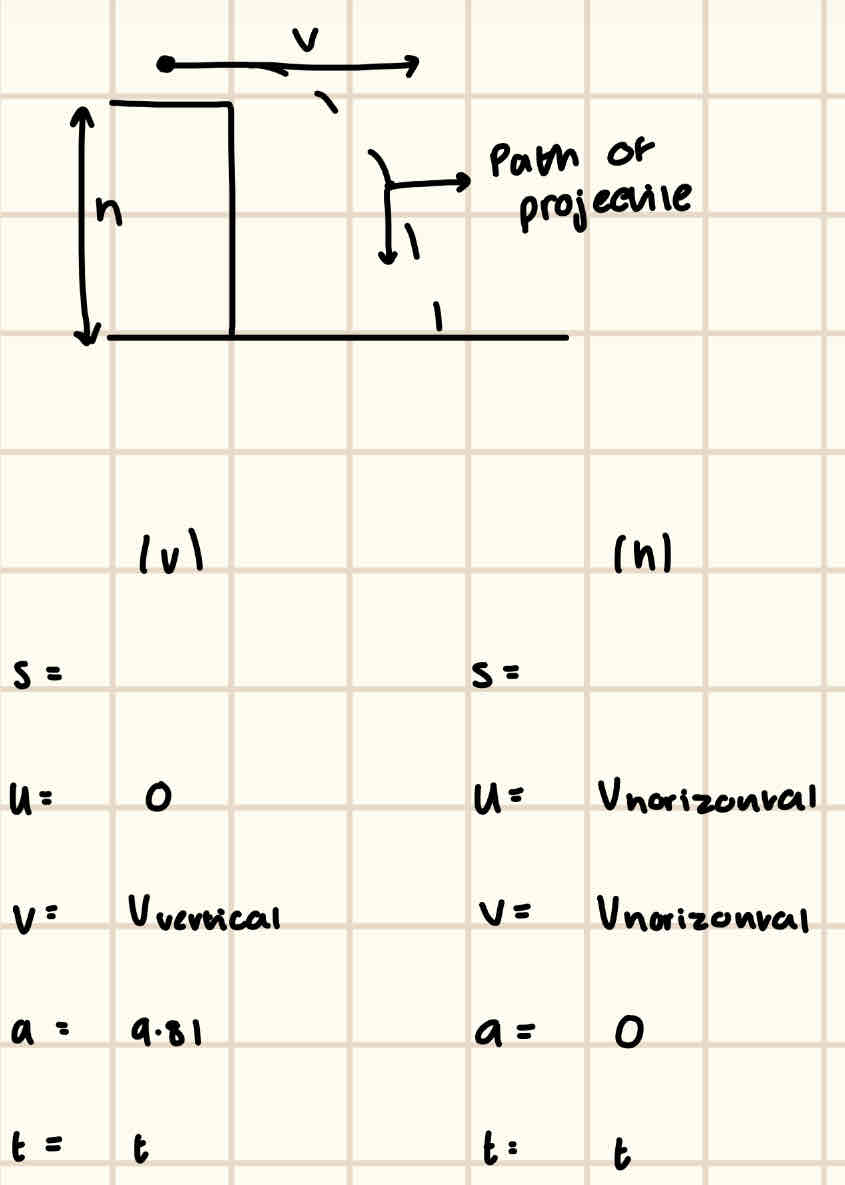
Sketch the 1st model of projectile motion and describe what we need to do to find all missing variables

1) Find the time of flight, t

2a) Find the maximum vertical height, when v = 0

2b) Find the horizontal displacement/range, ONLY after t is found

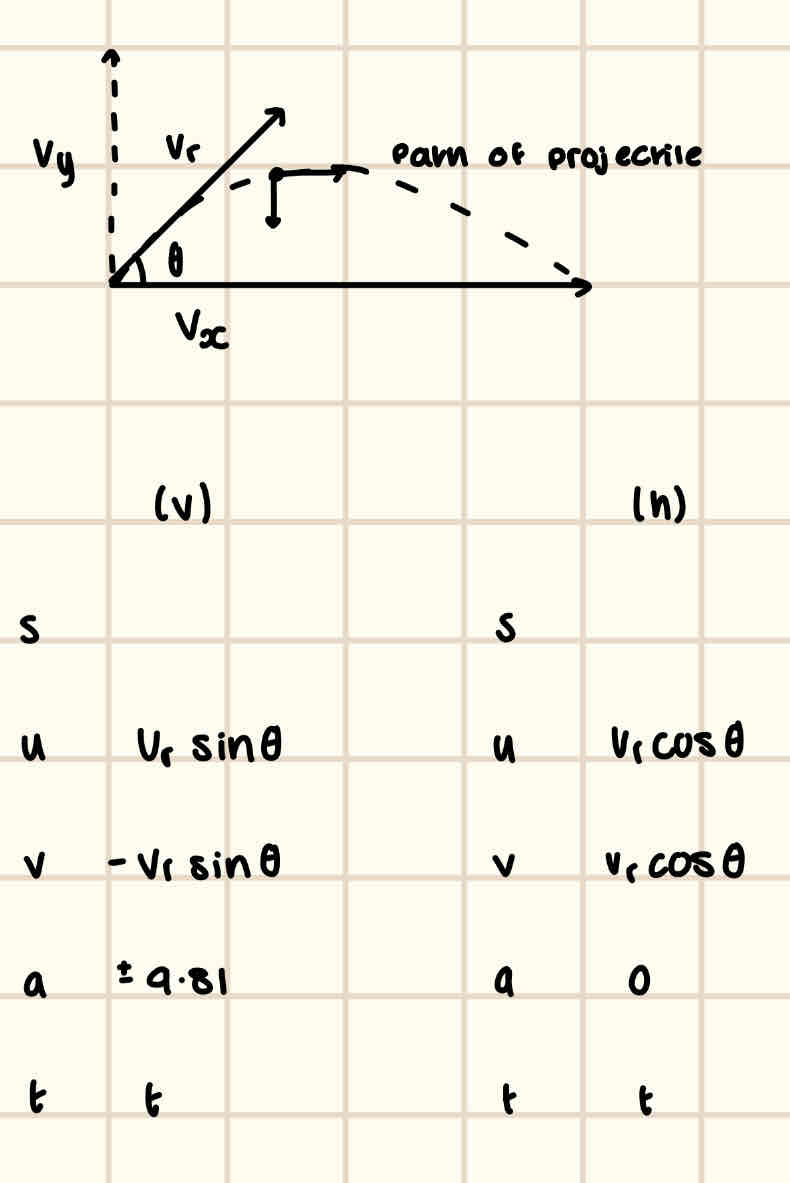
Sketch the 2nd model of projectile motion and describe what we need to do to find all missing variables

1) Find the time of flight, t

2) Find the horizontal displacement/range, ONLY after t is found

3) Find V(v)

What are all the suvat equations?

v = u + at

s = ut + 1/2at²

s = 1/2(u+v)t

v²=u²+2as

s = displacement, m

u = initial velocity, ms^-1

v = final velocity, ms^-1

a = acceleration, ms^-2

t = time, s

What graph are all suvat equations derived from?

This velocity time graph

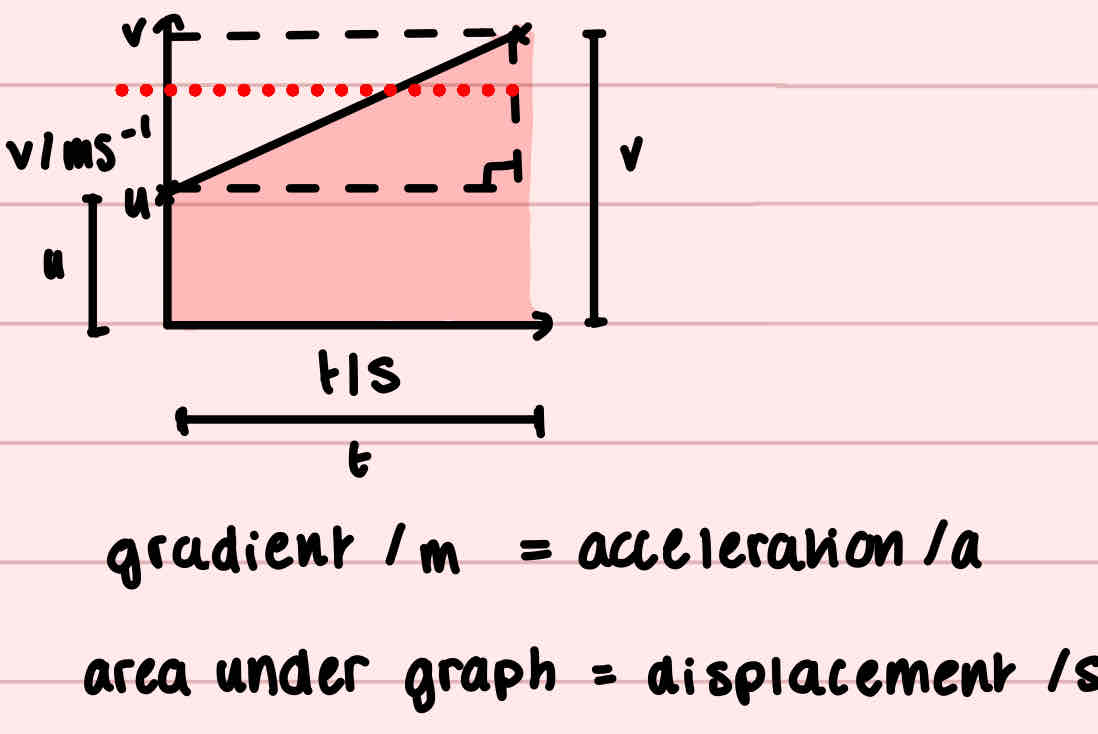
How is the equation without s derived?

Gradient

a = Δv / Δt = v - u / t, xt, +u

v = u + at

How is the equation without v derived?

Area under graph (rectangle and triangle)

Rectangle area = ut

Triangle area = ½ (v-u)t

v = u + at

s = ut + ½ at²

How is the equation without a derived?

Area under graph (trapezium)

½ (a+b)h

½ (u+v)t

How is the equation without t derived?

t = (v - u) / a

s = ½ (v+u) x (v - u) / a x2a

2as = (v+u)(v-u)

v² = u² +2as

What is the acceleration of freefall when an object is falling?

9.81ms^-2

What is the acceleration of freefall/g when an object is rising?

-9.81ms^-2

Define speed, its equation and SI base unit

The rate of change of distance

v = d / t

v = speed, ms^-1

d = distance, m

t = time, s

How is average speed measured?

Work out the speed over a specific time interval

Define distance

The total length covered

Define velocity, its equation and its SI base unit

The rate of change of displacement

v = s / t

v = velocity, ms^-1

s = displacement, m

t = time, s

Define displacement

The distance covered in a given direction

Define acceleration, its equation and SI base unit

The rate of change of velocity

a = v / t

a = acceleration, ms^-2

v = velocity, ms^-1

t = time, s

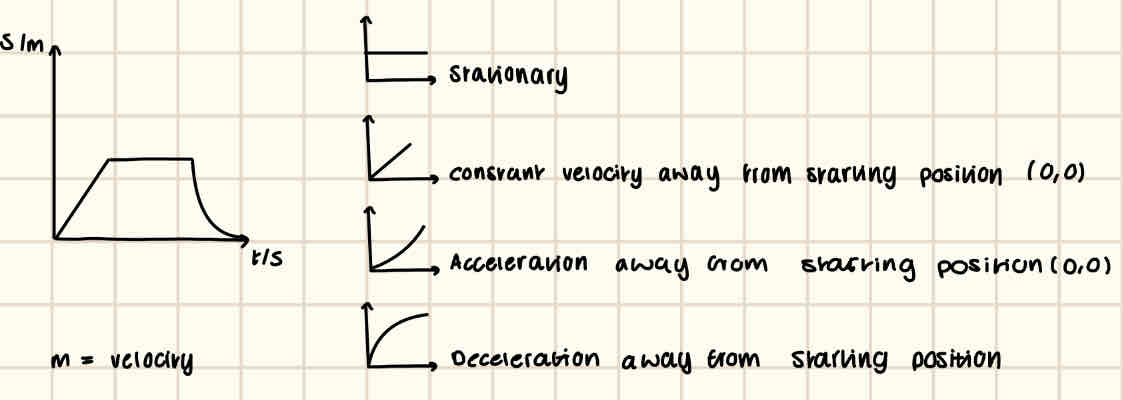
Describe a distance time graph with notes

x axis = time/s

y axis = distance/m

m = speed, ms^-1

The gradient cannot be negative because direction isn’t accounted for.

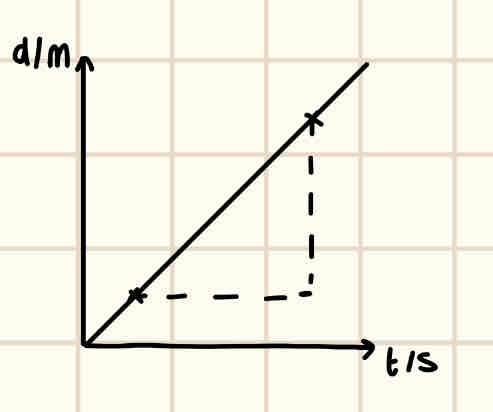
Describe a displacement time graph with notes

x axis = time/s

y axis = displacement/m

m = velocity, ms^-1

The y intercept determines the starting position.

When the gradient becomes positive or negative, it determines whether the object is moving away from/towards the starting position. NOT whether its accelerating or decelerating.

When the gradient increases rapidly then slows down the object is decelerating, when the gradient increases slowly but speeds up rapidly , the object is accelerating.

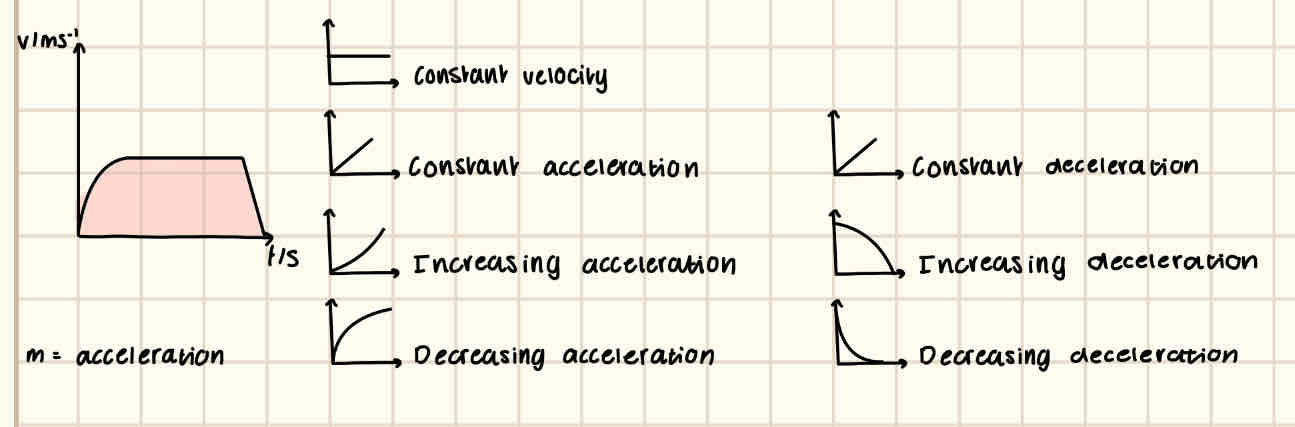
Describe a velocity time graph with notes

x axis = time/s

y axis = velocity/ms^-1

m = acceleration, ms^-2

area under graph = displacement, m

The y intercept determines the stating velocity.

When the gradient becomes positive or negative, it determines whether the object is accelerating or decelerating.

Define instantaneous speed/velocity/acceleration

The speed/velocity/acceleration measured over a very short period of time

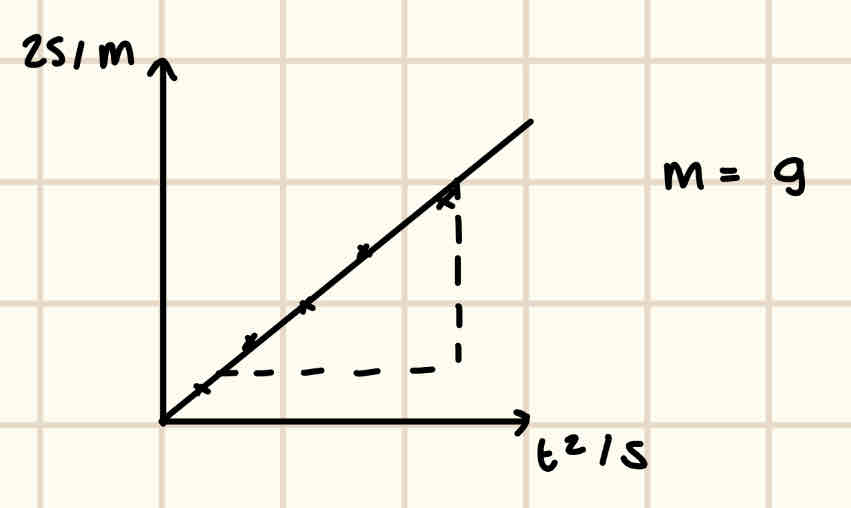
Describe how to determine the acceleration of freefall

We use a trapdoor and electromagnet/light gates, a steel ball bearing and a data logger.

1) A displacement between the trapdoor and electromagnet/light gates is measured with a metre ruler.

2) The steel ball bearing is dropped from rest. We record the time taken for the ball to travel the entire displacement measured on the data logger. This is repeated 3 times to calculate a mean time for this displacement. We repeat the entire process at regular decreasing displacement intervals.

3) We rearrange s = ut + ½ at² to have it in the form y = mx + c where a = g since there’s no external forces acting on the bearing and u = 0 since it’s dropped from rest. We get, 2s = gt².

4) This is the graph:

We draw a line of best fit and the gradient of this line will equal g, m =g