WJEC AS Physics Unit 2.1, 2.2 and 2.3

Unit of charge

Coulomb (C)

The net charge in a system remains constant (provided charges can’t enter or leave)

Electron’s charge

Charge of one electron is a very small fraction of a Coulomb

1.6×10^-19C

Efficiency of a system

% efficiency = useful work (or energy) out/work (or energy) out in

X 100

Conductors

Materials through which a charge can flow

Electricity

The flow of electric charges through a conductor in one direction

Electric current

Base units of current

Cs^-1

Where C = coulombs and s = seconds

Units of current

Amperes (A)

Units of Charge

Coulombs (C)

Charge of electrons

1.6 × 10^-19 C

Number of electrons in 1 amp

Divide by the charge of electrons

Conduction

The result of free electrons which shift towards the higher potential when a voltage is placed across the ends of the wire

n in I=nAve

Number of electrons per unit volume (charge density)

V in I=nAve

Drift velocity

e in I=nAve

Charge of electrons

What current is equal to

Q/t where Q=charge in coulombs and t=time in seconds

Derivation of I=nAve

Potential difference

The pd between two points is the energy converted from electrical potential energy to some other form per coulomb of charge flowing from one point to the other. Unit; V (JC^-1)

What potential difference is also known as

Voltage

How to measure the potential difference in a circuit

Use a voltmeter in parallel

The Volt

Electric resistance

The resistance of a conductor of a conduction is the pd (V) across it divided by the resulting current (I) through it.

R=V/I

Unit; Ω (ohms) = VA^-1

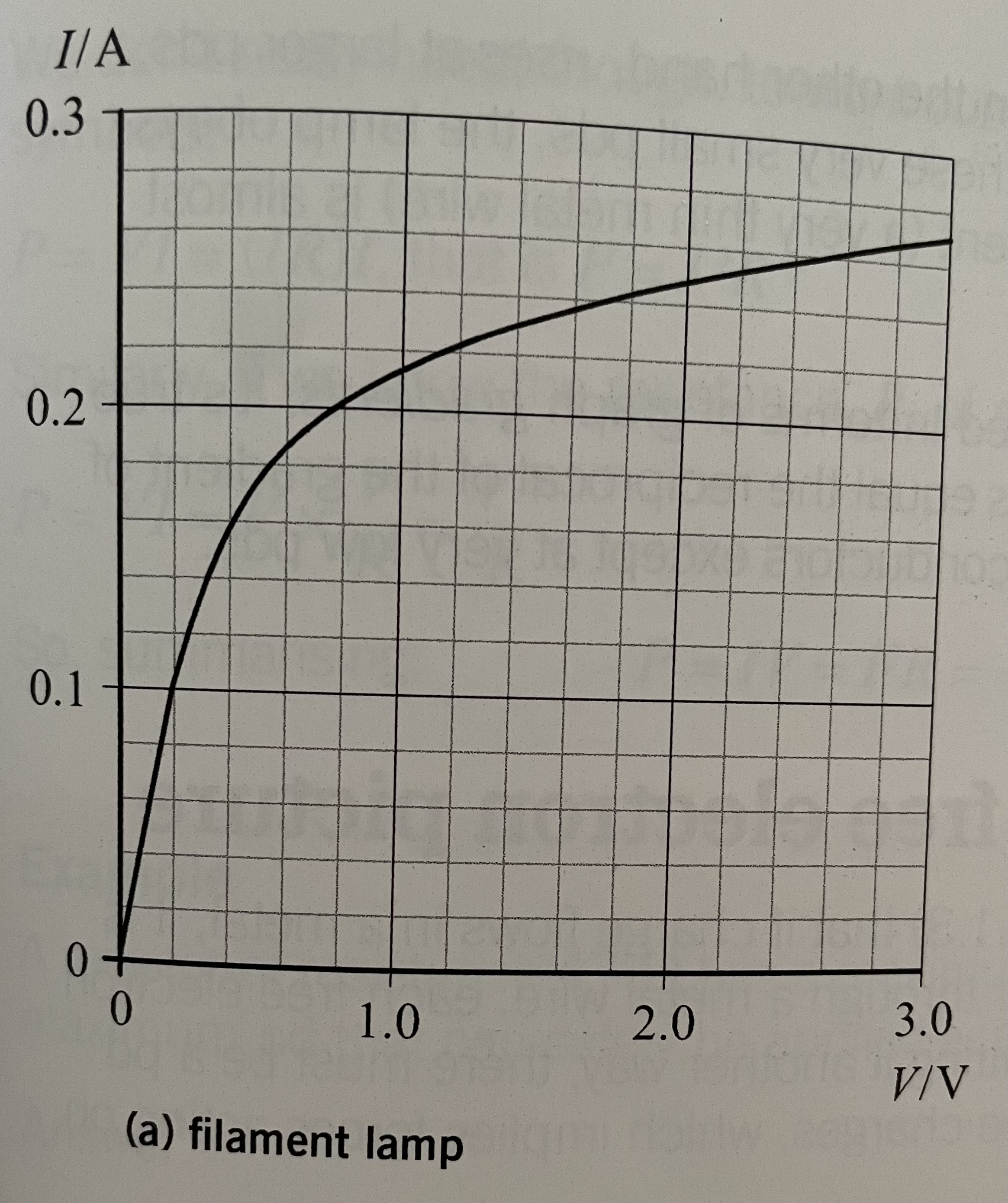
I-V graphs for the filament of a lamp at constant temperature

I-V graphs for a metal wire at constant temperature

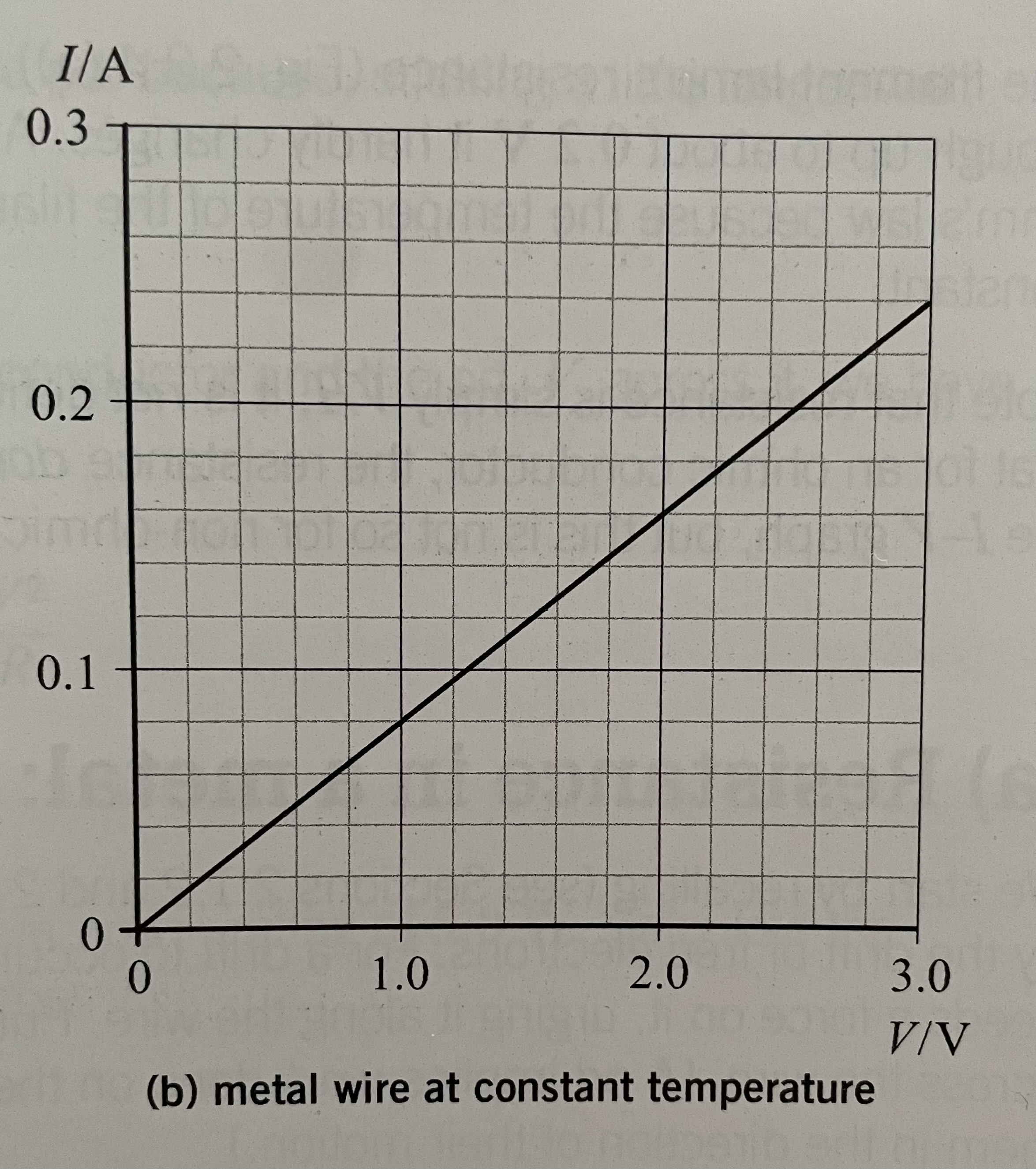
Ohms Law

The current in a metal wire at a constant temperature is proportional to the pd across it

Resistance is equal to

R=V/I

Where; V=voltage and I=current

Units of resistance

Ω (ohms) = VA^-1

Ohmic components

Components that obey Ohm’s law

Non-Ohmic components

Components that don’t obey Ohm’s law

Resistivity, ρ

The resistance, R, of a metal wire of length L and cross-sectional area A is given by R=ρL/A, in which ρ is the resistivity is a constant (at constant temperature) for the material of the wire

Unit ; Ωm

Units of resistivity

Ωm

What reactivity is equal to

RA/L

Where; R=resistance, A=cross-sectional area and L=length of wire

Factors that effect the resistance of a wire

• Length

• Cross-sectional area

• Material

How does cross-sectional area affect resistance of a wire

When the area is doubled, the resistance is halved

How length affect resistance of a wire

Double the length, the resistance doubles

How does material affect resistance of a wire

Resistance is affected by the type of material the wire is made from

Restivity

The resistance, R, of a metal wire of length L and cross-sectional area A is given by R=ρL/A, in which ρ the resistivity, is a constant at a constant temperature for the material of the wire.

Unit; Ωm

Electrical Power

The rate of transfer of electrical potential energy into some other form

The equations for power

P=IV

P=I²R

Where; P=Power, V=Voltage, I=Current and R=Resistance

Deriving the power equations

Superconductivity

Material loses all its electrical resistance below a certain temperature, the superconducting transition temperature. Observed in many metals.

Superconducting transition temperature

The temperature at which a metal, when cooled, loses all its electrical resistance, and becomes super-conducting. Some materials (e.g. copper) never become superconducting however low the temperature becomes

Uses of superconductors

• superconducting wires will carry currents without dissipating any energy at all

• Prototypes of electrical power transmission cables have been set up using ‘high temperature’ conductors. Energy savings

• Electromagnets producing large magnetic fields over large volumes of space use superconducting writes to make coils. MRI

Law of conservation of charge

Electrical charge cannot be created or destroyed, though positive and negative charges can neutralise each other. Charge cannot pile up at a point in a circuit

Current in a parallel circuit

I=I1+I2+I3

Current in a series circuit

I=I1=I2=I3

Potential difference in series circuits

V=V1+V2+V3

Potential difference in parallel circuits

V=V1=V2=V3

Resistance in series circuits

Add the resistances

Resistance in parallel circuits

Add the reciprocals and then reciprocal the product

1/R=1/R1+1/R2+1/R3

Potential divider

A circuit used to pass on a fraction of the input voltage. Consists of a combination of resistors. Uses a series of resistors or variable resistors or components such as a light dependent resistor or thermistor to divide up the potential difference of the source

Uses of potential dividers in circuits

• With LDR

• With thermistor

Circuits containing an LDR and a fixed resistor to form a potential divider

As light level falls, the resistance of the LDR increases, and the voltage increases accordingly (V=IR)

Circuits containing a thermistor and a fixed resistor to form a potential divider

As the temperature level increases, the resistance of the thermistor decreases and then voltage decreases accordingly (V=IR)

emf of a source, E

The emf of a source is the energy converted from some other form (e.g. chemical) to electrical potential energy per coulomb of charge flowing through the source. Unit; V

Internal resistance

The resistance to the flow of current within the source

Current in a circuit containing multiple cells in series

Constant throughout

Potential difference in a circuit containing multiple cells in series

Sum of individual values

Theory of Resistance

In a filament lamp, the resistance increases with temperature. This is because the lattice ions have a greater amplitude (size) of vibration. This causes a greater probability of collisions, causing the frequency of collisions to increase. The average drift velocity increases, hence the resistance increases

1st circuit law

The sum of currents entering a junction is equal to the currents leaving the junction

What the 1st circuit law is due to

The conservation of charge

2nd circuit law

The sum of the p.d.s across the components in a series circuit is equal to the p.d. across the supply

What the 2nd circuit law is due to

The conservation of energy

Constant in a series circuit

Current

Constant in a parallel circuit

Voltage

What a voltmeter reads in an open circuit

E volts (voltage of source)

What EMF can be thought of

The voltage of the source