Gr11-12 Euclidean geometry concepts

Diameter

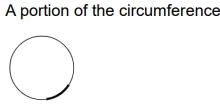
A portion of the circumference

Arc

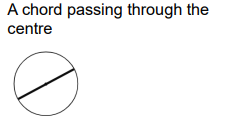
Chord

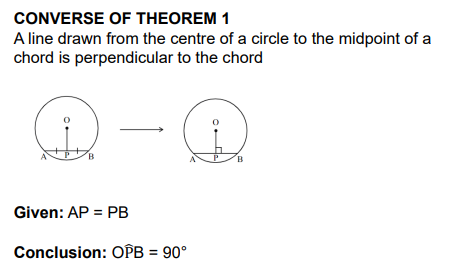
Line from centre perp to the chord

Line from centre to midpt. of chord

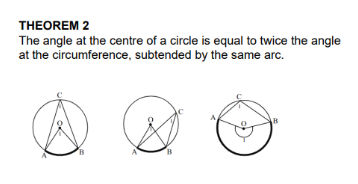
Angle at centre= 2 X angle at circum

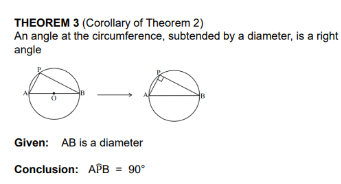
angle in semi circle

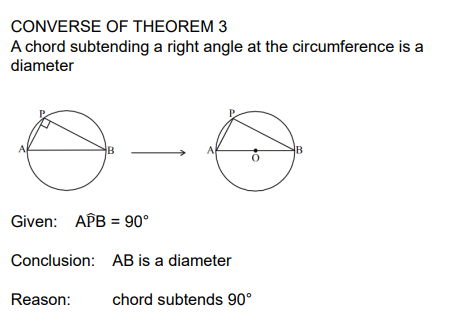
Prove a diameter

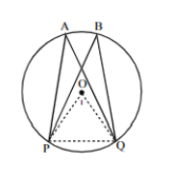
Angles subtended by a chord of the circle, on the same side of the chord are equal

<s in the same seg

Equal chords subtend equal angles at the circumference of the circle.

equal chords; equal angles

Equal chords subtend equal angles at the centre of the circle.

equal chords; equal angles

Equal chords in equal circles subtend equal angles at the circumference of the circles.

equal circles; equal chords; equal angles

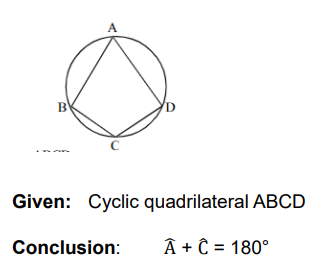
The opposite angles of a cyclic quadrilateral are supplementary

opp angles of cyclic quad

Prove cyclic quad:

If the opposite angles of a quadrilateral are supplementary, then the quadrilateral is cyclic.

opp angles quad supp  OR converse opp angles of cyclic quad

The exterior angle of a cyclic quadrilateral is equal to the interior opposite angle.

ext angles of cyclic quad

Prove cyclic quad:

If the exterior angle of a quadrilateral is equal to the interior opposite angle of the quadrilateral, then the quadrilateral is cyclic.

ext angles = int opp angles OR converse ext angles of cyclic quad

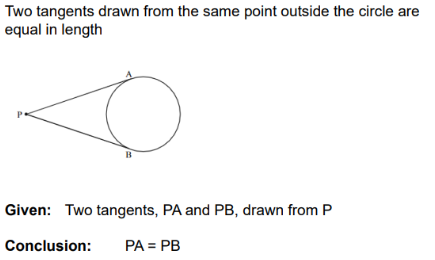
Two tangents drawn to a circle from the same point outside the circle are equal in length

Tans from common pt OR Tans from same pt

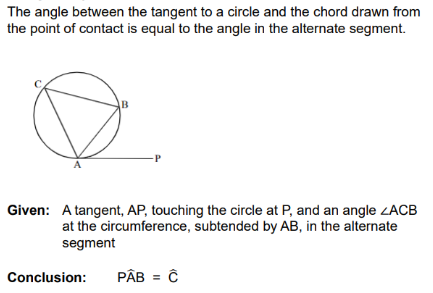
The angle between the tangent to a circle and the chord drawn from the point of contact is equal to the angle in the alternate segment.

tan chord theorem

Prove line is a tangent:

If a line is drawn through the endpoint of a chord, making with the chord an angle equal to an angle in the alternate segment, then the line is a tangent to the circle.

converse tan chord theorem OR angles between line and chord

Prove Line is a tangent

;Line from centre to tangent forms a 90 degree angle

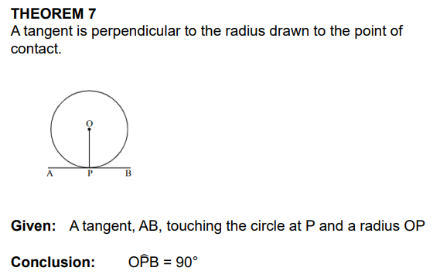
tan perp to radius/diam

Congruent Figures

• Figures that have the same size and shape.

Similar Figures

• Figures that have the same shape but not necessarily the same size.

Equilateral Triangle

• A triangle with all three sides and all three angles equal (each angle is 60 degrees).

The interior angles of a quadrilateral add up to 360°.

sum of angles in quad

The opposite sides of a parallelogram are parallel.

opp sides of parm

Prove a parallogram:

If the opposite sides of a quadrilateral are parallel, then the quadrilateral is a parallelogram.

opp sides of quad are ||

The opposite sides of a parallelogram are equal in length.

opp sides of parm

Prove Parallelogram

If the opposite sides of a quadrilateral are equal , then the quadrilateral is a parallelogram.

opp sides of quad are = OR converse opp sides of a parm

The opposite angles of a parallelogram are equal.

opp angles of parm

Prove parallelogram:

If the opposite angles of a quadrilateral are equal, then the quadrilateral is a parallelogram.

opp angles of quad are = OR converse opp angles of a parm

The diagonals of a parallelogram bisect each other.

diag of parm

Prove parallelogram:

If the diagonals of a quadrilateral bisect each other, then the quadrilateral is a parallelogram.

diags of quad bisect each other OR converse diags of a parm

Prove parallelogram:

If one pair of opposite sides of a quadrilateral are equal and parallel, then the quadrilateral is a parallelogram.

pair of opp sides = and ||

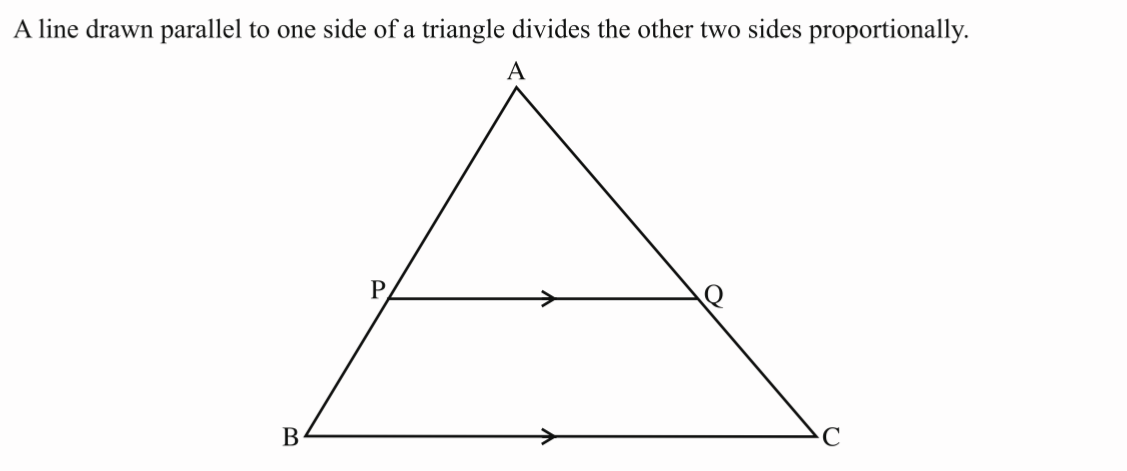
Given 🔺ABC with PQ//BC

Conclusion: AP/PB=AQ/QC - Line // side of 🔺

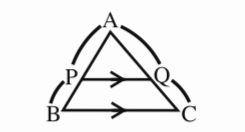
AP/PB=AQ/QC

PB/AP=QC/AQ

What can this ratio also be written as?
AB:BC (m:n)

AB/BC (m/n)

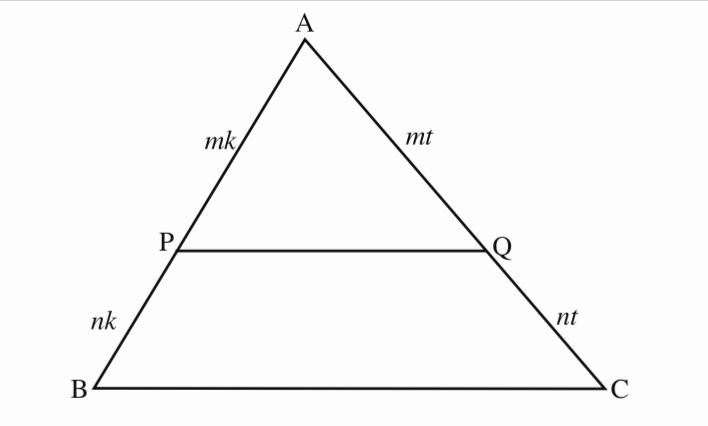
Given: 🔺ABC with AP/PB=AQ/QC

Conclusion: PQ//BC -Line divides 2 sides of 🔺 in prop

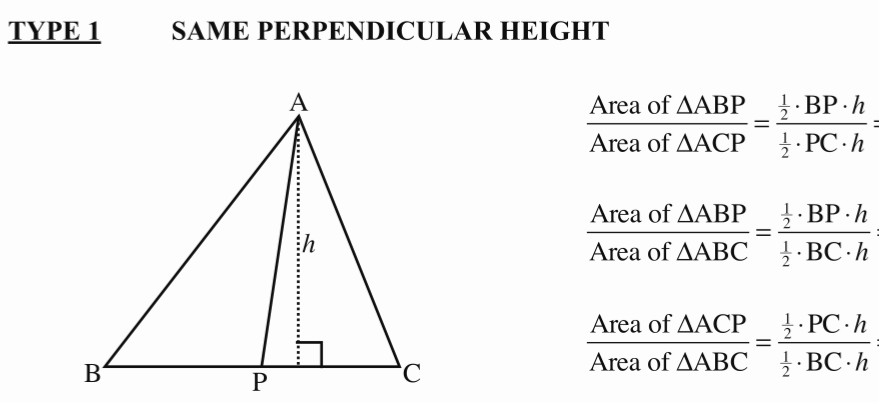
Same perp height

Ratio of areas=Ratio of bases

Common angle; parallel lines

Ratio of areas=(Ratio of corresponding sides)²

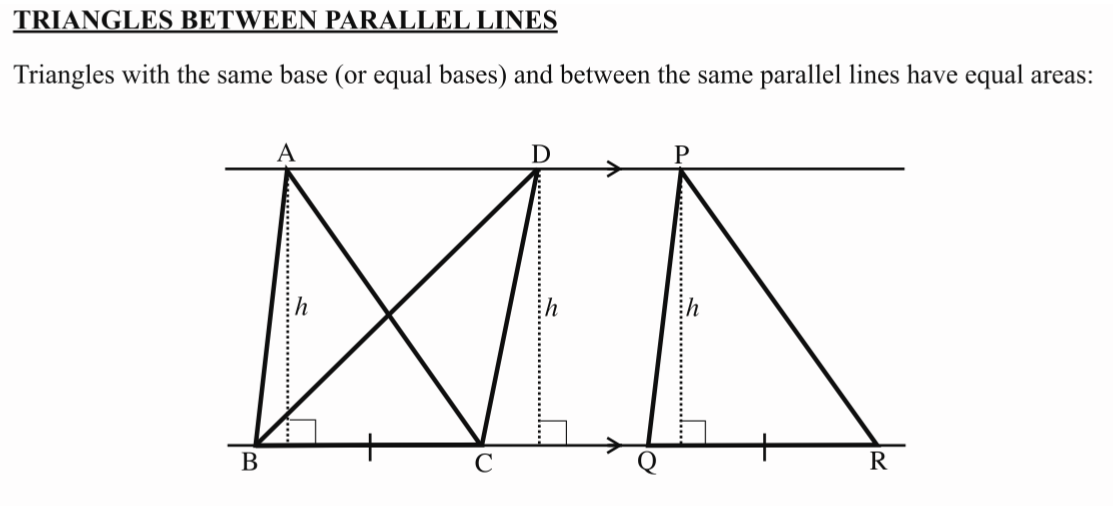
Area of 🔺ABC= Area of 🔺DBC=Area🔺PQR

same base;same height

🔺CAT///🔺DOG

C=D
A=O
T=G

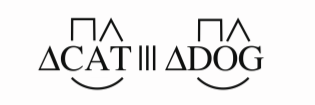
Ratio of the sides are equal

CA/DO = CT/DG = AT/OG

IF TRIANGLES ARE SIMILAR THEIR SIDES ARE?

IN PROPORTION

If you are given: AB/AC =BC/CD and you should prove this..you need to find the triangle first… what two methods can you use?

1. Are the top/bottom of the fraction able to create a reasonable triangle

   1. Are the left/right sides of the fraction able to create a reasonable triangle

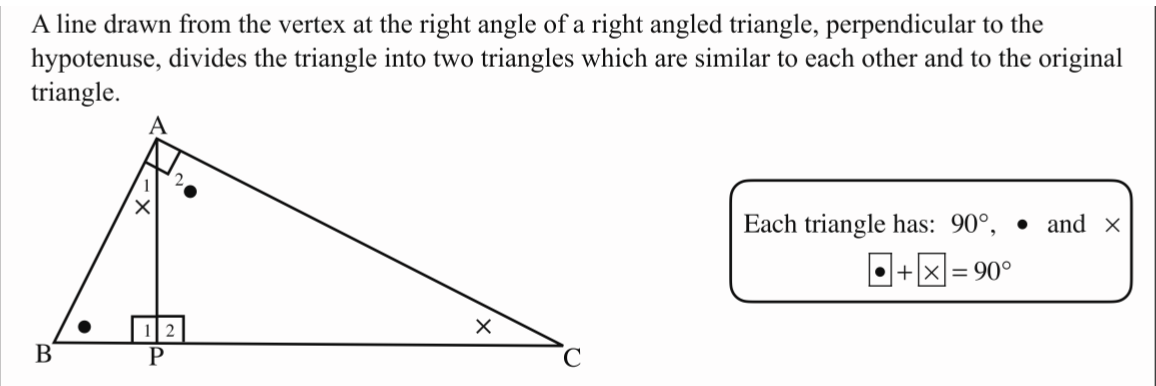
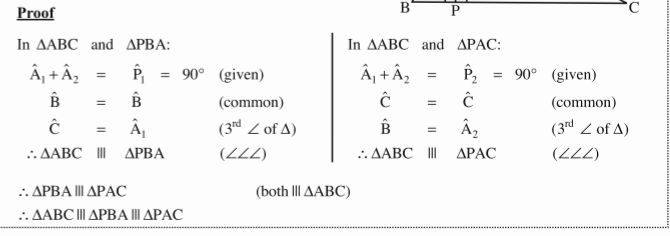
Theorem 3: 🔺ABC///🔺PBA///🔺PAC

reason: Line from right angle vertex perp hypotenuse

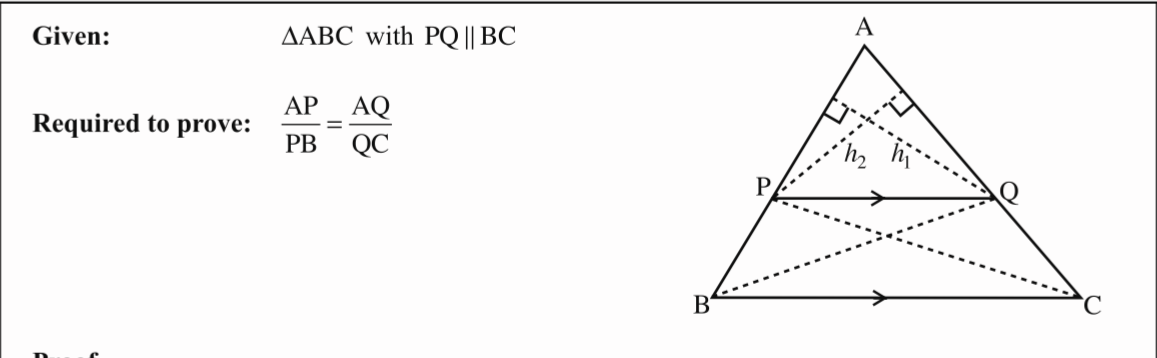
Proof of theorem 1:

Solution to proof:

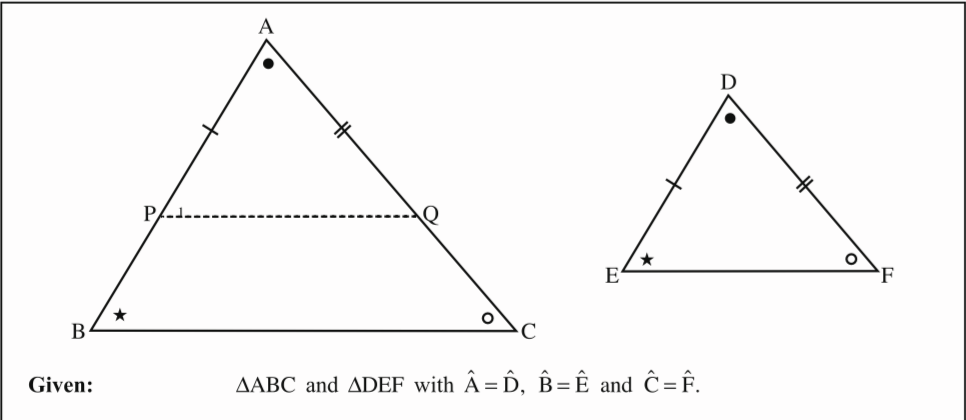
Proof of Theorem 2:

Proof:

Theorem 3 :

Proof: