Ch 1.1 Systems of Linear Equations

Vocabulary flashcards covering key terms from Section 1.1: Systems of Linear Equations.

System of Linear Equations

A collection of one or more linear equations involving the same variables x_1,\ldots,x_{n} .

Linear Equation

An equation that can be written as a_1x_1 + a_2x_2 + … + a_nx_n = b, where the coefficients a_1,\ldots,a_{n} and the constant b are real or complex numbers.

Solution

A tuple (x_1,…,x_n) of numbers that makes every equation in the system true when substituted.

Solution Set

The complete set of all solutions to a linear system.

Equivalent Systems

Two systems that have the same solution set.

Consistent

A system that has at least one solution (one or infinitely many).

Inconsistent

A system that has no solution.

No Solution

A situation where no assignment of values satisfies all equations in the system.

Exactly One Solution

A system that has a single, unique solution.

Infinitely Many Solutions

A system that has an infinite number of solutions.

Coefficient Matrix

The rectangular array containing only the coefficients of the variables from a linear system.

Augmented Matrix

The coefficient matrix with an added column containing the constants from the right-hand sides.

Matrix Size

The dimensions mxn of a matrix, read as 'm by n' (m rows, n columns).

Elementary Row Operations

The three operations used to simplify a system: replace a row by the sum of itself and a multiple of another row; interchange two rows; and multiply a row by a nonzero constant.

Row Equivalence

Two matrices are row equivalent if one can be transformed into the other by a sequence of elementary row operations; they have the same solution set for their associated systems.

Triangular Form

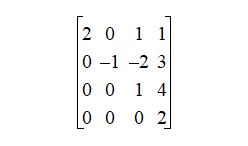
A form of the augmented matrix (or the system) where equations are arranged so that the leading (first nonzero) entry moves to the right as you go down, enabling step-by-step solving.

Existence and Uniqueness Questions

Two questions used to classify a linear system: (1) Is the system consistent? (2) If consistent, is the solution unique?

Check Solution

Substituting the found solution back into the original equations to verify correctness.

Floating Point Arithmetic

Real-number arithmetic on computers with finite precision, which can introduce rounding errors; software often uses floating point representations.