Lecture 1 - Vectors and Kinematics

What is a scalar

A SINGLE number (with a unit) that describes PHYSICAL QUANTITY

What is a vector

A quantity with both SIZE and DIRECTION

Magnitude of a vector is drawn like WHAT

| A (with arrow on top) | or A

Vectors are equal if they have the same WHAT and WHAT

Vectors are equal if they have the same MAGNITUDE (size) and DIRECTION

If your subtracting vectors how do you do it

Flip the direction

If your multiplying vectors how do you do it

Break it down to the addition and add like normal tip to tail

Any vector can be represented as a sum of two WHAT

Perpendicular vectors (Px and Py)

^I is WHAT

Is a dimensional vector length of 1 that points in the POSITIVE x DIRECTION

^J is WHAT

Is a dimensional vector length of 1 that points in the POSITIVE y DIRECTION

^K is WHAT

Is a dimensional vector length of 1 that points in the POSITIVE z DIRECTION (3D)

What is direction

Given by the angle COUNTER clock-wise from the x-axis

Taking the ratio Ay/Ax gives tangent of an WHAT between the WHAT and the WHAT

Taking the ratio Ay/Ax gives tangent of an ANGLE between the HORIZONTAL DIRECTION and the VECTOR

R = A + B (how do you add them)

R = (A + B) x + (A+B) y

What are the equations for the scalar (dot) product of two vectors ( A dot B )

A dot B = A x B x Cos(θ)

or

A dot B = AxBx + AyBy + AzBz

or

A dot B = AxBx + AyBy

if θ = 90 the product is WHAT (dot)

Zero

if θ < 90 the product is WHAT (dot)

positive

if θ > 90 the product is WHAT (dot)

Negative

if θ = 180 the product is WHAT (dot)

Negative

if θ = 0 the product is WHAT (dot)

Positive

What are the equations for the scalar (cross) product of two vectors ( A x B )

A x B = A x B x Sin(θ)

or

A x B = (AxBy - AyBx) K

A x B = A x B x Sin(θ) direction is given by the WHAT

Right hand rule

Right hand rule = Point the fingers of your right hand along the WHAT vector in the cross product (WHAT), then curl them so they point to the WHAT vector (WHAT). Your thumb gives the direction of the WHAT

Right hand rule = Point the fingers of your right hand along the FIRST vector in the cross product (Vector A), then curl them so they point to the SECOND vector (Vector B). Your thumb gives the direction of the CROSS PRODUCT

Out of page = WHAT

Positive

Into page = WHAT

negative

if θ = 180 the product is WHAT (cross)

zero

if θ = 90 the product is WHAT (cross)

zero

if θ < 90 the product is WHAT (cross)

A x B < AB

if θ = 90 the product is WHAT (cross)

A x B = AB

if θ > 90 the product is WHAT (cross)

A x B < AB

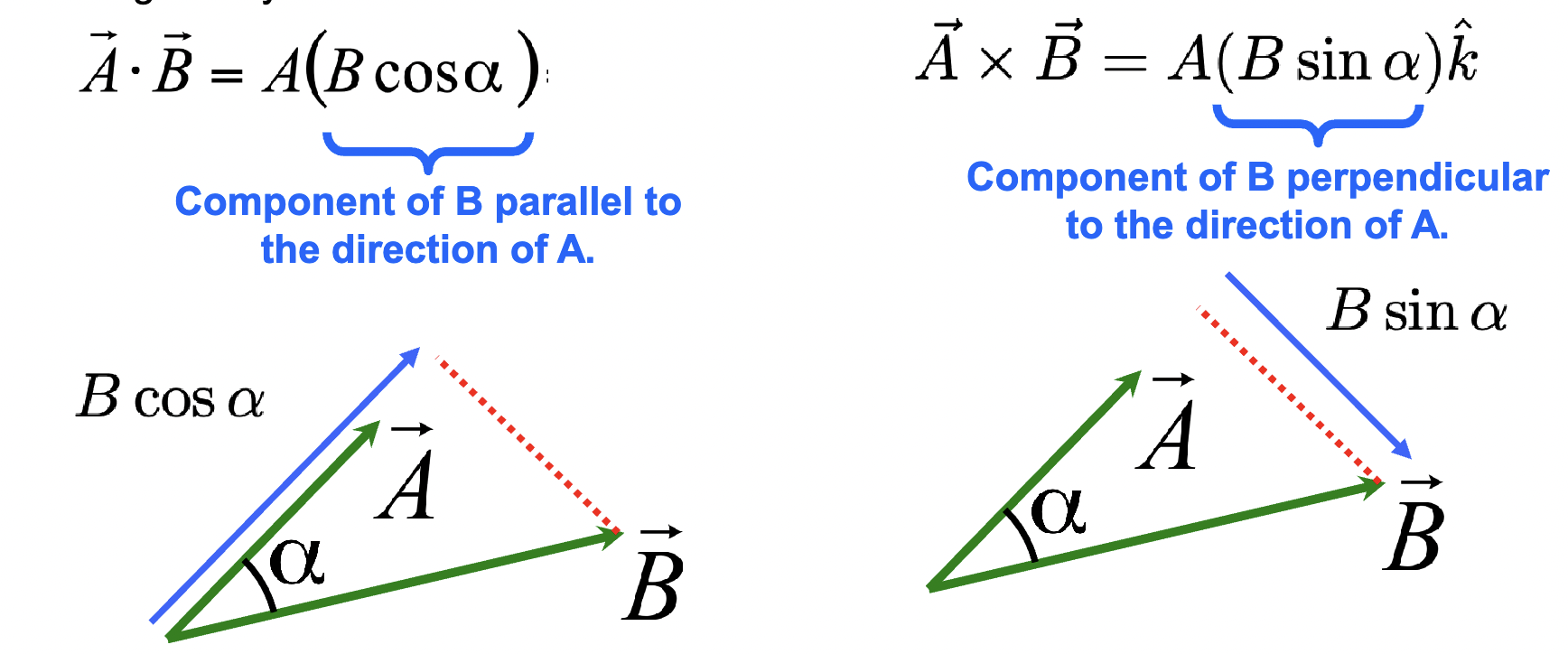
Dot vs cross product:

• A (dot) B = A(B cos(a)) = component of B is WHAT to the direction of A

• A x B = A (B sin(a)) = Component of B WHAT to the direction of A

Dot vs cross product:

• A (dot) B = A(B cos(a)) = component of B is PARALLEL to the direction of A

• A x B = A (B sin(a)) = Component of B PERPENDICULAR to the direction of A

Motion diagrams show representation/image of an object at WHAT

Fixed time intervals

If an object is speeding up the distance gets WHAT

Larger

If an object is SLOWING DOWN the distance gets WHAT

Smaller

If an object is at constant motion the distance is WHAT

The same

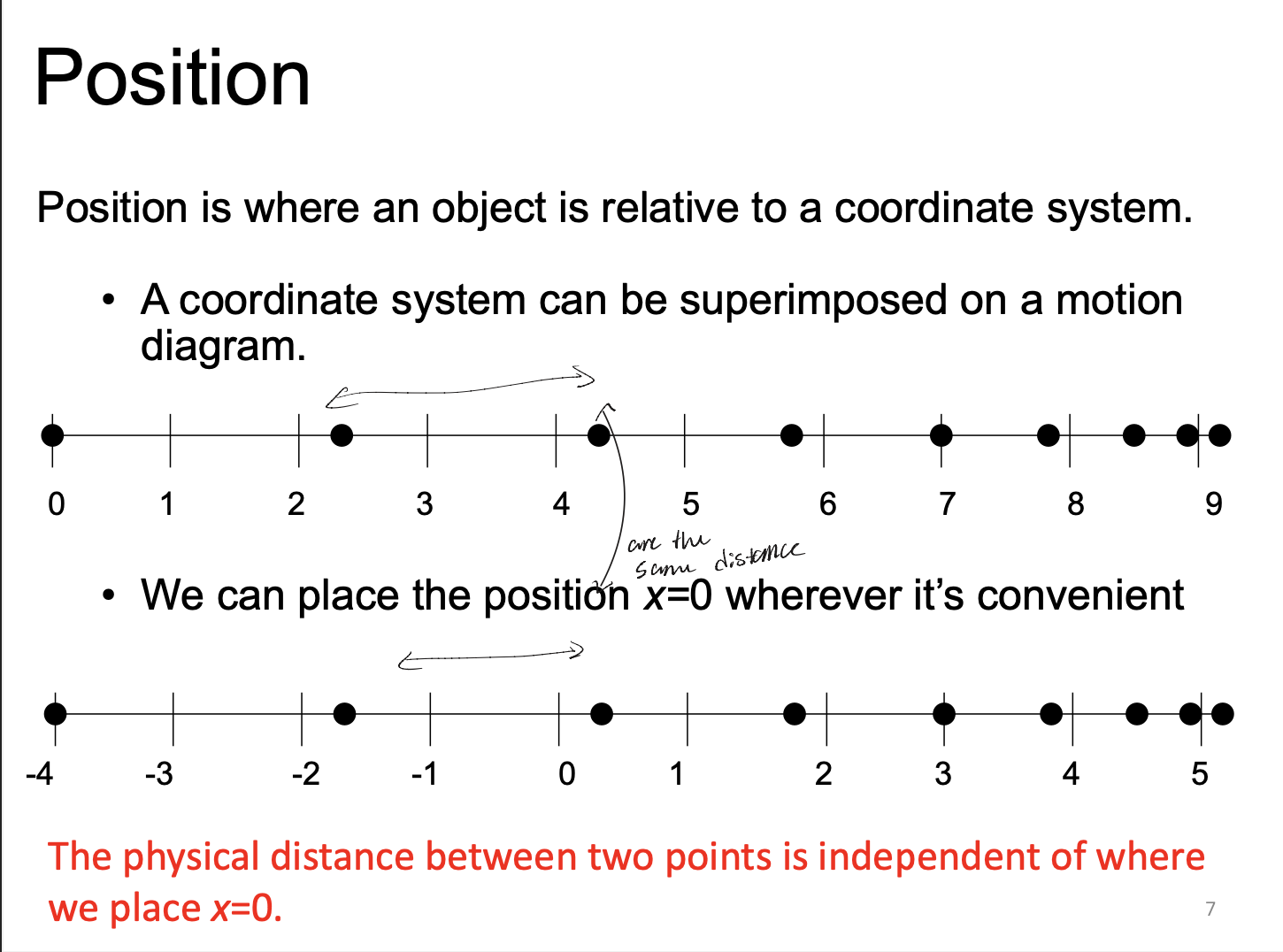
What is position

Position is where an object is relative to a COORDINATE SYSTEM

A coordinate system can be placed on a WHAT diagram

motion

We can place the position X = WHAT wherever

X = 0

The physical WHAT between two points is independent of where we place WHAT

The physical DISTANCE between two points is independent of where we place X = 0

What is mechanism

The study of the MOTION of objects and related concepts of FORCE and ENERGY

What is kinematics

Describes HOW objects move

What is dynamics

Describes WHY objects move

A position vector always extends from the WHAT to the WHAT

A position vector always extends from the ORIGIN to the LOCATION

Displacement is the WHAT

Change in position (final minus initial)

Δr = rf - ri

Position:

• Defines the WHAT of on object

• Represented by WHAT

• Is a VCTOR pointing from the WHAT to the WHAT

Position:

• Defines the LOCATION of on object

• Represented by r

• Is a VECTOR pointing from the ORIGIN to the OBJECT

Displacement:

• Separation between two WHAT

• Represented by WHAT

• Is a VECTOR pointing from WHAT to the WHAT

Displacement:

• Separation between two POSITION VECTORS

• Represented by Δr = rf - ri

• Is a VECTOR pointing from START to the FINISH

Distance:

• The WHAT path-length traversed by the object

• Represented by WHAT

• Is a WHAT

Distance:

• The TOTAL path-length traversed by the object

• Represented by d

• Is a SCALAR

Speed is “how WHAT” an object is moving

Speed is “how FAST” an object is moving

Velocity is “how WHAT and in what WHAT” is an object moving

Velocity is “how FAST and in what DIRECTION” is an object moving

What is teh equation for speed

speed = distance/ Δt

What is the equation for velocity

v = displacement / Δt

Therefor speed is a WHAT and velocity is a WHAT

Therefor speed is a SCALAR and velocity is a VECTOR

What is the equation for acceleration

Vavg = Δr/Δt = displacement/ Δt

Velocity always points in the same direction as WHAT

Δr

Any change in an objects VELOCITY is called an WHAT

Acceleration

If a runners speed is increasing acceleration = WHAT and points where

a doesnt = 0 →

If a car is slowing down acceleration = WHAT and points where

a doesnt = 0 ←

Direction depends on the direction of the WHAT relative to the direction of the WHAT

Direction depends on the direction of the VELOCITY relative to the direction of the ACCELERATION

if → +V

than

→ +a (WHAT)

← -a (WHAT)

if → +V

than

→ +a (speeding up)

← -a (slowing down)

if ← -V

than

→ +a (WHAT)

← -a (WHAT)

if ← -V

than

→ +a (Slowing down)

← -a (speeding up)