The Collective Honors physics knowt

Instantaneous velocity

average velocity over infinitesimally small time interval

Tangent line

straight line connecting a pair of infinitely close points on a curve

Time derivative

rate of value a function changes over time

acceleration

vector that is a derivative of velocity (m/s²)

constant accelerated motion

motion w/ constant acceleration

Instantaneous acceleration

average acceleration over infinitesimally small interval

Equations of motion

equations that describe an object’s displacement and velocity when acceleration is constant

v = v_i + at

Equation of motion (velocity)

C, B, D, F, G, A, E

Unscramble these terms in order of their derivatives:

A: crackle

B: velocity

C: position

D: acceleration

E: pop

F: jerk

G: snap

a = delta v/ delta t

acceleration equation

v= at + v_i

velocity vs. time slope intercept formula

negative velocity

if one were to take the tangent of a point on the descending part of the curve on this position vs. time graph, what would be the velocity

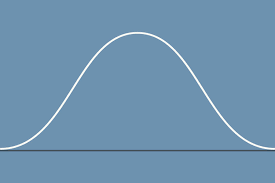
0 velocity

if one were to take the tangent of a point on the peak part of the curve on this position vs. time graph, what would be the velocity

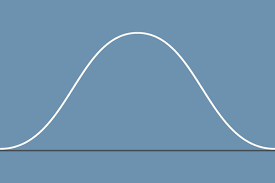
positive velocity

if one were to take the tangent of a point on the acsending part of the curve on this position vs. time graph, what would be the velocity?

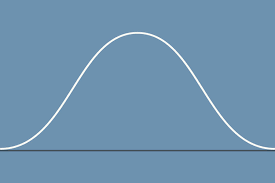
negative acceleration

if one were to take the tangent of a point on the descending part of the curve on this velocity vs. time graph, what would be the acceleration?

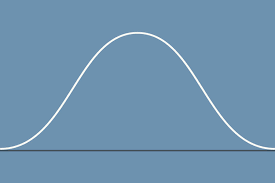
0 acceleration

if one were to take the tangent of a point on the peak part of the curve on this velocity vs. time graph, what would be the acceleration?

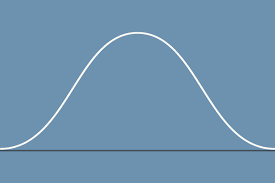
acceleration is positve

if one were to take the tangent of a point on the acsending part of the curve on this velocity vs. time graph, what would be the acceleration?

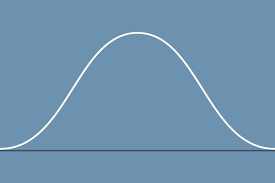
acceleration

the slope for a velocity vs.time graph is

object faced down

if one were to take the tangent of a point on the descending part of the curve on this acceleration vs. time graph, what would be the jerk?

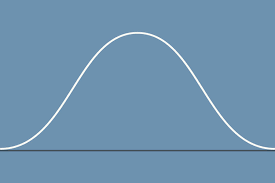
no jerk

if one were to take the tangent of a point on the peak part of the curve on this acceleration vs. time graph, what would be the jerk?

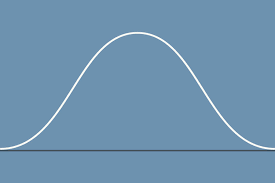
Object faced up

if one were to take the tangent of a point on the ascending part of the curve on this acceleration vs. time graph, what would be the jerk?

position

a measurement of where an object is at a particular time in respect to a reference point

Displacement

object’s change of position

Distance traveled

total length of path between two positions

change in d = d_f - d_i

displacement equation

scalar quantity

quantity with now direction but magnitude/size

vector quantity

quantity having both magnitude and direction

d = (x)x^ + (y)y^

components

IdI = sqrt((x)²+(y)²)

displacement

Resultant

vector that is a sum of two or more vectors

motion diagram

displays object’s position at equal increments in time

Dot diagram

motion diagram where object is represented by a dot

uniform motion

straight line motion when change interval is equal

nonuniform motion

position dose not change the same amount

position graph

position as a function of time

velocity

a measure of amount of change in position at specified time

speed

measurement of distance traveled in amount of time

v = delta d/delta t

velocity slope equation

d = vt +d_i

slope intercept form for position vs. time graph

displacement

area under velocity vs. time graph

negative

If an object is returning to it’s original position, the velocity will be ____

equal, opposite

If two non-zero vectors are added together, and the resultant vector is zero, what must be true of the two vectors?

they have ___ magnitude and ___ direction

integral

the area under a curve under a graph

delta d= v_it+1/2at²

equation of motion for displacement

free fall

the falling motion of an object without resistance under the influence of Earth’s gravity

acceleration due to gravity

the constant acceleration towards the center of Earth experienced by a body in free fall near Earth’s surface

delta y= v_it+1/2gt²

equations of motion for free fall (product is displacement in the y-direction)

v=v_i+gt

Equations of motion free fall (product is velocity)

v=(x)x^+(y)y^

velocity in components

sqrt((x)²+(y)²)

velocity’s magnitude

independent

horizontal and vertical components are _________ of each other

x, y

when adding two velocities, it is like displacement. Add_______ to x and ______ to y to make components for resultant vector

Pythagorean theorem

when you add two resultant vectors, what equation will you use?

projectile

object moving through air that is only affected by gravity

projectile motion

combo of uniform motion parallel to earth’s surface and free-fall motion perpendicular to earth’s surface

separating

projectile motion is analyzed by ______ the two-dimensions into separate dimensions

uniform, does not

horizontal motion is _______ and velocity __________ change

free-fall, increases

vertical motion is ___________ and __________ if going down

t

accelerated motion that is a parabola will have a _____ x-axis

x

trajectory graph will have a _____ on the x axis

y(x)=ax²+bx+c

parabola problem

trajectory graph

2 dimensional dot plot that displays total trajectory

delta x= v_xt

horizontal equation of motion

v_y=v_iy+gt

Velocity equation of motion with answer as vertical velocity component

delta y = v_iyt + ½gt²

Velocity equation of motion with vertical displacement component as the answer

x

trajectory is a quadratic function of __

t

Change in y position is a quadratic function of __

delta x, v_x, t

X motion variables

delta y, g, t, v_y, v_iy

y motion variables

v_iy=0

If an object is launched horizontally off a table, then _____

0

If launched upwards, and object’s y velocity at maximum ______

constant

v_x is ______

v_y

v_iy and v_y are the same absolute value, but ___ is negative

uniform circular motion

The motion observed when an object travels in a circular path at constant speed

constant, changes

in uniform circular motion, the magnitude of velocity is _____, and velocity _______

Centripetal vector

A vector quantity that is always directed towards the center of the circle

centripetal acceleration

acceleration of an object in uniform circular motion

a_c = v²/R

centripetal acceleration equation

oscillatory motion

any motion in which an object repeats the same pattern of motion while repeatedly returning to the same position

x=Rcos((v/R)t)

oscillatory motion x equation

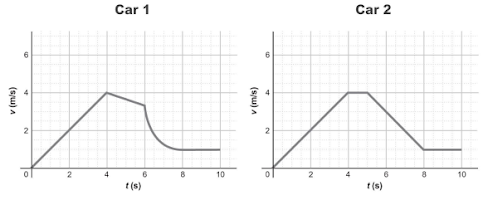
The area is greater under car 2’s graph

Car 2 has a larger displacement. How would you find this out?

y= Rsin((v/R)t)

oscillary motion y equation

It would take longer because no outside velocity besides free fall is affecting them and deceleration is directly related to the speed.

If a student throws up a ball with twice it’s initial speed, how would the air time change?

the point, after

When a problem asks for the instantaneous value from a graph, you should take the _____ and the point _____ it

There is gravitational acceleration to speed it up

Why do objects fall faster on earth than in a vaccuum?

Split it into a triangle and rectangle and add the two values together

if you’re looking for the displacement under a graph and you encounter a irregular shape, you should ____

ΣF=ma

Newton’s seconds law of motion (force)

Newton’s first law of motion

a law that states that an object remains at rest or continue with uniform motion in a straight line unless some action causes a change in motion

ΣF= delta p/ delta t

Newton’s Seconds Law of motion with momentum

p= mv

Momentum equation

Inertia

object’s resistance to change

Mass

measure of object’s inertia (measured in the SI unit of kg)

Force

The cause of a change in motion or change in shape resulting from the unopposed interaction between two objects

net force

vector sum of all net forces

momentum

product of mass and velocity of an object; represents object’s total quantity of motion

Newton’s third law of motion

interaction between two objects can be represented as forces having equal magnitude and opposite directions

Third Law pair

the two related action-related forces described by newton’s third law

Contact Force

an interaction between objects due to direct contact with each other

noncontact force (field force)

interaction between two objects that are separated by some distance

gravitational force (gravity)

the noncontact attractive interaction between tow objects having mass