ANALIZIS 2 DEF

OE-NIK

Valódi tör

Ha a törtfüggvény számlálója alacsonyabbfokú mint a nevezője.

Függvénygörbe alatti terület

Az [a, b] intervallumon értelmezett, nemnegatív, folytonos f függvény grafikonja alatti terület, azaz az y = f (x) egyenletu görbe, az ̋ x = a, x = b egyenesek és az abszcisszatengely által határolt tartomány területe alatt az f függvény [a, b] intervallumon vett határozott integrálját értjük.

Függvénygörbe feletti terület

Ha a g függvény az [a, b] intervallumon értelmezett, folytonos és csak negatív értékeket vesz fel, akkor integrálja negatív, de integráljának abszolút értéke ekkor is a megfelelo síkidom területe.

Két függvénygörbe közé zárt terület

Ha f és g az [a, b] intervallumon értelmezett és ott integrálható valós-valós függvények, amelyekre ∀x ∈ [a, b] esetén f (x) ≤ g (x), akkor a függvénygörbék által meghatározott normáltartomány területe: 𝑇 = ∫^b_a(𝑔 − 𝑓)

Rektifikálható

Egy folytonos síkgörbét rektifikálhatónak nevezünk, ha a görbéhez írt poligonok hosszának szuprémuma véges. Ha a görbe rektifikálható, akkor ívhosszán éppen a fenti szuprémumot értjük.

Folytonosan differenciálható:

Az f függvényt folytonosan differenciálhatónak nevezzük az I intervallumon, ha f differenciálható ∀x ∈ I esetén és f deriváltfüggvénye folytonos I-n.

Improprius Integrál fajtái

Függvényegyenlet

Az olyan egyenleteket, amelyekben a meghatározandó ismeretlen függvény, függvényegyenletnek nevezzük.

Differenciálegyenlet

Az olyan függvényegyenletet, amelynek felírásában az ismeretlen függvény mellett annak (valahányadrendu) ̋ deriváltfüggvénye is szerepel differenciálegyenletnek nevezzük.

Függvényváltozó:

x

Függvény

y(x) -> y

Rend

A differenciálegyenlet rendje az ismeretlen függvény deriváltjai rendjének maximuma az egyenletben

Lineáris

A differenciálegyenlet lineáris, ha benne az ismeretlen függvénynek és deriváltjainak csak elso hatványa szerepel, és nem ̋ fordul elo ezek szorzata sem.

Algebrai differenciálegyenlet

A differenciálegyenlet algebrai, ha benne az ismeretlen függvénynek és deriváltjainak csak polinomja szerepel.

Transzcendens

A differenciálegyenlet transzcendens, ha nem algebrai

Közönséges differenciálegyenlet

Közönséges differenciálegyenletnek nevezzük az olyan differenciálegyenletet, amelyben az ismeretlen függvény egyváltozós

Parciális differenciálegyenlet

Parciális differenciálegyenletnek nevezzük az olyan differenciálegyenletet, amelyben az ismeretlen függvény többváltozós.

Integrálgörbe

A differenciálegyenlet egy partikuláris megoldását ábrázolhatjuk a szokásos derékszögu koordinátarendszerben. Az így kapott grafikont szokás integrálgörbének nevezni.

Elsőrendű differenciálegyenlet

Elsőrendű lineáris differenciálegyenletnek nevezzük az olyan differenciálegyenletet, amely elsorendű és elsőfokú is.

Állandó együtthatósnak nevezzük

Ha az elsőrendű lineáris differenciálegyenlet általános alakjában a g függvény konstans, akkor állandó együtthatósnak nevezzük.

Állandó variálás módszere

A differenciálegyenlethez rendelt homogén egyenlet általános megoldásában a paraméter helyébe egy ismeretlen k (x) függvényt írunk. Az így kapott függvényt és deriváltját behelyettesítve a differenciálegyenletbe meghatározzuk az ismeretlen függvényt. A (mostmár ismert) k (x) függvényt a homogén egyenlet általános megoldásában a paraméter helyébe írva megkapjuk a differenciálegyenlet egy partikuláris megoldását.

Homogén-inhomogén

Ha az elsorendű lineáris differenciálegyenletben a h függvény (az ún. zavaró függvény) azonosan 0, akkor a differenciálegyenlet homogén, ellenkezo esetben inhomogén

Próba függvény módszer

Abban az esetben, ha a lineáris differenciálegyenlet állandó együtthatós, akkor használhatjuk az ún. Próbafüggvénymódszert. Ez azt jelenti, hogy a partikuláris megoldást olyan alakban keressük, ami „hasonló" a zavaró függvényhez.

Hiányos differenciálegyenletek:

Ha a másodrendű differenciálegyenletben az ̋ x változó az y függvény és annak yʹ deriváltfüggvénye közül valamelyik (esetleg közülük több) nem szerepel, akkor hiányos másodrendu differenciálegyenletr ̋ -ől ̋ beszélünk.

Lineárisan független - Lineárisan összefüggő

Az I intervallumon értelmezett y1 és y2 függvényeket lineárisan függetleneknek nevezzük, ha a c1y1 + c2y2 = 0 (c1, c2 ∈ R) azonosság csak akkor teljesül, ha c1 = c2 = 0. Ha két függvény nem lineárisan független, akkor lineárisan összefüggok ̋ a kérdéses intervallumon.

Karakterisztikus egyenlet

Az ayʹʹ + byʹ + cy = 0 másodrendu, lineáris, állandó együtthatós, homogén differenciálegyenlet karakterisztikus egyenletén az aλ2 + bλ + c = 0 másodfokú egyenletet értjük.

Rezonancia

Ha a differenciálegyenlethez rendelt homogén egyenlet megoldásában van olyan tag, amely nem lineárisan független a felírt próbafüggvény valamely tagjától (hányadosuk állandó), akkor rezonancia esete áll fenn. Ilyenkor a próbafüggvényben a lineárisan függo tagot x-szel megszorozzuk.

Laplace-integrál

A Laplace-transzformált definíciójában szereplő integrált Laplace-integrálnak nevezzük. f függvény Laplace-transzformáltja: 𝐹 (s)= 0->∞ INT f(t)*e^-st

Laplace-integrál konvergenciája

A Laplace-integrál vagy minden valós számra konvergens, vagy egy valós számra sem konvergens, vagy létezik olyan a ∈ R szám, hogy minden Re s > a számra az integrál konvergens, de minden Re s < a számra az integrál divergens.

A Laplace-integrál konvergenciájának elégséges feltétele

Ha létezik olyan 𝛼 ∈ R, 𝑘 ∈ R+ és 𝑡 ∈ R+ szám, hogy t > t0 esetén |𝑓(t)| ≤ 𝑘 ⋅ e^at , akkor Re s > α esetén az f függvény Laplace-integrálja abszolút konvergens.

A Laplace-transzformáció homogén, lineáris

L[f1(t) + f2(t)] = L[f1(t)] + L[f2(t)] L[c · f(t)] = c · L[f(t)]

Inverz Laplace-transzformáció

Ha az f (t) függvény laplace-transzformáltja F (s), akkor f (t)-t az F (s) függvény inverz Laplace-transzformáltjának nevezzük.

Függvénysorozat

Függvénysorozatnak nevezzük az olyan pozitív egész számok halmazán értelmezett függvényt, ami minden pozitív egész számhoz hozzárendel egy

függvényt: 𝑛 ↦ 𝑓

Függvénysorozat értelmezési tartománya

A függvénysorozat értelmezési tartományán a sorozatban szereplo egyes függvények értelmezési tartományainak metszetét ér

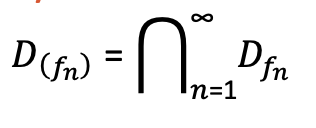
tjük:

Függvénysorozat konvergenciatartománya

Az (𝑓_n ) függvénysorozat konvergenciatartományán azt a halmazt értjük, amely (𝑓_n ) értelmezési tartományyának pontosan azokból a pontjaiból áll, amelyekben a függvénysorozat konvergens.

Függvénysorozat határfüggvénye

Az (𝑓_n ) függvénysorozat határfüggvényén azt az f függvényt értjük, amelynek értelmezési tartománya megegyezik (f_n) konvergenciatartományával és amelyre 𝑓(x) = lim_n→ +∞ 𝑓_n (𝑥) a függvénysorozat konvergenciatartományának minden x pontjában.

Függvénysorozat egyenletesen konvergens

Az (fn) függvénysorozat egyenletesen konvergens az I intervallumon, ha minden 𝜖 > 0 számhoz megadható olyan n𝜖 ∈ Z+ küszöbindex, amelyre teljesül hogy n>n𝜖 esetén az I intervallum bármely x helyén | fn(x) - f(x) | < 𝜖.

Függvénysor:

Legyen az f1, f2, . . . , fn . . . függvények értelmezési tartományainak közös része nem üres. Ekkor a ∑^∞_k=1 𝑓_k formális összeget függvénysornak nevezzük.

Függvénysor tagjai

Az f1, f2, . . . , fn . . . függvényeket a függvénysor tagjainak nevezzük.

Függvénysor n-edik részletösszege

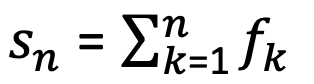
Függvénysor n-edik maradékösszegének

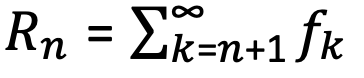
Függvénysor értelmezési tartománya

Függvénysor értelmezési tartományán a tagjai értelmezési tartományának metszetét értjük.

Függvénysor konvergens X0 pontban

Függvénysor konvergencia-tartománya

Az a halmaz, amely az értelmezési tartományának azon pontjaiból áll, amelyekben a függvénysor konvergens.

Függvénysor egyenletesen konvergens

függvénysor egyenletesen konvergens az I intervallumon, ha bármely 𝜖 > 0 számhoz található olyan n𝜖 ∈ Z+ küszöbindex, amelyre teljesül hogy n>n𝜖 esetén | sn(x) - s(x) | < 𝜖.

Függvénysor abszolút konvergens

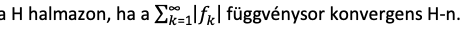
Függvénysor egyenletesen konvergens

Ha a ∑∞ 𝑓 függvénysor egyenletesen konvergens az I intervallumon és tagjai folytonosak ezen az intervallumon, akkor a függvénysor S összegfüggvénye is folytonos I-n.

Függvénysor differenciálhatósága

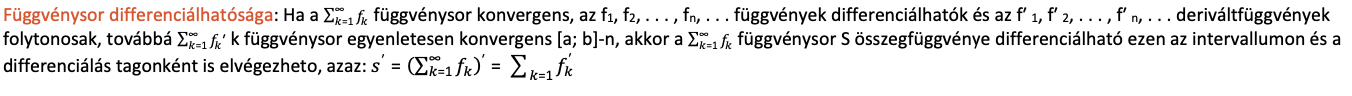
Hatványsor

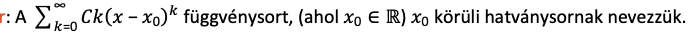
Abel-tétel

Konvergenciasugár

Az r számot konvergenciasugárnak nevezzük. Ha a hatványsor konvergencia-tartománya R, akkor r = ∞.

Abszolút és egyenletesen konvergens

Ha egy hatványsor konvergenciasugara r > 0, akkor ez a hatványsor abszolút és egyenletesen konvergens minden [a; b] ⊆] − r; r[ zárt intervallumon.

Taylor - sor

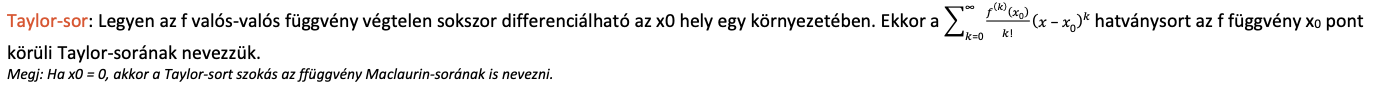
Taylor polinom

Taylor - formula

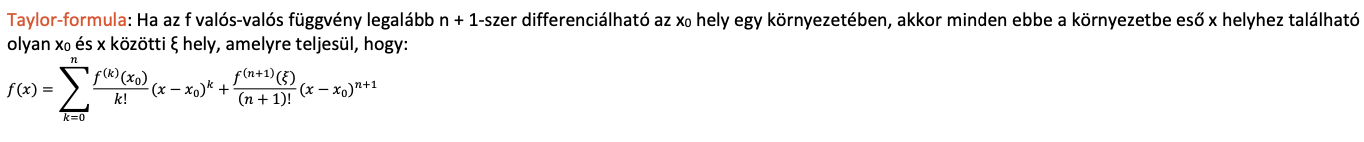
Lagrange féle maradéktag

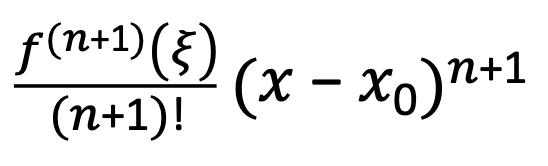
Taylor-sor maradéktag

Ha az f valós-valós függvény az x0 hely egy környezetében végtelen sokszor differenciálható, és ezen környezet minden x pontjában a az x0-körüli Taylor-formula Lagrange-féle maradéktagja a 0-hoz tart n → ∞ esetén, akkor f Taylor-sora konvergens ebben a környezetben és eloállítja az f függvényt.

Páros és páratlan függvények Maclaurin-sora

: Ha az f valós-valós függvény páros és sorba fejthető a 0 körül, akkor Maclaurin sora csak páros (vagy csak páratlan) kitevőjű tagokat tartalmaz