Geometry Quarterly #2
5.0(1)
5.0(1)
Card Sorting
1/97
Earn XP
Description and Tags
Study Analytics
Name | Mastery | Learn | Test | Matching | Spaced |
|---|
No study sessions yet.
98 Terms
1
New cards
complementary
2 angles that add up to 90 degrees, don’t have to be adjacent
2
New cards
supplementary
2 angles that add up to 180 degrees, don’t have to be adjacent
3
New cards
Linear pair
adjacent supplementary angles
4
New cards
vertical angles
when 2 lines intersect, the non-adjacent angles are vertical angles
5
New cards
vertical angles theorem
all vertical angles are congruent
6
New cards
transversal
a line that intersects two coplanar lines at two different points
7
New cards
corresponding angles
lie on the same side of the transversal and same sides of the intersecting lines
8
New cards
same-side interior angles
lie on the same side of the transversal and between the intersected lines
9
New cards
alternate exterior angles
lie on opposite sides of the transversal and outside the intersected lines
10
New cards
alternate interior angles
are nonadjacent angles that lie on opposite sides of the transversal between the intersected lines
11
New cards
parallel lines
lie in the same plane and never intersect →- indicates parallel lines same direction. ll symbolizes parallel too.
12
New cards
same-side interior angles postulate
if two parallel lines are cut by a transversal, then the pairs of same-side interior angles are supplementary
13
New cards
alternate interior angles theorem
if two parallel lines are cut by a transversal, then the pairs of alternate interior angles have the same measure
14
New cards
corresponding angles theorem
if two parallel lines are cut by a transversal, then the pairs of corresponding angles have the same measure
15
New cards
alternate exterior angles are…
congruent
16
New cards
transitive property
if a=b and b=c then a=c
17
New cards
subtraction property
an equal value subtracted or removed from two equal items will result in a new equal amount
if a=b then a-c=b-c
if a=b then a-c=b-c
18
New cards
substitution
if a=b then b can replace a in any case
19
New cards
converse of the same-side interior angles postulate
if two lines are cut by a transversal so that pair of same-side interior angles are supplementary, then the lines are parallel
20
New cards
converse of the alternate interior angles theorem
if two lines are cut by a transversal so that any pair of alternate interior angles are congruent, they are parallel
21
New cards
converse of the corresponding angle theorem
if two lines are cut by a transversal so that any pair of corresponding angles are congruent, then the lines are parallel
22
New cards
the parallel postulate
through a point “P” not on the “L” there is exactly one line parallel to “L”
23
New cards
Perpendicular bisector theorem
if a point is on the perpendicular bisector of a segment, then it is equidistant from the endpoints of a segment
24
New cards
Perpendicular line slope relationship
opposite reciprocal
25
New cards
Converse of the Perpendicular Bisector Theorem
If a point is equidistant from the endpoints of a segment, then it lies on the perpendicular bisector of the segment
26
New cards
distance formula
d=√(x₂-x₁)² + (y₂-y₁)²
27
New cards
point-slope formula
y - y₁ = m ( x - x₁ )
28
New cards
midpoint formula
(x₁ + x₂ / 2) , (y₁ + y₂ / 2)
29
New cards
slope formula
rise/ run y₂-y₁ / x₂-x₁
30
New cards
slope intercept form
y = mx + b
31
New cards
parallel line slope relationship
same slope
32
New cards
CPCFC
corresponding parts of congruent figures are congruent
33
New cards
CPCTC
corresponding parts of triangles are congruent (biconditional)
34
New cards
Bioconditional
p if and only if q - statement can be written in that form
Two triangles are congruent if and only if corresponding pairs of angles are congruent
Two triangles are congruent if and only if corresponding pairs of angles are congruent
35
New cards
Contrapositive
“if p then q” “if not q, then not p”
contrapositive of true statement is true
ex. if corresponding pairs of sides or corresponding pairs of angles are not congruent, then the triangles are not congruent
contrapositive of true statement is true
ex. if corresponding pairs of sides or corresponding pairs of angles are not congruent, then the triangles are not congruent
36
New cards
ASA
angle, included side, angle
37
New cards
ASA Triangle Congruence Theorem
if two angles and the included side of one triangle are congruent to. two angles and the included side of another triangle, then the triangles are congruent
38
New cards
reflexive property
a=a
39
New cards
midpoint
of a line segment is the point that divides the segment into two segments that have the same length
40
New cards
right angles
all right angles are congruent; 90 degrees
41
New cards
bisector
goes through an angle (angle bisector), segment (segment bisector), line to form two equal parts, angles, etc
42
New cards
congruent supplements theorem
if two angles are supplements of the same angle (or congruent angles) then the two angles are congruent
43
New cards
congruent complements theorem
if two angles are complements of the same angle (or congruent angles), then the two angles are congruent
44
New cards
regular polygon
all angle measures are the same, all side lengths are the same (equiangular and equilateral)
45
New cards
SAS
side, included angle, side
46
New cards
SAS Triangle Congruence Theorem
if two sides and the included angle of one triangle are congruent to two sides and the included angle of another triangle, the the triangles are congruent
47
New cards
perpendicular bisector
perpendicular bisector of a line segment is a line perpendicular to the segment at the segments midpoint. Form right angles
48
New cards
SSS
side, side, side
49
New cards
SSS Triangle Congruence Theorem
if three sides of one triangle are congruent to three sides of another triangle, then the triangles are congruent
50
New cards
two triangle congruence that don’t work
AAA & SSA
51
New cards
AAS
angle, angle, side
52
New cards
AAS Triangle Congruence Theorem
if two angles and a non-included side of one triangle are congruent to the corresponding angles and non-included side of another triangle, then the triangles are congruent.
53
New cards
HL
hypotenuse, leg
54
New cards
HL Triangle Congruence Theorem
if the hypotenuse and a leg of a right triangle are congruent to the hypotenuse and leg of another right triangle, then the triangles are congruent
55
New cards
pythagorean theorem
a² + b² = c² (a bottom, b side, c hypotenuse)
56
New cards
Triangle Sum Theorem
the sum of the angle measures of a triangle is 180 degrees
57
New cards
Polygon Angle Sum Theorem
the sum of the measures of the interior angles of a convex polygon with “n” sides is n-2(180)
58
New cards
concave
in, dip in shape “M”
59
New cards
convex
out, up ;“O”;”G"
60
New cards
exterior angle (polygon)
an angle formed by one side of a polygon and the extension of an adjacent side. Exterior angles form linear pairs with the interior angles
61
New cards
remote interior angle
an interior angle that is not adjacent to the exterior angle
62
New cards
exterior angle theorem
the measure of an exterior angle of a triangle is equal to the sum of the measures of its remote interior angles
63
New cards
isosceles triangle (know parts)
a triangle with at least two congruent sides
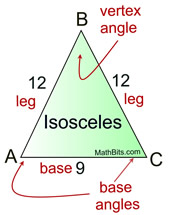
64
New cards
isosceles triangle theorem
if two sides of a triangle are congruent, then the two angles opposite the sides are congruent
65
New cards
Converse of the Isosceles Triangle Theorem
if two angles of a triangle are congruent, then the two sides opposite the angles are congruent
66
New cards
Equilateral Triangle
a triangle with 3 congruent sides
67
New cards
Equiangular Triangle
a triangle with 3 congruent angles
68
New cards
Equilateral triangle theorem
if a triangle is equilateral, then it is equiangular
69
New cards
Converse of the equilateral triangle congruence theorem
if a triangle is equiangular, then it is equilateral
70
New cards
Triangle Inequality Theorem
the sum of any two side lengths of a triangle is greater than the third-side length \*\***tip - add two smallest sides****
71
New cards
Side-Angle Relationships in Triangles
if two sides of a triangle are not congruent, then the larger angle is opposite the longer side (if AC>BC, then
72
New cards
Angle-Side Relationship in Triangles
if two angles of a triangle are not congruent, then the longer side is opposite the larger angle. (if BC)
73
New cards
A circle that contains all the vertices of a polygon is circumscribed about the polygon
circumcircle? circumcenter?
circumcircle? circumcenter?
circle is called circumcircle
the center of the circle is called the circumcenter
the center of the circle is called the circumcenter
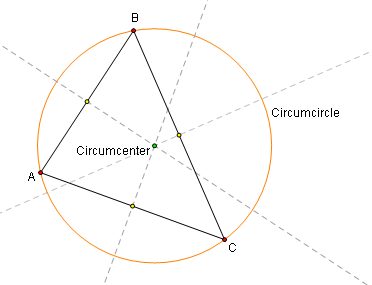
74
New cards
Point of Concurrency
Three or more lines are concurrent if they intersect at the same point. The point of intersection is called the point of concurrency.
75
New cards
Circumcenter Theorem
the perpendicular bisectors of the sides of a triangle intersect at a point that is equidistant from the vertices of the triangle PA=PB=PC
76
New cards
Acute Triangles (circumcenter location)
circumcenter is inside the triangle
77
New cards
Right Triangle (circumcenter location)
circumcenter is on the triangle
78
New cards
Obtuse Triangle (circumcenter location)
circumcenter is outside the triangle
79
New cards
the point from a point to a line is the…
length of the perpendicular segment from the point to the line
80
New cards
Angle Bisector Theorem
if a point is on the bisector of an angle, then it is equidistant from the sides of the angle
81
New cards
Converse of the Angle Bisector Theorem
if a point in the interior of an angle is equidistant from the sides of the angle, then it is on the bisector of the angle
AC = BC so…
AC = BC so…
82
New cards
When is a circle inscribed in a polygon? What’s an inscribed circle called?
if each side of the polygon is tangent (on) to the circle. The inscribed circle is called the incircle
83
New cards
The center of a circle inscribed in a triangle is called?
The *incenter* of the triangle
84
New cards
Incenter Theorem
the angle bisectors of a triangle intersect at a point that is equidistant from the sides of the triangle
85
New cards
Median
of a triangle is a segment whose endpoints are a vertex of a triangle and the midpoint
86
New cards
Centroid of a Triangle
the intersection (point of concurrency) of the three medians of a triangle
87
New cards
Where is the centroid regarding the triangle? What is it for a triangle?
inside the triangle; center of gravity of a triangle
88
New cards
Centroid Theorem
the centroid of a triangle is located 2/3 of the distance from each vertex to the midpoint of the opposite side
89
New cards
Altitude of a Triangle
perpendicular segment from a vertex to the line containing the opposite side; every triangle has 3 altitudes; not a bisector, doesn’t necessarily go to midpoint
90
New cards
Location of Altitude
can be inside, outside, or on the triangle
91
New cards
Orthocenter & Location?
the intersection (or point of concurrency) of the lines that contain the altitudes; can be inside, outside, or on the triangle
92
New cards
Acute Triangle (orthocenter triangle)
inside triangle
93
New cards
Right Triangle (orthocenter triangle)
on triangle
94
New cards
Obtuse Triangle (orthocenter triangle)
outside triangle
95
New cards
circumcenter
perpendicular bisectors
96
New cards
incenter
angle bisectors
97
New cards
centroid
medians
98
New cards
orthocenter
altitudes