binomial expansion

for non-natural numbers MOVE THIS DOWN

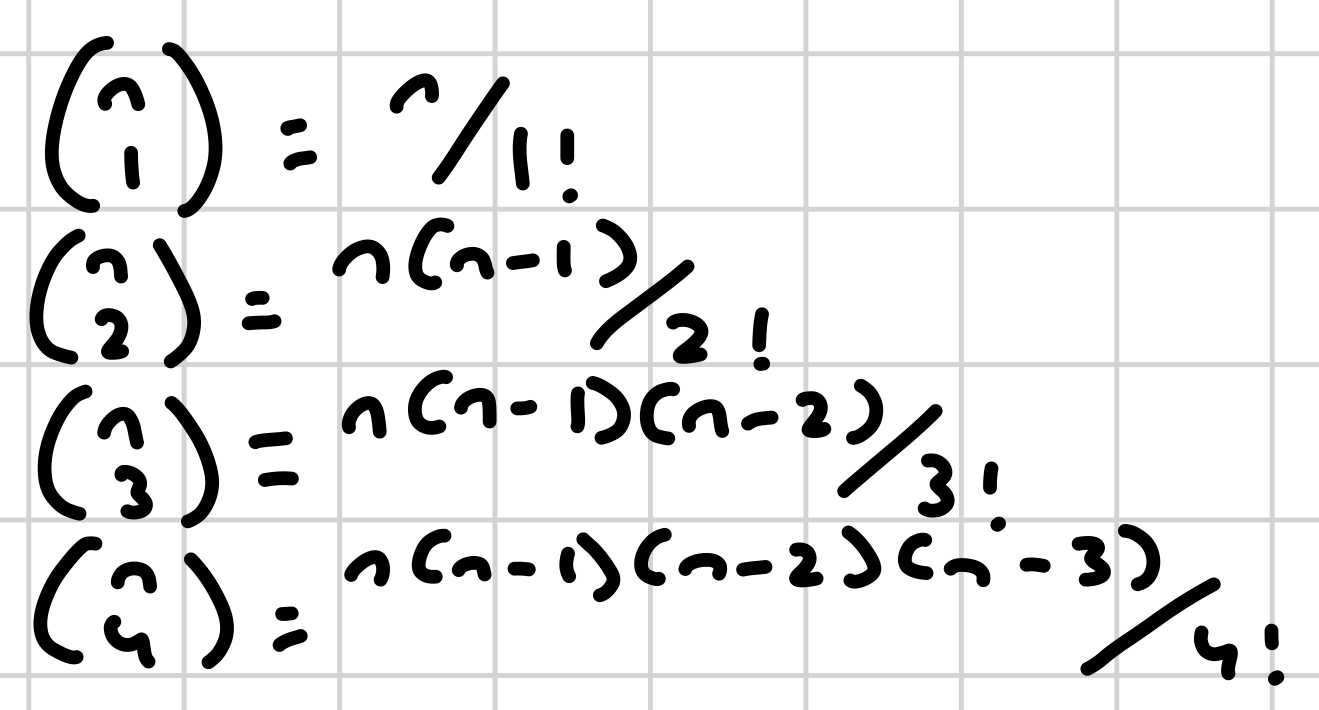
what does ! mean?

factorial

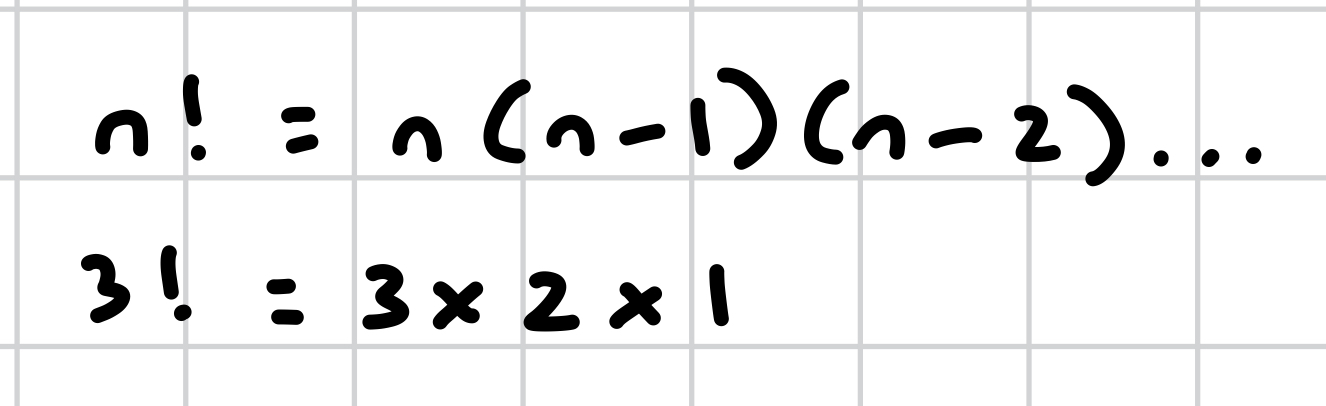
binomially expand (1 + x)^5

pascal’s triangle

which row do you start counting from on pascal’s triangle?

the second down, 1 1

what is significant about the binomial expansion of any term with a singular negative term?

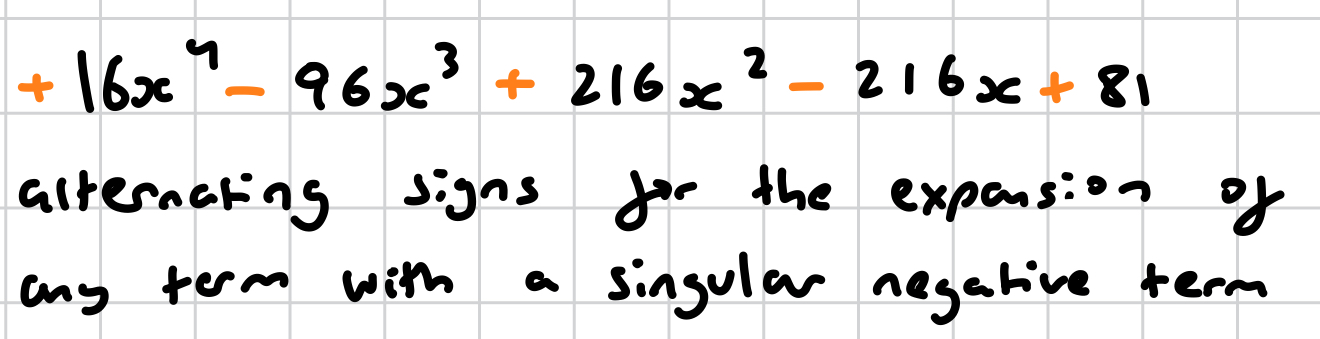
how do you solve this?

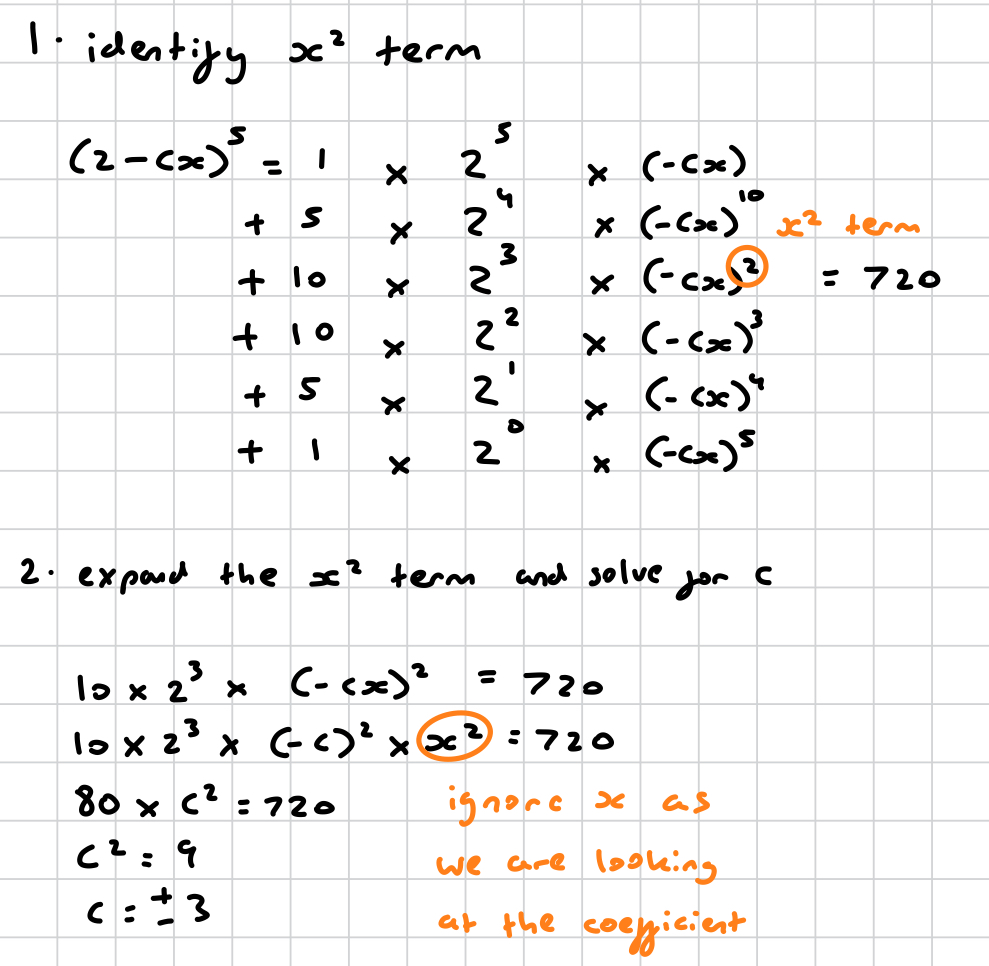
which terms have increasing powers and which have decreasing?

1st term - decreasing

2nd term - increasing

how do you find the nCr button on the calculator?

1. optn

2. F6 (>)

3. F3 (prob)

4. F3 (nCr)

how do you use the nCr button?

what does n factorial represent?

number of ways of arranging n objects in a line

what does ^ncr mean?

‘n choose r’ - the number of ways of choosing r items from a group of n items

how else is ncr written?

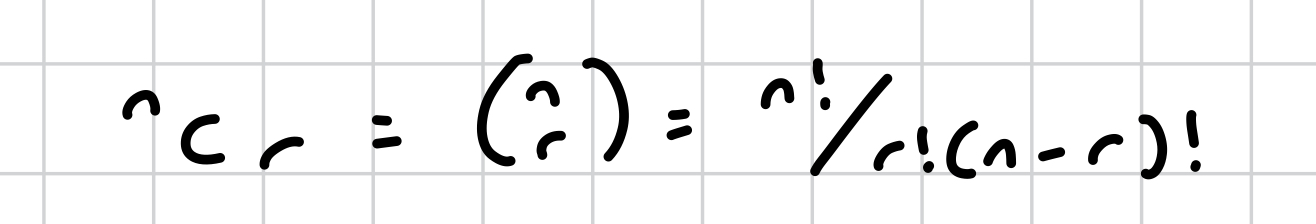
n = ?

row; i.e., power of x (x³ = 3rd row)

r = ?

position in row, starting with 0 for 1 because the first term is always 1 so it’s not typically calculated

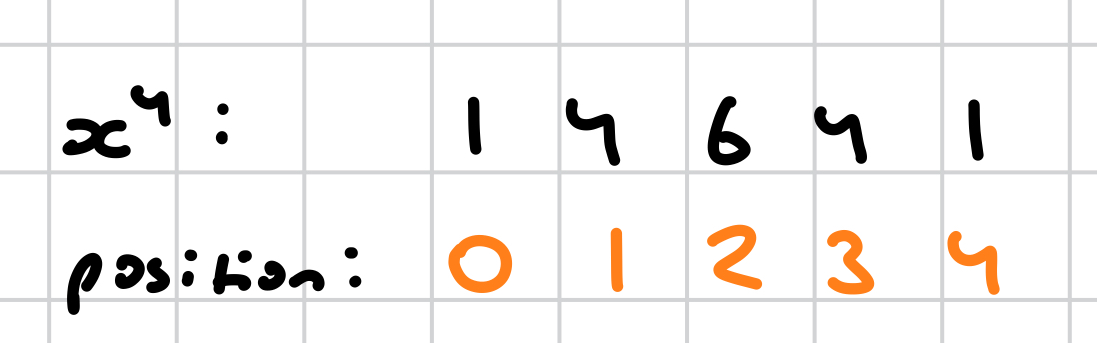
what is a binomial expression?

an expression that has 2 terms. e.g., in (x + 6), the 1st term is x and the 2nd is 6

what is the binomial expansion?

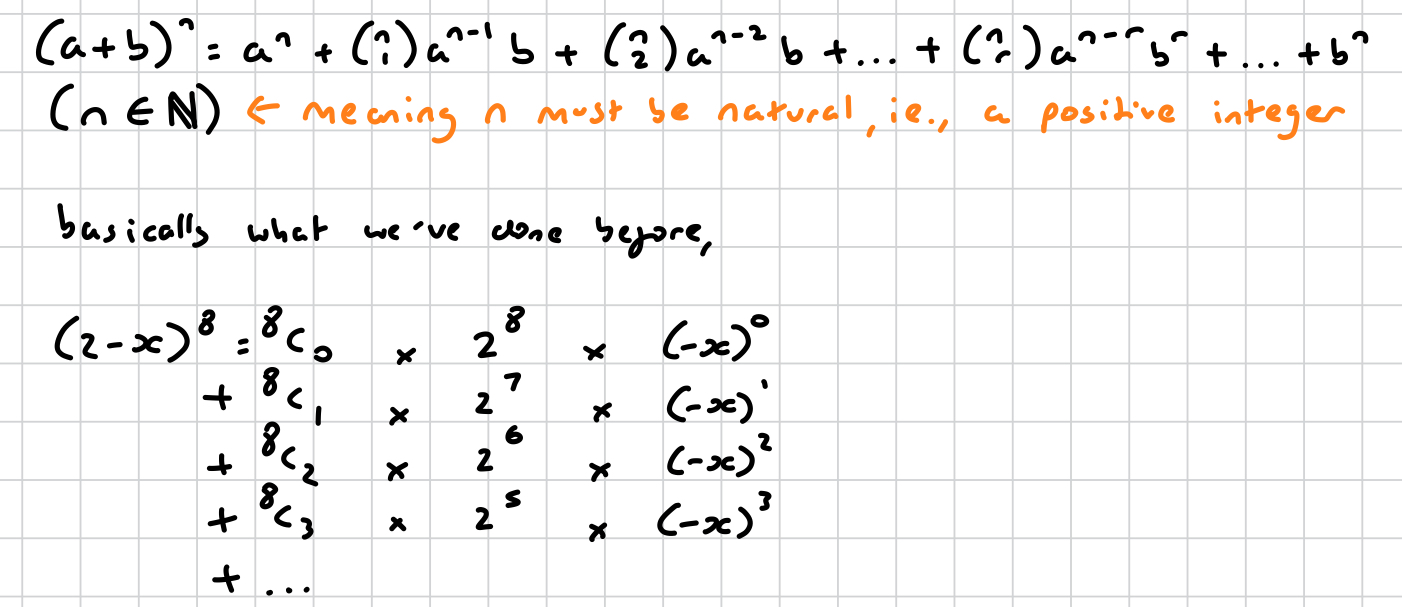
how many terms are there in a row?

+1 of the row number; e.g., x^5 has 6 terms as you need to account for x^0

what is the binomial expansion for individual coefficients?

should x be the a or b term?

b, always

how do you solve this?

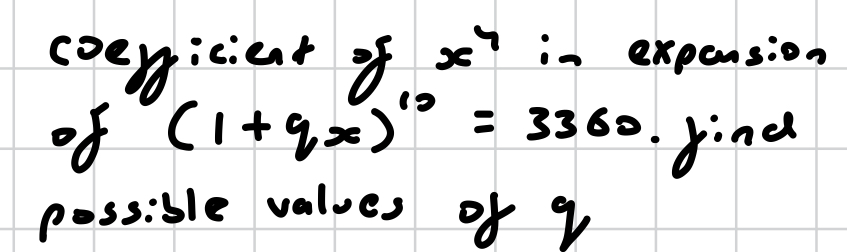
how do you solve this?

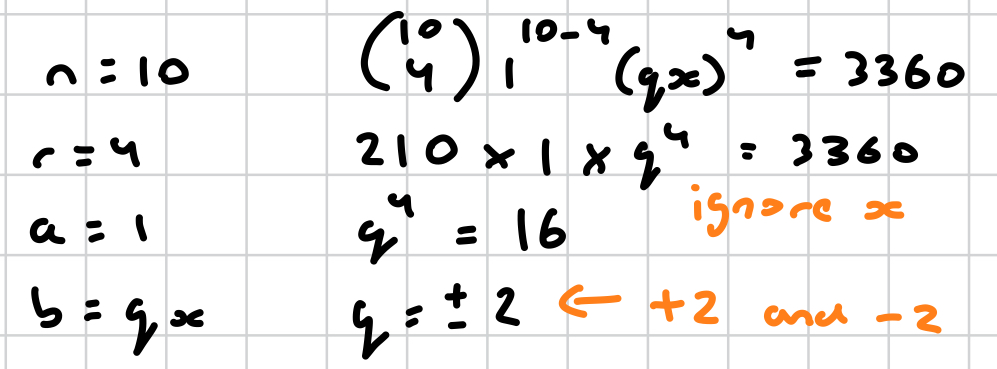
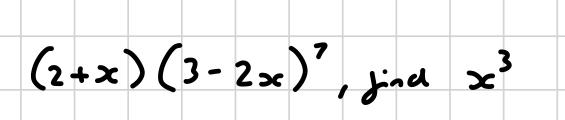
how do you solve this?

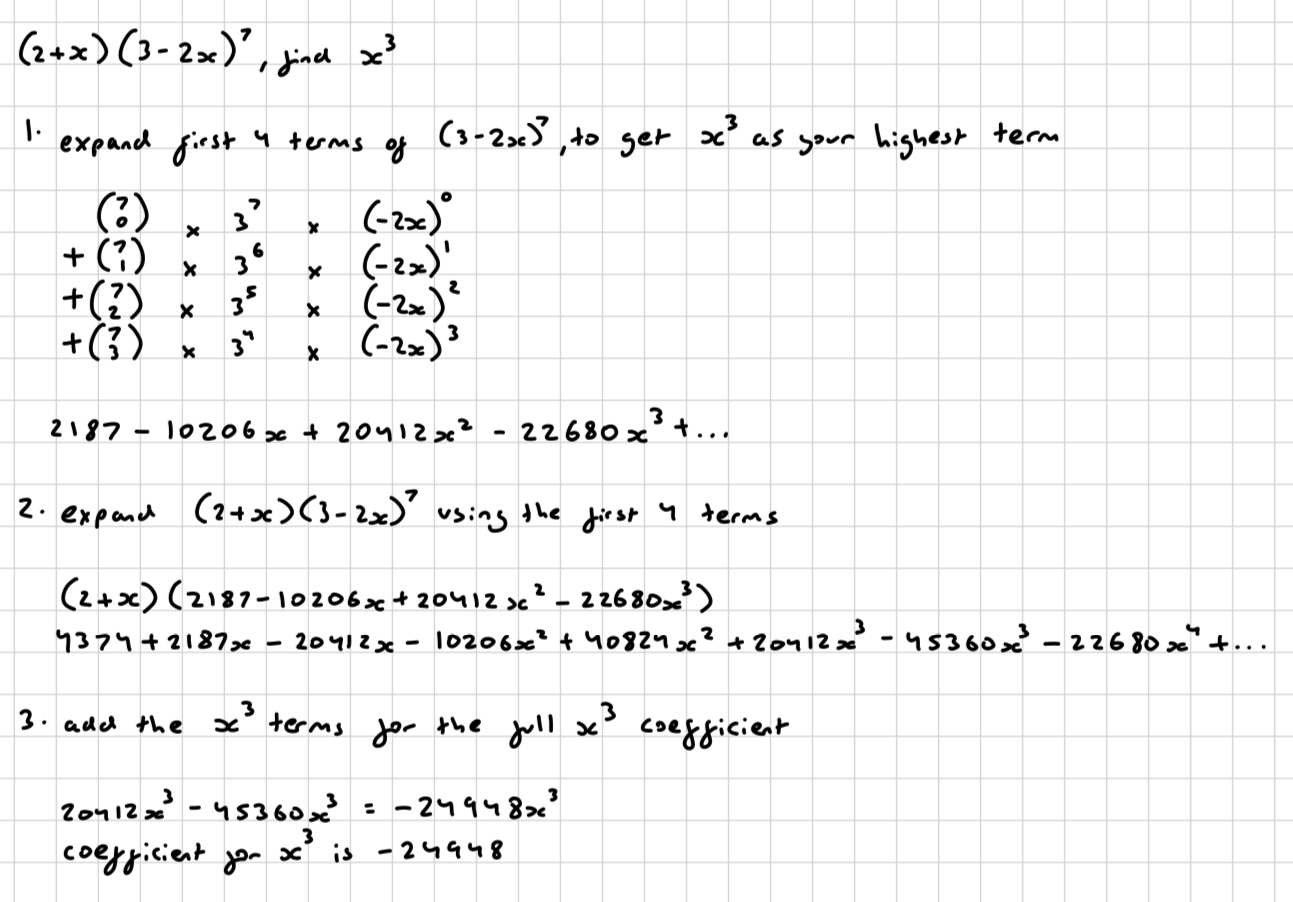
what is binomial estimation?

finding simple approximations for complicated functions

in binomial estimation, what happens when x < 1?

x^n gets smaller as n gets larger

in binomial expansion, what can you sometimes do when x is small? GET THIS EXPLAINED

ignore larger powers of x to approximate a function or estimate a value

if you’ve listed the first few terms of a sequence, how must you end the sequence?

+…

how do you solve this?

binomial expansion for n values that are not natural (i.e., negative or fractional values of n)

what does it mean for the expansion when n is a non-natural number?

binomial expansions are infinitely long, whereas when n is natural there is a definite number of terms

which values for n binomially expand into an infinite series and which have a definite number of terms?

natural numbers (positive, whole) - definite

non-natural numbers (negative, fractions) - infinite (as long as -1 < x < 1)

how should you answer questions on the binomial expansion for non-natural values of n?

1. since they produce an infinite series, the questions will ask ‘up until’

2. you answer up until x to the power of 1 less than the term they’ve asked for, because 1 counts as the first term (e.g., first four terms = 1, x, x², x³)

3. finish your sequences with ‘+…’

how do you solve this?

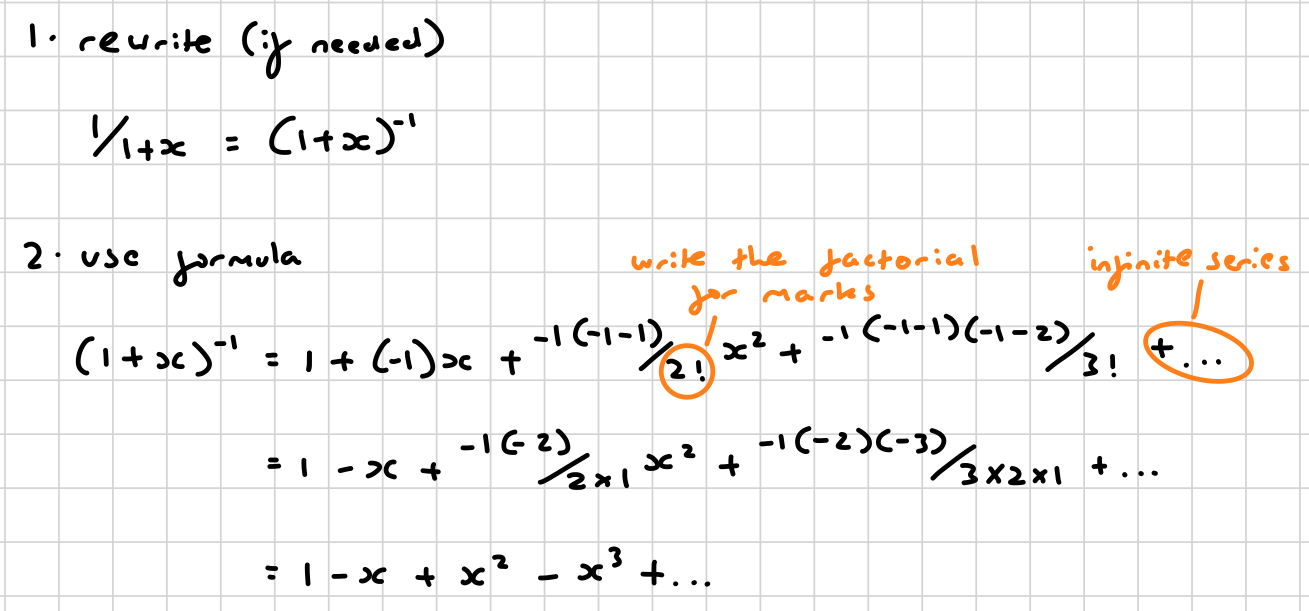
why are non-natural binomial expansions infinite?

because none of the factors in the expression equal zero

when are approximations based on the binomial expansion more accurate?

1. when more terms of the expansion are used

2. when the values of x substituted are closer to 0

when is the expansion for this term valid?

how do you expand (a + bx)^n ?

by using the binomial expansion of (1 + x)^n and taking a factor of a^n out of the expression

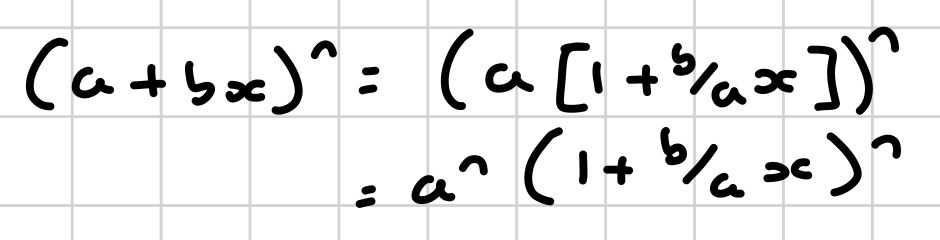
when is the expansion for (a + bx)^n , where n is a non-natural number, valid?

how do you solve this? ASK TEACHER ANOUT CONVERGENCE

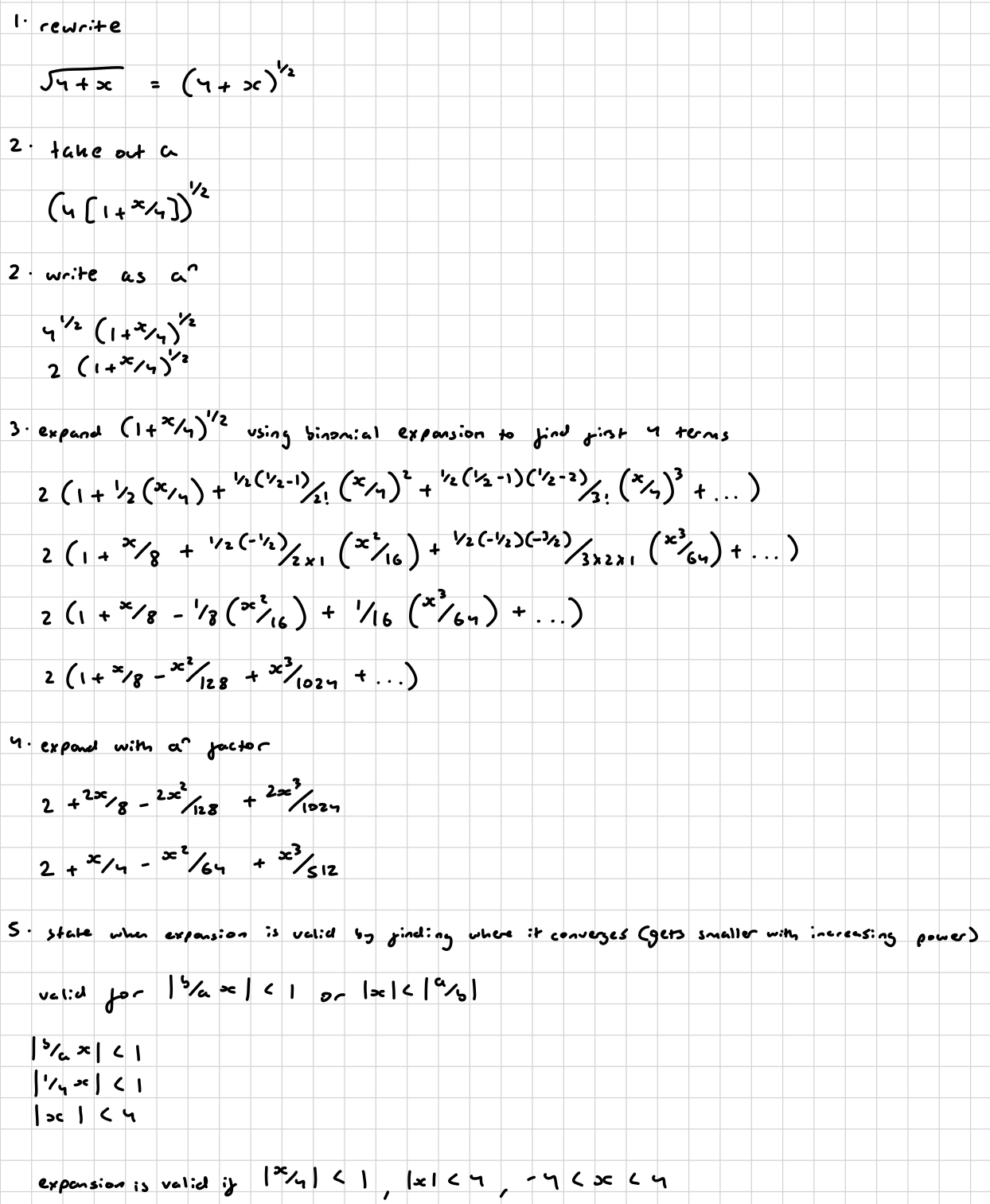
convergent and divergent series

convergent series - terms become smaller with increasing power (e.g., 8, 4, 2, 1, 1/2, 1/4, 1/8)

divergent series - terms become larger with increasing power (2, 4, 6, 8, 10, 12, 14)

which kind of series is binomial expansion only applicable for?

convergent series

what are the requirements for x in binomial expansion where n is non-natural? LOOK INTO THIS does this mean if it’s a fraction over 1 or negative below -1

?.?

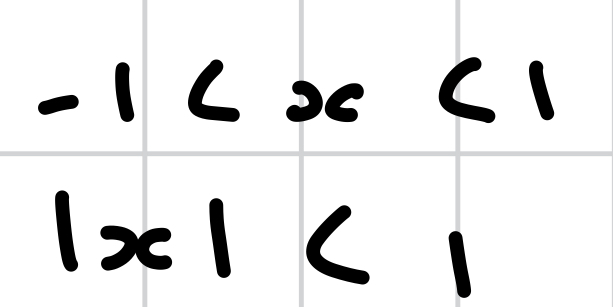
how do you solve this?

get back to this …

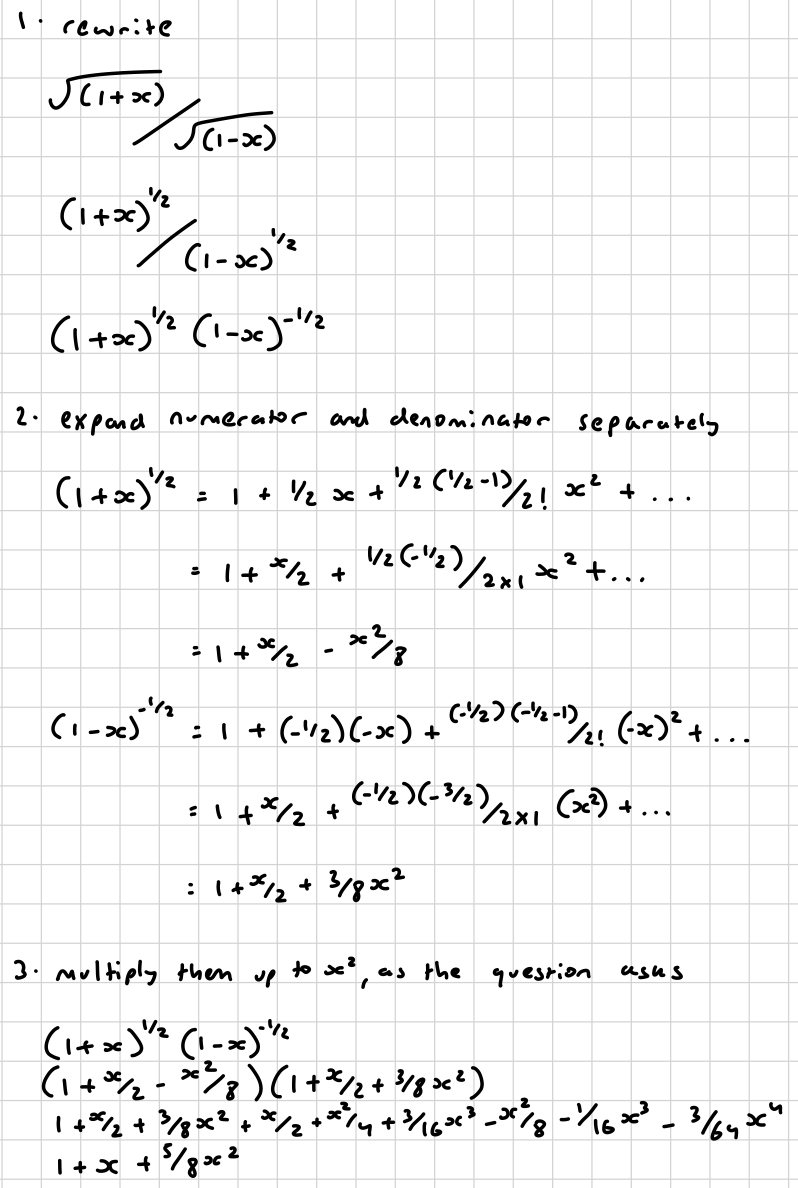
practice non natural pls ❤

how do you solve this?

using partial fractions

what’s important to remember about the b term?

the whole term is put to the power of, not just the x

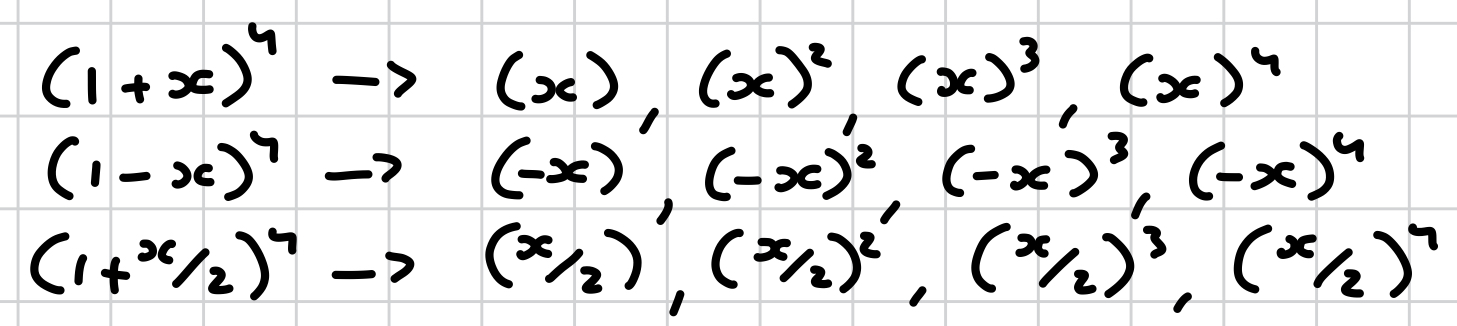
when do you include ‘+…’ at the end?

for infinite series, unless you have provided all the terms the question asked for

how do use a given value of x to find an approximation of a value?

1. write the bracket term with x = the given value

2. if x is applicable to find an approximation, the value should be decipherable from your answer

3. write that ‘the value can be estimated by substituting x = [ur x value] into the expansion, and [rearranging for the value alone; e.g., adding / multiplying]