Chapter 7 Toolbox

What is a ratio? How is it different from a proportion?

Ratios compare two number using division. For example, if I have 8 tabby cats and 3 black cats, the ratio of tabby to black cats is 8/3.

A proportion is two ratios set equal to each other. We can use proportions to find unknown quantaties.

What makes two polygons similar?

Similar polygons have the same shape but not the same size.

How do we write similarity statements?

We need to make sure that the order of vertices / sides are the same for each shape. So, for example, if angle A in one triangle and angle D in other other are the same, they need to be in the same spot in the statement.

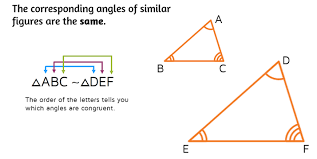
There are three ways we can prove triangles are similar. What are they?

Angle-angle: If two angles of a triangle are the same as two angles from another, the triangles are similar.

Side-Side-Side: If the corresponding side lengths of two triangles are proportional, the triangles are similar. (This means if each side of one triangle divided by its “partner” side in the other triangle is the same, the triangles are similar.)

Side-Angle-Side: If the lengths of two sides of one triangle are proportional to the corresponding sides of another triangle AND the angle between those two sides are congruent, the triangles are similar.

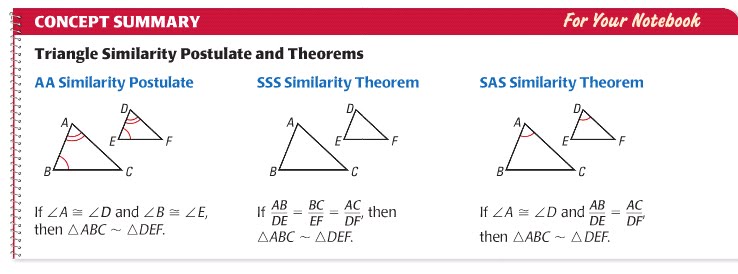
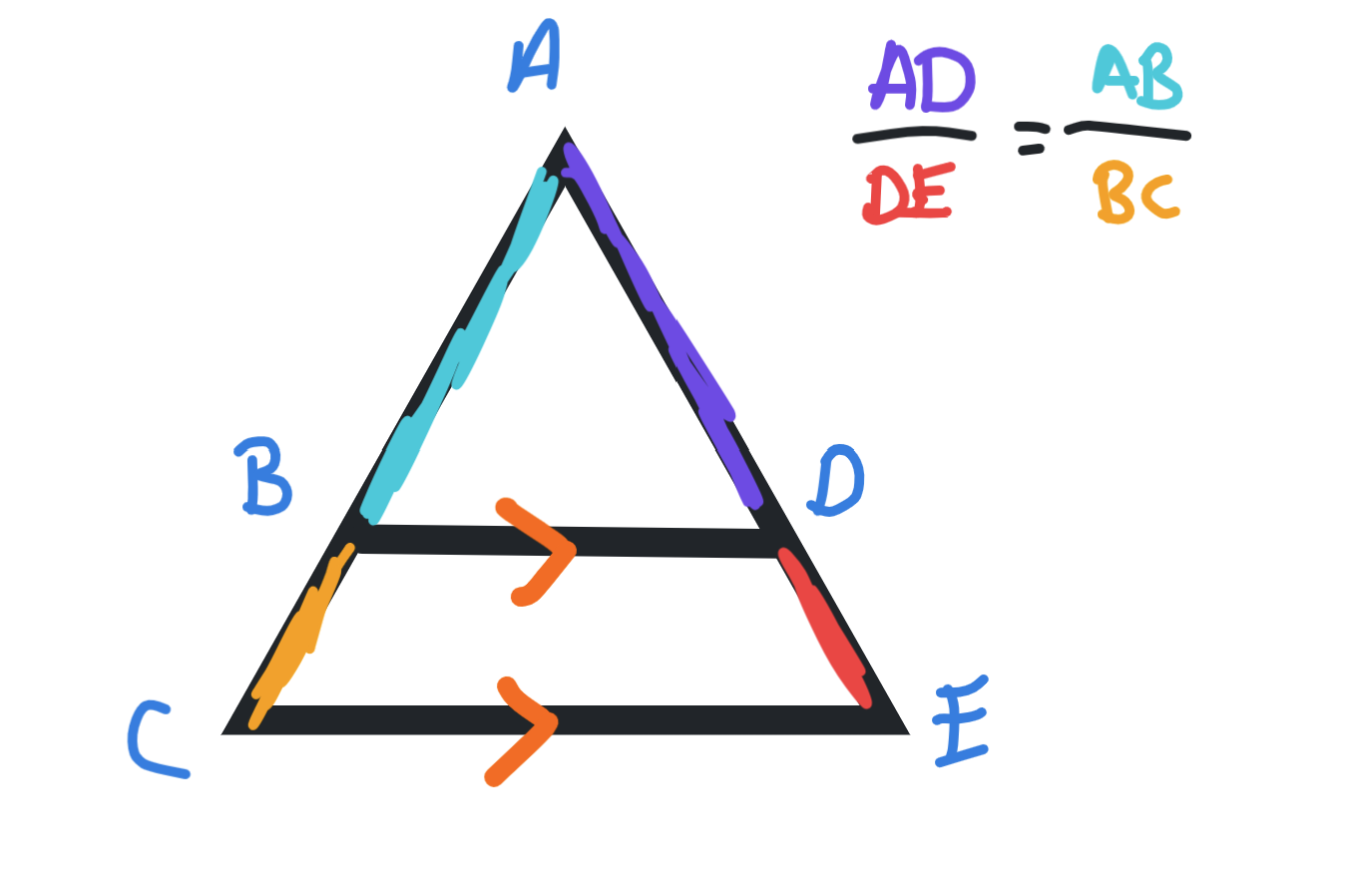
This triangle has two parallel lines. What do we know about this triangle?

We know the segments are proportional. In this case, (AD/DE) / (AB/BC)

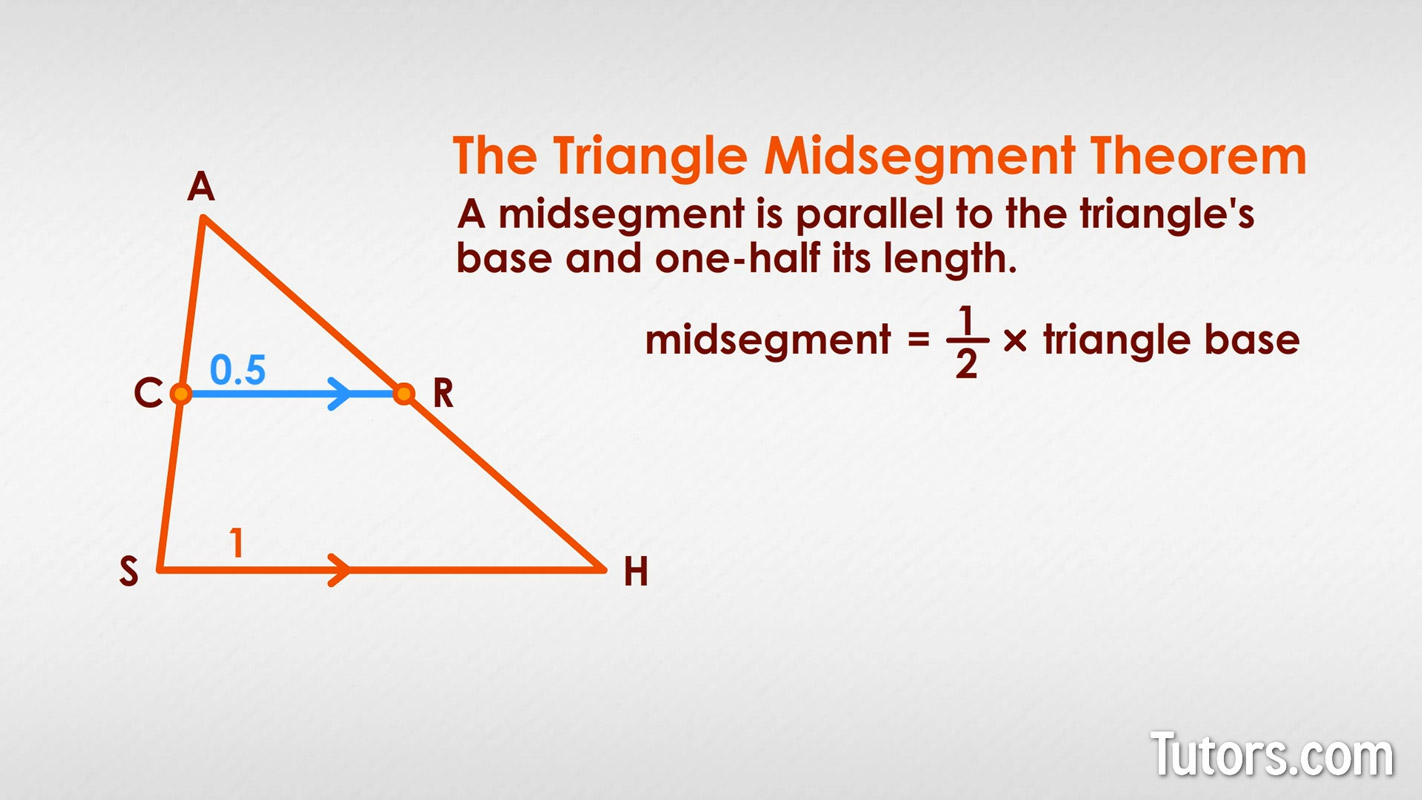
What is a midsegment? How many midsegments does a triangle have?

A midsegment is a segment with endpoints that are the midpoints of two sides of the triangle. Each triangle has three midpoints.

A triangle’s midpoint is half of it’s side.

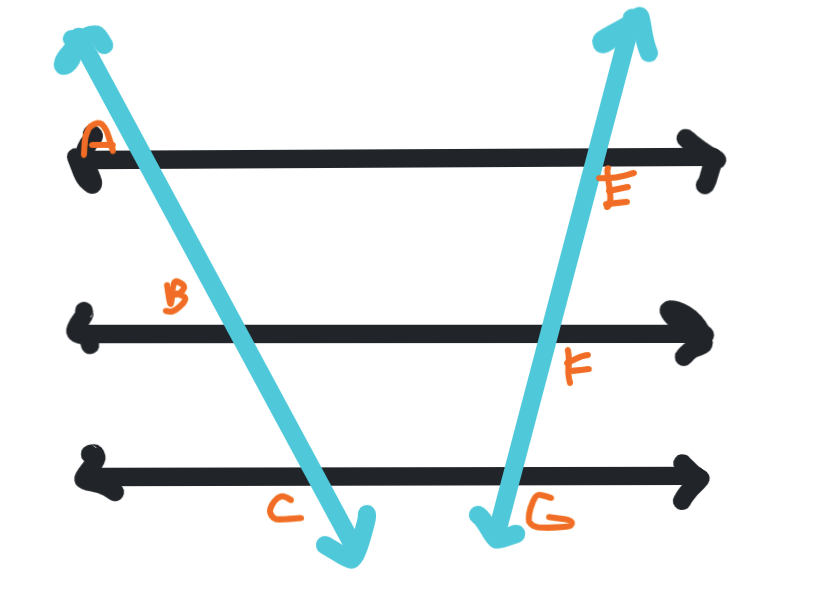
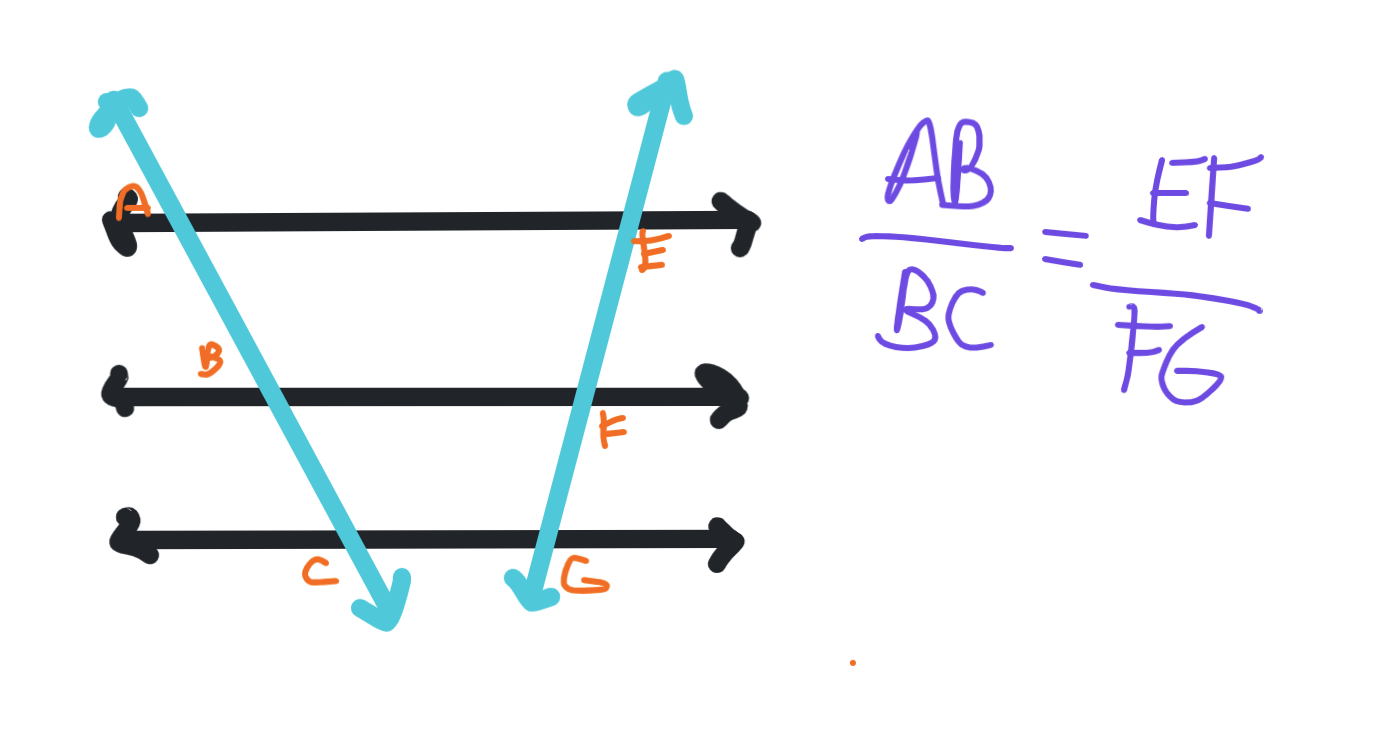
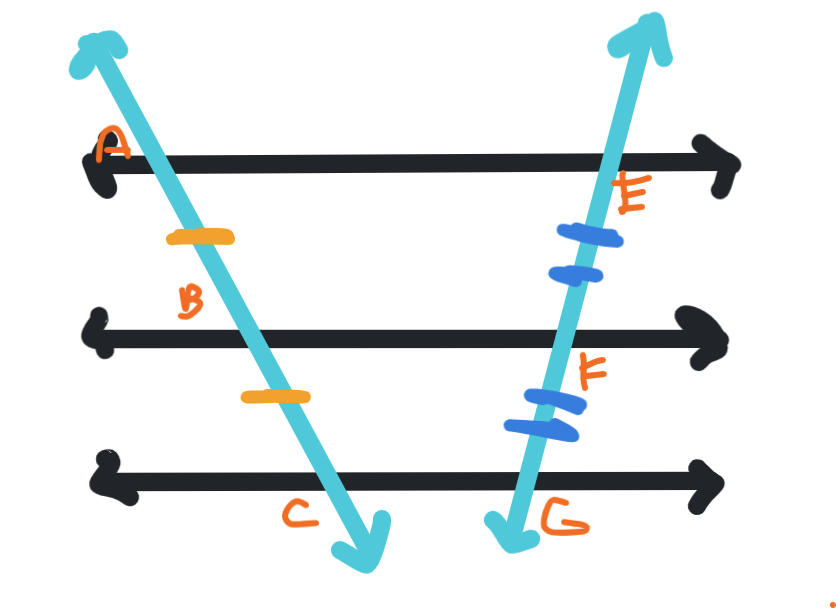
What do we know about this set of parallel lines?

The “cuts” of the transversals are proportionate. In this case, it means (AB/BC) = (EF/FG)

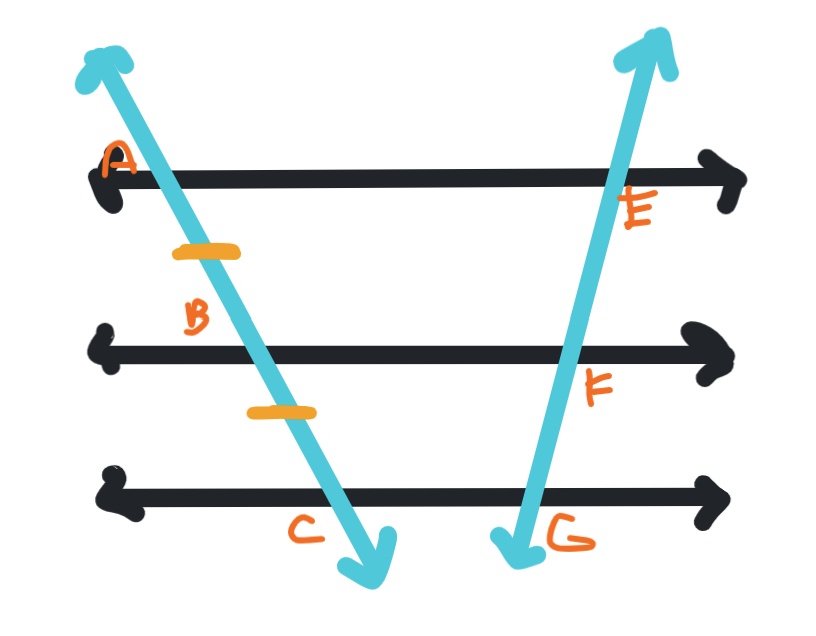
What do we know about this set of parallel lines?

The other parts of the transversal are also congruent to each other.

If two triangles are similar, what other “special segments” are similar?

The two triangles’ altitudes (lines drawn from vertex to the opposite side perpendicularly) are similar.

The two triangles’ angle bisectors (lines that split the vertex into two congruent angles) are similar.

The two triangles’ medians (lines drawn from the vertex to the midpoint of the opposite side) are similar.

This means that we can also include their ratios in the proportions that we set up. So it a ratio of two triangles’ sides reduces down to 1/3, so will the ratio of their altitudes, medians, and angle bisectors.

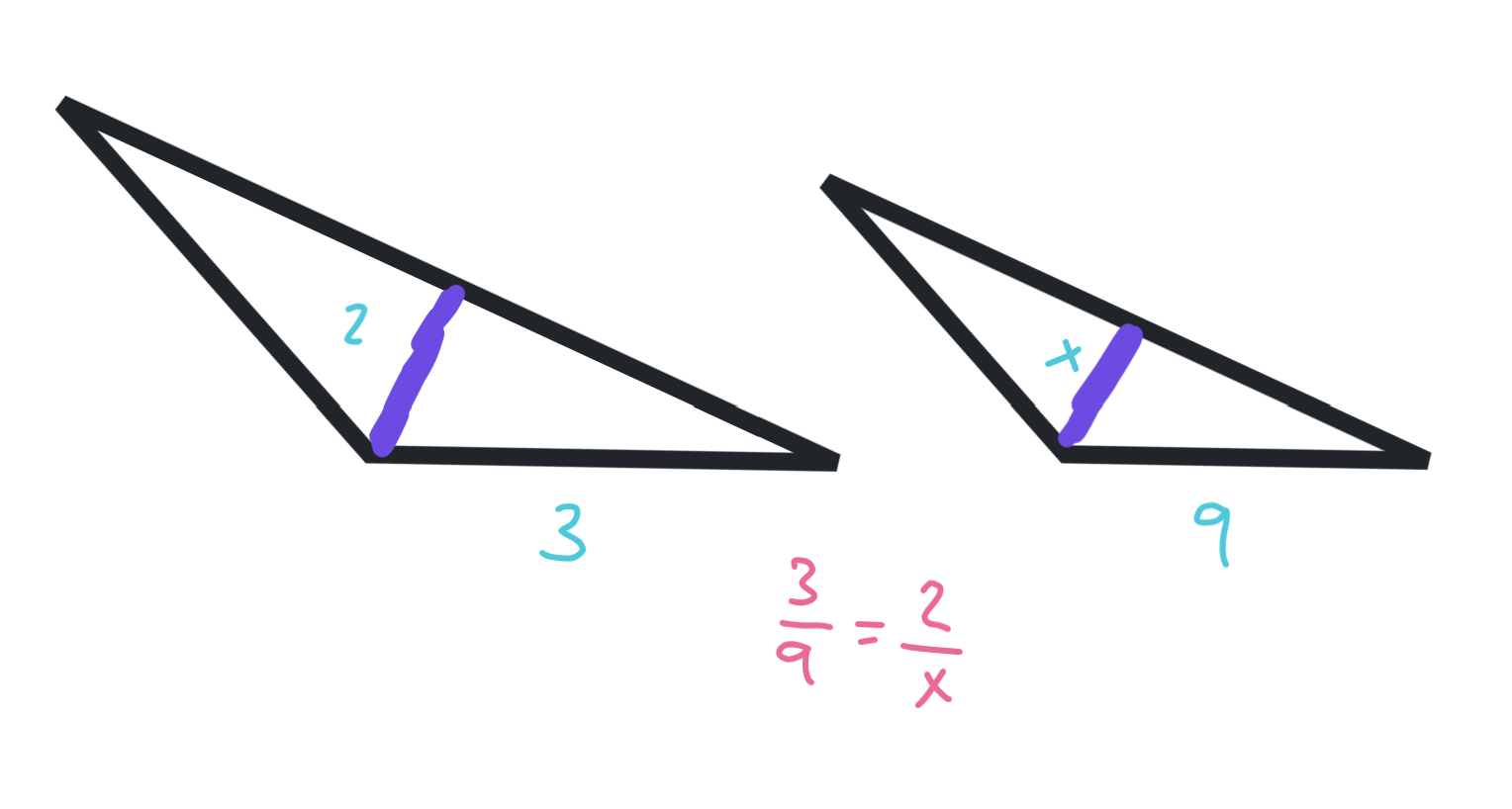
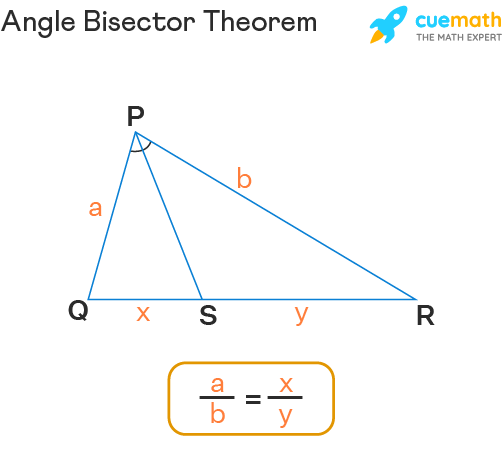
What is angle bisector theorem?

An angle bisector separates the side it bisect into segments that are proportional to the other two sides.

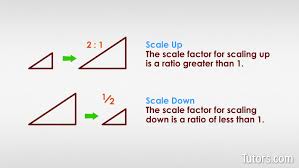
What is a scale factor?

A scale factor is the ratio of corresponding sides of two similar objects. For example, a scale factor of 2 means the new shape is double the size of the original. 

Interpret this scale factor: .4 in : 40 miles

How many miles does 1 in represent?

“Every .4 in on a map represents 40 miles in real life.

A full inch would represent 100 miles.