Chapter 6: Linear Momentum and Center of Mass

kinetic energy

In inelastic collisions, ________ is not conserved.

net external

However, momentum is conserved even when forces act at a distance as long as there are no ________ forces.

elastic collision

In a(n) ________, kinetic energy is conserved.

○ Common Error

________: The initial kinetic energy of the bullet can not be equated to the final energy stored in the spring because mechanical energy is not conserved during the collision; mechanical energy is conserved after the bullet lodges in the block.

uniform mass density

The object has ________ and a radius of r. Solution ● Symmetry about the y- axis dictates that the x- coordinate of the center of mass must be zero.

conservation of momentum

● Always use ________ when solving a collision problem and conservation of energy if the collision is elastic.

elastic collision

The angle between the paths of two balls of equal mass after a(n) ________ where one ball was initially at rest will always be 90°.

● Relationship between impulse and force

the impulse-momentum theorem

Example 6.1.1 Problem

During a collision with a wall lasting from t = 0 to t = 2 s, the force acting on a 2 kg object is given by the equation

Example 6.1.2 Problem

Compare a person falling on a bare gym floor with a person falling on a mat

Example 6.1.3 Problem

A bullet of mass 0.005 kg moving at a speed of 100 m/s lodges within a 1 kg block of wood resting on a frictionless surface and attached to a horizontal spring of k = 50 N/m

b) At this point, we have a standard mass and spring problem

○ A mass of 1.005 kg moves with an initial velocity of 0.5 m/s when the spring of k = 50 N/m is at its equilibrium position

○ Common Error

The initial kinetic energy of the bullet cannot be equated to the final energy stored in the spring because mechanical energy is not conserved during the collision; mechanical energy is conserved after the bullet lodges in the block

Example 6.1.4 Problem

A variable force F(t) acts on an object of mass m that is initially at rest for a time interval t. a) Find an expression for the final velocity by calculating the impulse and relating it to the momentum

Example 6.1.5 Problem

Particle C collides and sticks to particle S. If the particles have masses mC and mS and

● Inserting this into the second equation and solving via the quadratic equation yields two answers

v2 = −1 m/s and v2 = 1.769 m/s

This certainly makes sense

Everything is conserved between the initial situation and itself

● Thus, the second solution is the one we are interested in

The 10 kg mass has a final velocity of 1.769 m/s to the right

● Tip

Momentum is a vector

6.2

Center of Mass ● The center of mass is defined to be the weighted average of the location of mass in a system

Solution ● Computing the center of mass of a group of point masses is straightforward

simply plug into the above formulas

● Answer check

We note that each of these coordinates lies somewhere between the corresponding coordinates of the masses

○ This involves a common theme in Physics C

moving to a differential level

● Symmetry shortcut

Any plane of symmetry, mirror line, axis of rotation, or point of inversion must contain the center of mass

○ If you think of the center of mass as a weighted average, it makes sense

If there are identical mass distributions on either side of a plane, axis, or point, the weighted average must lie on that plane, axis, or point

Example 6.2.3 Problem

Calculate the center of mass of this object, with the center of the larger circle as the origin of your coordinate system

● This is an alternative derivation of the conservation of momentum for a system of particles

If the net force on a system of particles is zero, the total momentum of the system remains constant

\

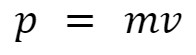
Momentum

Momentum

It obeys superposition such that the net momentum of a collection of objects is the vector sum of the momentum of each object

**Linear momentum**

A vector parallel to velocity

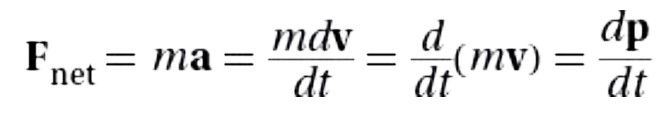
Relationship Between Force and Momentum

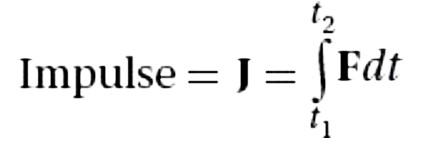
Definition of Impulse

**elastic collision**

In this collision, kinetic energy is conserved.

**inelastic collision**

In **this collision**, kinetic energy is not conserved.

**totally inelastic collision**

In this collision, kinetic energy is also not conserved, and the two objects remain stuck together after the collision.

center of mass

defined to be the weighted average of the location of mass in a system.

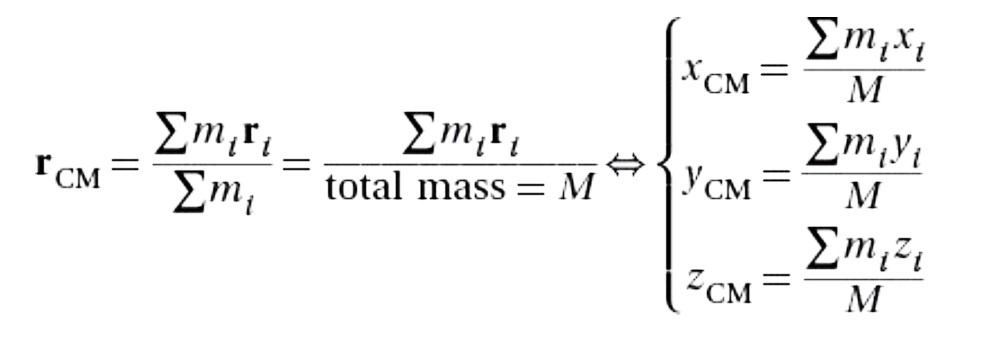
center of mass