Review- Chapter 7 Statistics

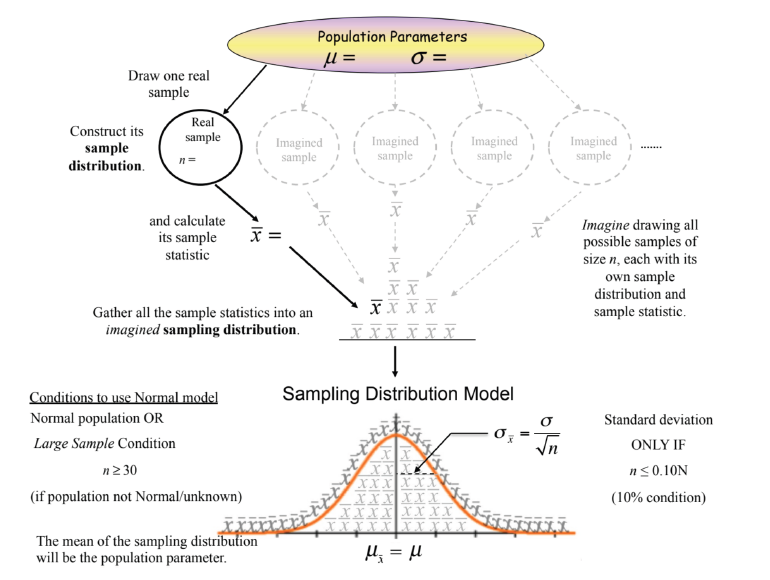
Sampling Distribution

• answers the question: HOW would my summary statistic behave if I could REPEAT the process of collecting data using a random sample?

• often approx. normal

• resonable likely outcomes: fall WITHIN 2 SE of the mean

  • middle 95%

• Describe: center, shape, spread

• does not show how the sample is distributed around the sample mean

• a distribution of sample means, not individual values of sample mean s

Rare event

• lie in the outer 5% of a sampling distrubtion

Unbiased estimator

• mean of a sampling distribution=population parameter →”unbiased estimator of the parameter”

• center is accurate

• mound shape, not skew

Good estimator

• unbiased and low variability

Standard Error (SE)

• the standard deviation of a sampling distribution

• increases for samples similar to the population

• decreases as n increases because n and o are inversely proportional σ_p̂ =√(p(1-p))/n, p̂ being the sample proportion

STEPS-approximate or simulated sampling distribution

1. Take a random sample of a FIXED size(n) from a population

2. compute a summary statistic

3. repeat steps (1, 2) many times

4. display the distribution of the summary statistic

*notation

Sampling distribution of the sample mean

• For ANY sample size(b), the sample mean is an unbiased estimator of the population mean

• the distribution of sample means becomes less spread as the sample size increases

• If a random sample of size n is selected from a distribution u and σ…

  • u_x̄ =u

  • σ_x̄ =σ/√n

Central Limit Theorem(CLT)

• Sampling distribution becomes MORE normal as the sample size gets larger

• The sampling distribution of mean is normal if conditions are met, even if the population shape is not normal or unknown

• Determines if outcomes are reasonably likely or not

• Implications

  • larger sample size(n) →narrower graph, more normal shape, less spread

  • the population can be ANY shape if n>= 30 → use a sample to model using approximately normal distribution

Conditions for mean

1. Independence assumption

2. randomization condition

3. 10% condition- the sample size is not more than 10% of the population

4. Large enough sample condition(n>30)

Conditions for proportion

*all same expect 4

4. large enough sample condition

• np>= 10 →at least 10 success

• n(1-p)>=10 →at least 10 failures

Sampling distribution of the SUM of a sample mean

• If a random sample of size n is selected from a distribution u and σ…

• u_sum=nu

• σ _sum=√nσ

Graphing - Sampling distribution of means

• Larger sample

  → more mound-shaped and “normal”

  → x axis less spread out

  • Max: skew left

  • min: skew right

  • median: narrow

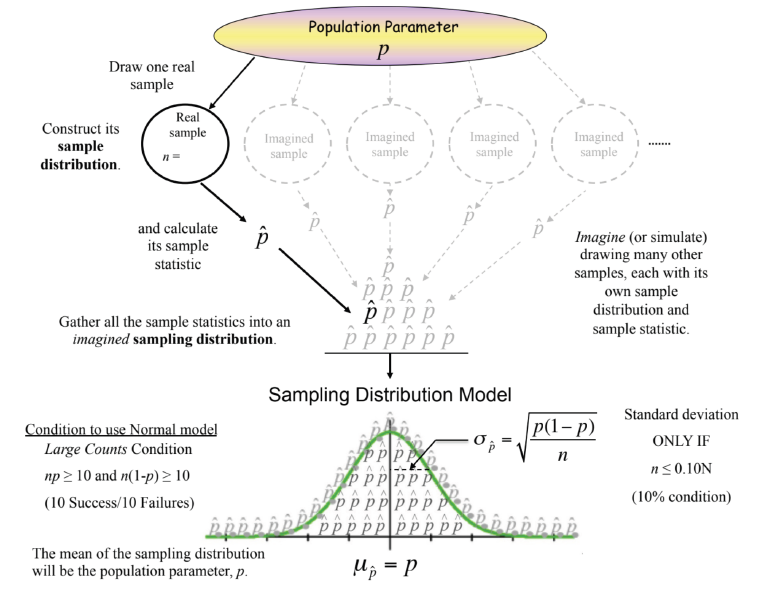
Sampling distribution of a sample proportion

• for any sample size(n), sample proportion=unbiased estimator for the population parameter

• distribution of sample proportions, less spread out as n increase

• CLT

• further p is from 0.5→ larger n required to achieve a normal approximation

*binomial experiment

• u_p̂=p, p being the population proportion

• σ_p̂ =√(p(1-p))/n, p̂ being the sample proportion

• for any size n, u_p̂ =unbiased estimator of p̂

• increasing n→ reduce variability and bias not related

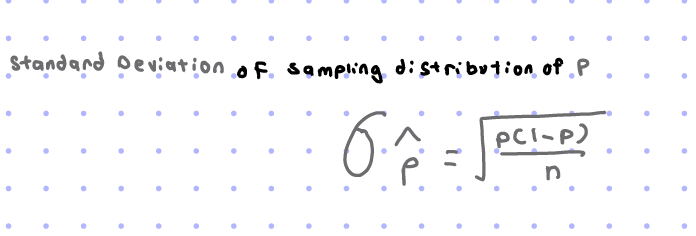
Sampling distribution of the SUM of a sample proportion

• u_sum=np

• σ _sum=√np(1-p) ← standard error

• σ _sum=np(1-p)← standard deviation

P

probability

• can draw a graph to show a middle center point for the sample proportion mean

• always symmetrical if p=0.5

• always unimodal(bc a binomial distribution)

n

Sample size

• larger sample size(n)

  →smaller spread in the sampling distribution

  → more it will show the distribution traits of the WHOLE population→ more like population graph

  → can or may not be more normal, depending on pop. graph

formula x=

x=u+-Zσ