WJEC AS Physics Unit 1.2 - Kinematics

Speed

Rate of change of distance. S=D/T. Unit=ms^-1

Average speed

Rate of change of distance calculated over a complete journey.

Mean speed=total distance travelled/total time

Unit;ms^-1

Instantaneous speed

Speed at a particular instant in time. Rate of change of distance.

Velocity

Rate of change of displacement. Unit; ms^-1

Mean velocity

Total displacement/total time taken. Unit; ms^-1

Instantaneous velocity

Rate of change of displacement at a particular instant in time.

Acceleration

Rate of change of velocity. Unit; ms^-2

Mean acceleration

Change in velocity/time taken. Unit: ms^-2

Instantaneous acceleration

The rate of change of velocity at a particular instant in time. Unit; ms^-2

Displacement

The shortest distance from A to B, together with the direction. Unit; m

Terminal velocity

The constant, maximum velocity of an object when the resistive forces on it are equal and opposite to the ‘accelerating’ force (e.g. pull of gravity)

Displacement-time graphs

• X-axis; time, t, in seconds

• Y-axis; displacement, x, in metres

• Steeper line = higher constant velocity

• Upwards; travelling at a constant positive speed/velocity

• Flat; stationary

• Downwards; negative velocity, going backwards

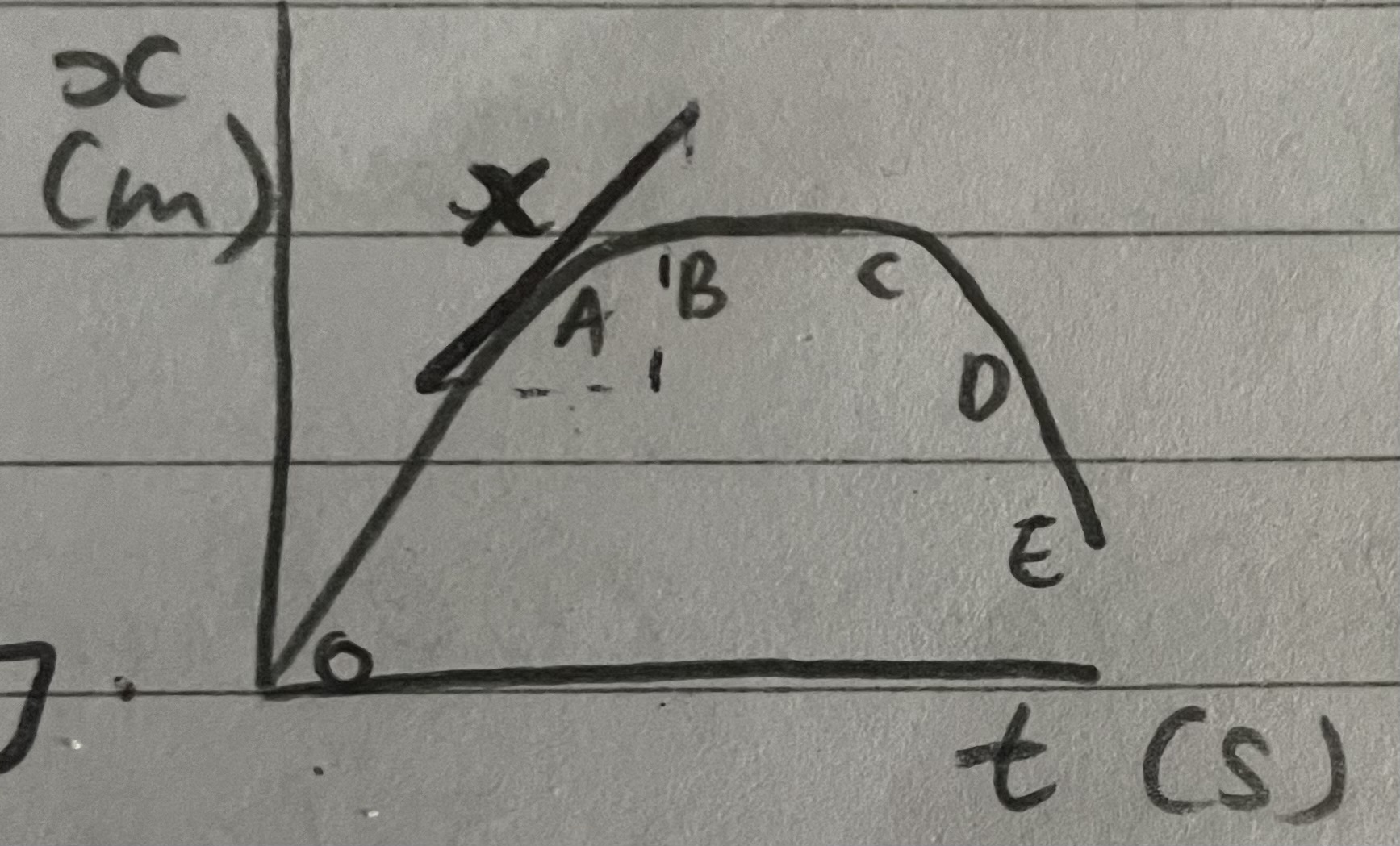
(Instantaneous) velocity from a displacement-time graph

Gradient of the tangent to the graph at the point

Average velocity from a displacement-time graph

Divide the change in displacement between the points by the time between them. (x/t)

Steep line on a displacement-time graph meaning

Higher constant velocity

Velocity-time graphs

• Gradient = acceleration

• Area under the graph = displacement travelled

• Negative velocity = travelling in the opposite direction to the original motion

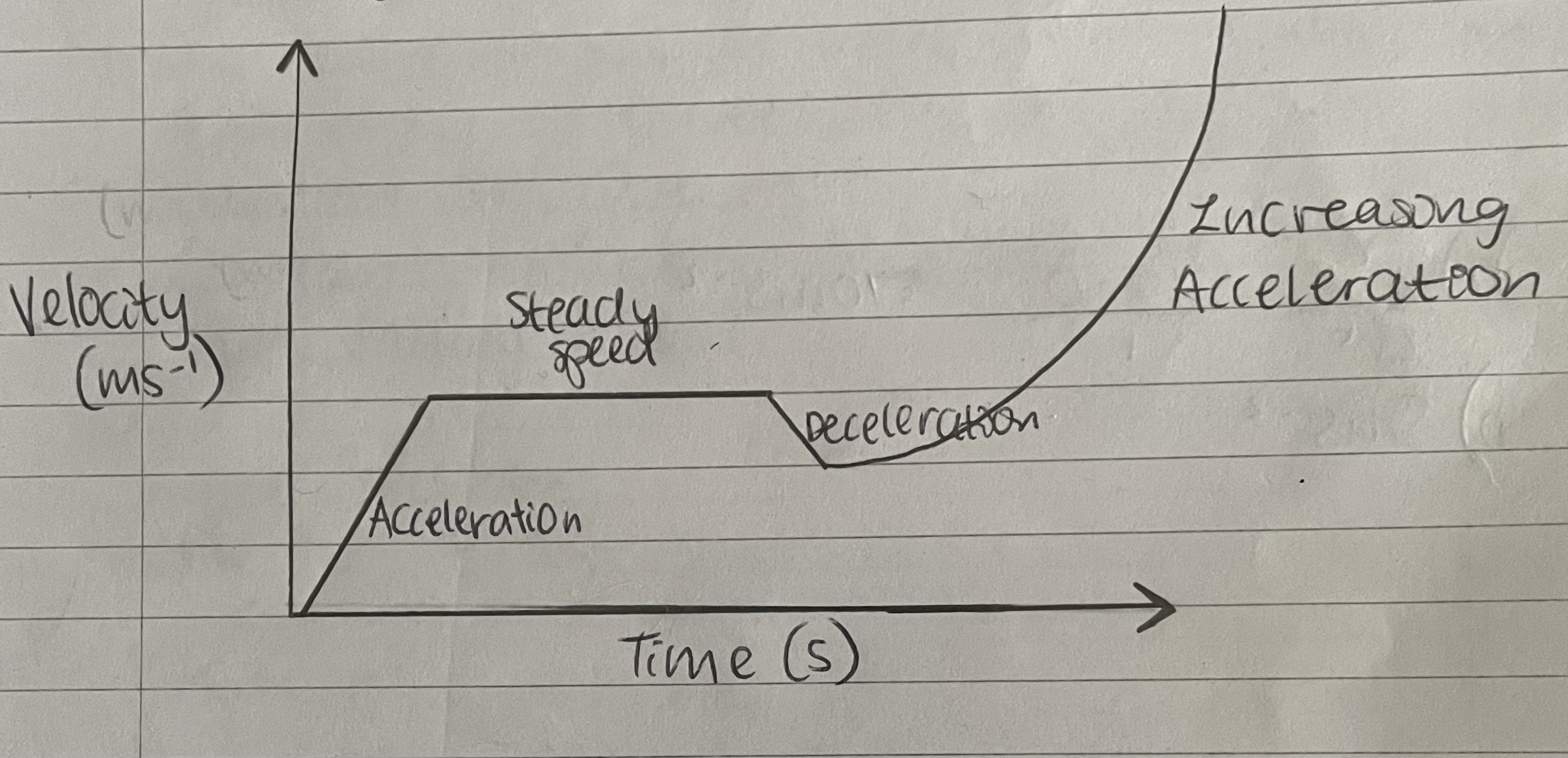
Distance travelled from a velocity-time graph with uniform motion

Area under the graph

Distance travelled from a velocity-time graph with non-uniform motion

Count the squares to estimate the distance travelled

Equations of uniform acceleration

• v=u+at

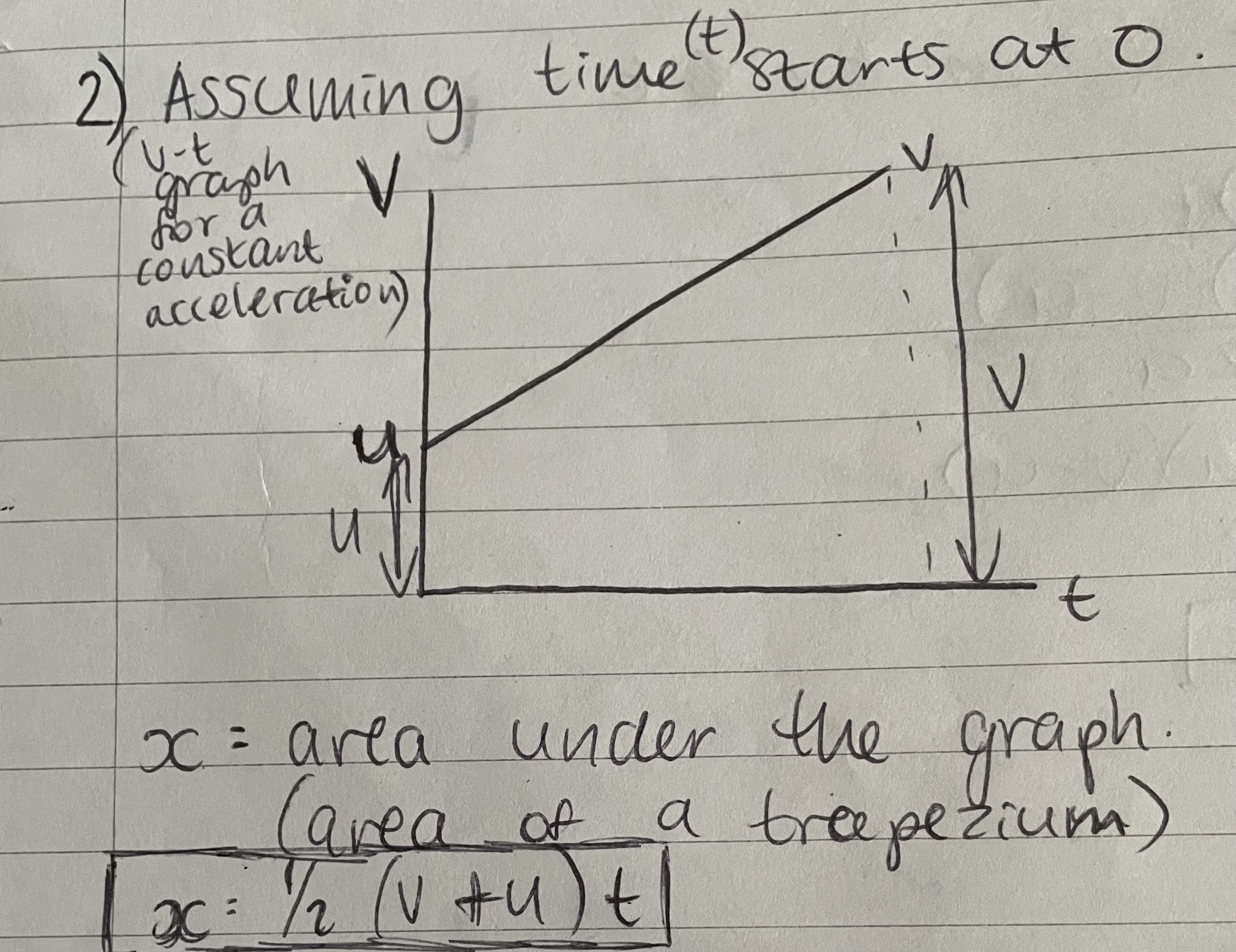
• x=1/2(v+u)t

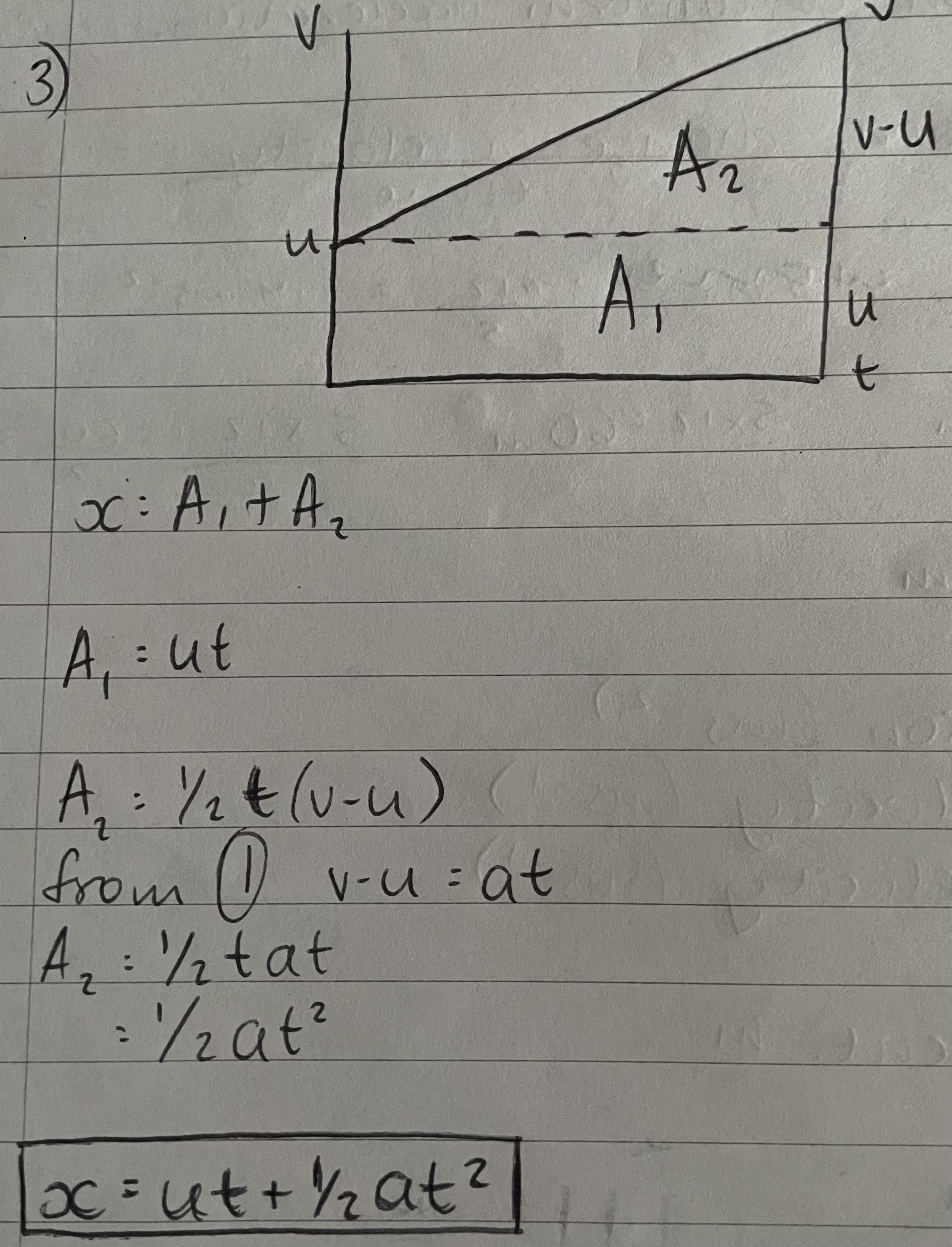
• x=ut+1/2at²

• v²=u²+2ax

  • a; acceleration (ms^-2)

  • u; initial velocity (ms^-1)

  • v; final velocity (ms^-1)

  • t; time (s)

  • x; displacement (m)

Deriving v=u+at

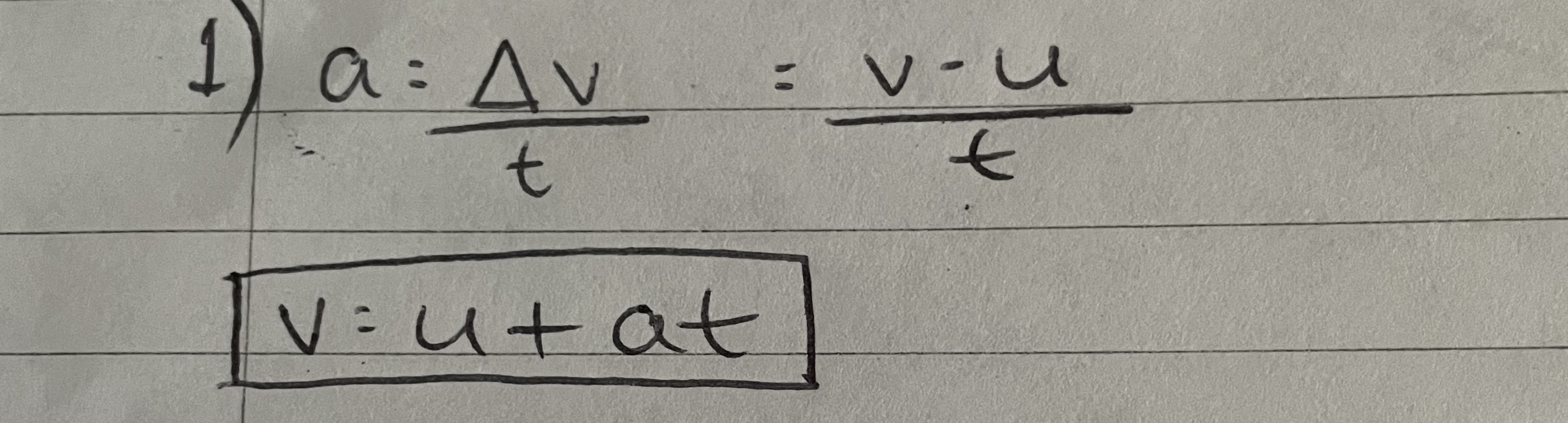
Deriving x=1/2(v+u)t

Deriving x=ut+1/2at²

Deriving v²=u²+2ax

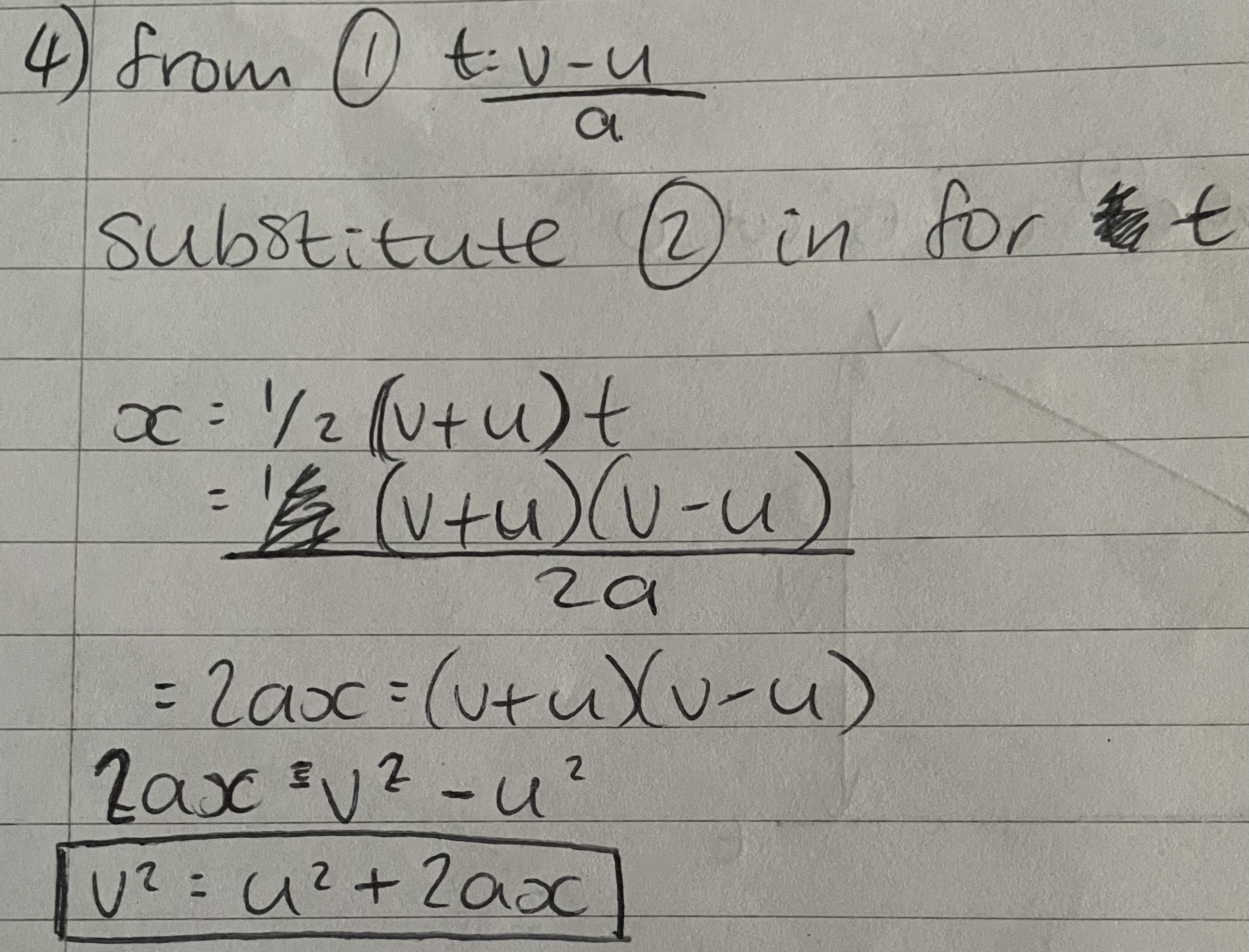
Terminal velocity

The constant, maximum velocity of an object when the resistive forces on it are equal and opposite to the ‘accelerating’ force (e.g. pull of gravity)

Projectiles

• use xuvat equations

• Vertical and horizontal motion of a body moving freely under gravity are independent (applies to projectile motion for objects being launched either horizontally or at an angle to the ground)

• At an angle to the ground;

  • Vertical velocity will change due to the acceleration of free fall

  • The vertical component will depend on the initial velocity where v_vertical=v sinθ

  • The horizontal component will also depend on the initial velocity, where v_horizontal = v cosθ

  • Constant horizontal component, horizontal acceleration = g cos 90 =0

  • Vertical velocity will change fur to accelerator of free fall

  • Assume air resistance is 0