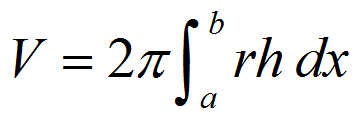AP Calc Exam Review
0.0(0)
Card Sorting
1/152
Earn XP
Description and Tags
Study Analytics
Name | Mastery | Learn | Test | Matching | Spaced |
|---|
No study sessions yet.
153 Terms
1
New cards
Intermediate Value Theorem
If f(1)\=-4 and f(6)\=9, then there must be a x-value between 1 and 6 where f crosses the x-axis.
2
New cards
Average Rate of Change
Slope of secant line between two points, use to estimate instantanous rate of change at a point.
3
New cards
Instantenous Rate of Change
Slope of tangent line at a point, value of derivative at a point
4
New cards
Formal definition of derivative
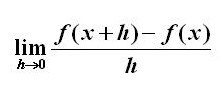
5
New cards
Alternate definition of derivative
limit as x approaches a of [f(x)-f(a)]/(x-a)
6
New cards
When f '(x) is positive, f(x) is
increasing
7
New cards
When f '(x) is negative, f(x) is
decreasing
8
New cards
When f '(x) changes from negative to positive, f(x) has a
relative minimum
9
New cards
When f '(x) changes from positive to negative, f(x) has a
relative maximum
10
New cards
When f '(x) is increasing, f(x) is
concave up
11
New cards
When f '(x) is decreasing, f(x) is
concave down
12
New cards
When f '(x) changes from increasing to decreasing or decreasing to increasing, f(x) has a
point of inflection
13
New cards
When is a function not differentiable
corner, cusp, vertical tangent, discontinuity
14
New cards
Product Rule
uv' + vu'
15
New cards
Quotient Rule
(uv'-vu')/v²
16
New cards
Chain Rule
f '(g(x)) g'(x)
17
New cards
y \= x cos(x), state rule used to find derivative
product rule
18
New cards
y \= ln(x)/x², state rule used to find derivative
quotient rule
19
New cards
y \= cos²(3x)
chain rule
20
New cards
Particle is moving to the right/up
velocity is positive
21
New cards
Particle is moving to the left/down
velocity is negative
22
New cards
absolute value of velocity
speed
23
New cards
y \= sin(x), y' \=
y' \= cos(x)
24
New cards
y \= cos(x), y' \=
y' \= -sin(x)
25
New cards
y \= tan(x), y' \=
y' \= sec²(x)
26
New cards
y \= csc(x), y' \=
y' \= -csc(x)cot(x)
27
New cards
y \= sec(x), y' \=
y' \= sec(x)tan(x)
28
New cards
y \= cot(x), y' \=
y' \= -csc²(x)
29
New cards
y \= sin⁻¹(x), y' \=
y' \= 1/√(1 - x²)
30
New cards
y \= cos⁻¹(x), y' \=
y' \= -1/√(1 - x²)
31
New cards
y \= tan⁻¹(x), y' \=
y' \= 1/(1 + x²)
32
New cards
y \= cot⁻¹(x), y' \=
y' \= -1/(1 + x²)
33
New cards
y \= e^x, y' \=
y' \= e^x
34
New cards
y \= a^x, y' \=
y' \= a^x ln(a)
35
New cards
y \= ln(x), y' \=
y' \= 1/x
36
New cards
y \= log (base a) x, y' \=
y' \= 1/(x lna)
37
New cards
To find absolute maximum on closed interval [a, b], you must consider...
critical points and endpoints
38
New cards
mean value theorem
if f(x) is continuous and differentiable, slope of tangent line equals slope of secant line at least once in the interval (a, b)
f '(c) = \[f(b) - f(a)\]/(b - a)
f '(c) = \[f(b) - f(a)\]/(b - a)
39
New cards
If f '(x) \= 0 and f"(x) \> 0,
f(x) has a relative minimum
40
New cards
If f '(x) \= 0 and f"(x) < 0,
f(x) has a relative maximum
41
New cards
Linearization
use tangent line to approximate values of the function
42
New cards
rate
derivative
43
New cards
left riemann sum
use rectangles with left-endpoints to evaluate integral (estimate area)
44
New cards
right riemann sum
use rectangles with right-endpoints to evaluate integrals (estimate area)
45
New cards
trapezoidal rule
use trapezoids to evaluate integrals (estimate area)
46
New cards
\[(h1 - h2)/2]*base
area of trapezoid
47
New cards
definite integral
has limits a & b, find antiderivative, F(b) - F(a)
48
New cards
indefinite integral
no limits, find antiderivative + C, use inital value to find C
49
New cards
area under a curve
∫ f(x) dx integrate over interval a to b
50
New cards
area above x-axis is
positive
51
New cards
area below x-axis is
negative
52
New cards
average value of f(x)
\= 1/(b-a) ∫ f(x) dx on interval a to b
53
New cards
If g(x) \= ∫ f(t) dt on interval 2 to x, then g'(x) \=
g'(x) \= f(x)
54
New cards
Fundamental Theorem of Calculus
∫ f(x) dx on interval a to b \= F(b) - F(a)
55
New cards
To find particular solution to differential equation, dy/dx \= x/y
separate variables, integrate + C, use initial condition to find C, solve for y
56
New cards
To draw a slope field,
plug (x,y) coordinates into differential equation, draw short segments representing slope at each point
57
New cards
slope of horizontal line
zero
58
New cards
slope of vertical line
undefined
59
New cards
methods of integration
substitution, parts, partial fractions
60
New cards
use substitution to integrate when
a function and it's derivative are in the integrand
61
New cards
use integration by parts when
two different types of functions are multiplied
62
New cards
∫ u dv \=
uv - ∫ v du
63
New cards
use partial fractions to integrate when
integrand is a rational function with a factorable denominator
64
New cards
dP/dt \= kP(M - P)
logistic differential equation, M \= carrying capacity
65
New cards
P \= M / (1 + Ae^(-Mkt))
logistic growth equation
66
New cards
given rate equation, R(t) and inital condition when t = a, R(t) = y₁ find final value when t = b
y₁ + Δy = y
Δy = ∫ R(t) over interval a to b
Δy = ∫ R(t) over interval a to b
67
New cards
given v(t) and initial position t \= a, find final position when t \= b
s₁+ Δs = s
Δs = ∫ v(t) over interval a to b
Δs = ∫ v(t) over interval a to b
68
New cards
given v(t) find displacement
∫ v(t) over interval a to b
69
New cards
given v(t) find total distance travelled
∫ abs[v(t)] over interval a to b
70
New cards
area between two curves
∫ f(x) - g(x) over interval a to b, where f(x) is top function and g(x) is bottom function
71
New cards
volume of solid with base in the plane and given cross-section
∫ A(x) dx over interval a to b, where A(x) is the area of the given cross-section in terms of x
72
New cards
volume of solid of revolution - no washer
π ∫ r² dx over interval a to b, where r \= distance from curve to axis of revolution
73
New cards
volume of solid of revolution - washer
π ∫ R² - r² dx over interval a to b, where R \= distance from outside curve to axis of revolution, r \= distance from inside curve to axis of revolution
74
New cards
length of curve
∫ √(1 + (dy/dx)²) dx over interval a to b
75
New cards
L'Hopitals rule
use to find indeterminate limits, find derivative of numerator and denominator separately then evaluate limit
76
New cards
indeterminate forms
0/0, ∞/∞, ∞*0, ∞ - ∞, 1^∞, 0⁰, ∞⁰
77
New cards
6th degree Taylor Polynomial
polynomial with finite number of terms, largest exponent is 6, find all derivatives up to the 6th derivative
78
New cards
Taylor series
polynomial with infinite number of terms, includes general term
79
New cards
nth term test
if terms grow without bound, series diverges
80
New cards
alternating series test
lim as n approaches zero of general term \= 0 and terms decrease, series converges
81
New cards
converges absolutely
alternating series converges and general term converges with another test
82
New cards
converges conditionally
alternating series converges and general term diverges with another test
83
New cards
ratio test
lim as n approaches ∞ of ratio of (n+1) term/nth term \> 1, series converges
84
New cards
find interval of convergence
use ratio test, set \> 1 and solve absolute value equations, check endpoints
85
New cards
find radius of convergence
use ratio test, set \> 1 and solve absolute value equations, radius \= center - endpoint
86
New cards
integral test
if integral converges, series converges
87
New cards
limit comparison test
if lim as n approaches ∞ of ratio of comparison series/general term is positive and finite, then series behaves like comparison series
88
New cards
geometric series test
general term \= a₁r^n, converges if -1 < r < 1
89
New cards
p-series test
general term \= 1/n^p, converges if p \> 1
90
New cards
derivative of parametrically defined curve x(t) and y(t)
dy/dx = dy/dt / dx/dt
91
New cards
second derivative of parametrically defined curve
find first derivative, dy/dx \= dy/dt / dx/dt, then find derivative of first derivative, then divide by dx/dt
92
New cards
length of parametric curve
∫ √ (dx/dt)² + (dy/dt)² over interval from a to b
93
New cards
given velocity vectors dx/dt and dy/dt, find speed
√(dx/dt)² + (dy/dt)² not an integral!
94
New cards
given velocity vectors dx/dt and dy/dt, find total distance travelled
∫ √ (dx/dt)² + (dy/dt)² over interval from a to b
95
New cards
area inside polar curve
1/2 ∫ r² over interval from a to b, find a & b by setting r \= 0, solve for theta
96
New cards
area inside one polar curve and outside another polar curve
1/2 ∫ R² - r² over interval from a to b, find a & b by setting equations equal, solve for theta.
97
New cards
Product rule Derivatives
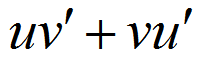
98
New cards
Volume of Disc
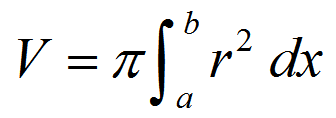
99
New cards
Volume of Washer
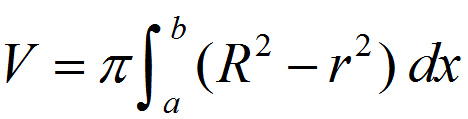
100
New cards
Volume of Shell